Тема: Двойственный симплексный метод

Двойственный симплексный используется для решения задачи линейного программирования, записанной в форме основной задачи, среди векторов которой имеется m единичных, свободные члены b_i принимают любые значения, а система ограничений задана в виде неравенств смысла «≥», либо смешанных неравенств «≥», «≤» и «=».

Если в симплексном методе оптимальный план получается в результате перехода от одного опорного плана к другому, то в двойственном симплексном методе – в результате движения по псевдопланам.

Определение 1. Условно-отимальным планом или псевдопланом называется план, в котором удовлетворяется признак оптимальности (все коэффициенты индексной строки ∆_j ≥ 0 при решении задачи на максимум и все ∆_j ≤ 0 при решении задачи на минимум целевой функции), а среди значений столбца свободных членов b_i имеются отрицательные числа.

Алгоритм двойственного симплексного метода включает следующие этапы:

1. Составление псевдоплана.

Систему ограничений исходной задачи приводим к системе неравенств смысла «≥». Для этого обе части неравенств смысла «≥» умножаем на (−1). Если ограничение исходной задачи задано в виде равенства, необходимо представить его в виде системы двух неравенств противоположного смысла.

От полученной системы неравенств смысла «≤» переходим к системе уравнений, вводя неотрицательные дополнительные переменные, которые становятся базисными. Разрешаем систему уравнений относительно базисных переменных и первый опорный план заносим в симплексную таблицу. Индексную строку таблицы заполняем коэффициентами целевой функции, взятыми с противоположными знаками.

2. Проверка плана на оптимальность.

Если в полученном опорном плане условие оптимальности не выполняется, то осуществляем симплексную процедуру(см.решение задачи ЛП симплексным методом). В этом случае существует следующее правило: при расчете значений столбца q отрицательные значения свободных членов b_i делим только на отрицательные коэффициенты направляющего столбца, положительные значения b_i - на положительные коэффициенты a_ik, а в строке, имеющей разноименные знаки b_i и a_ik значения q_i не существует.

Если в опорном плане условие оптимальности удовлетворяется и все значения столбца свободных членов b_i ≥ 0, то получен оптимальный план. Наличие среди столбца свободных членов хотя бы одного отрицательного числа свидетельствует о получении псевдоплана и требует перехода к следующему этапу алгоритма.

3. Определение направляющих (разрешающих) строки и столбца.

Среди отрицательных значений столбца свободных членов b_i выбираем наибольшее по абсолютной величине. Строка, соответствующая этому значению, является направляющей ( i = k ).

Симплексную таблицу дополняем строкой q, в которую заносим результаты деления, взятые по абсолютной величине, коэффициентов индексной строки на соответствующие отрицательные коэффициенты направляющей строки. В столбцах, имеющих значения a_ik ≥ 0, q_j не существует. Столбец с минимальным значением q_j является направляющим. Разрешающий элемент, находящийся на пересечении направляющих строки и столбца симплексной таблицы, в двойственном симплексном методе он всегда отрицательный.

4. Определение нового опорного плана.

Новый опорный план получаем в результате пересчета симплексной таблицы методом Жордана-Гаусса и далее переходим к этапу 2 алгоритма.

Решение задачи продолжаем до получения оптимального плана.

Если все коэффициенты направляющей строки положительны, т.е. a_ik ≥ 0, то задача не имеет решения, так как в этом случае q_j , ( 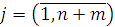не существует.

Пример.

Определить 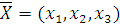, который удовлетворяет условиям

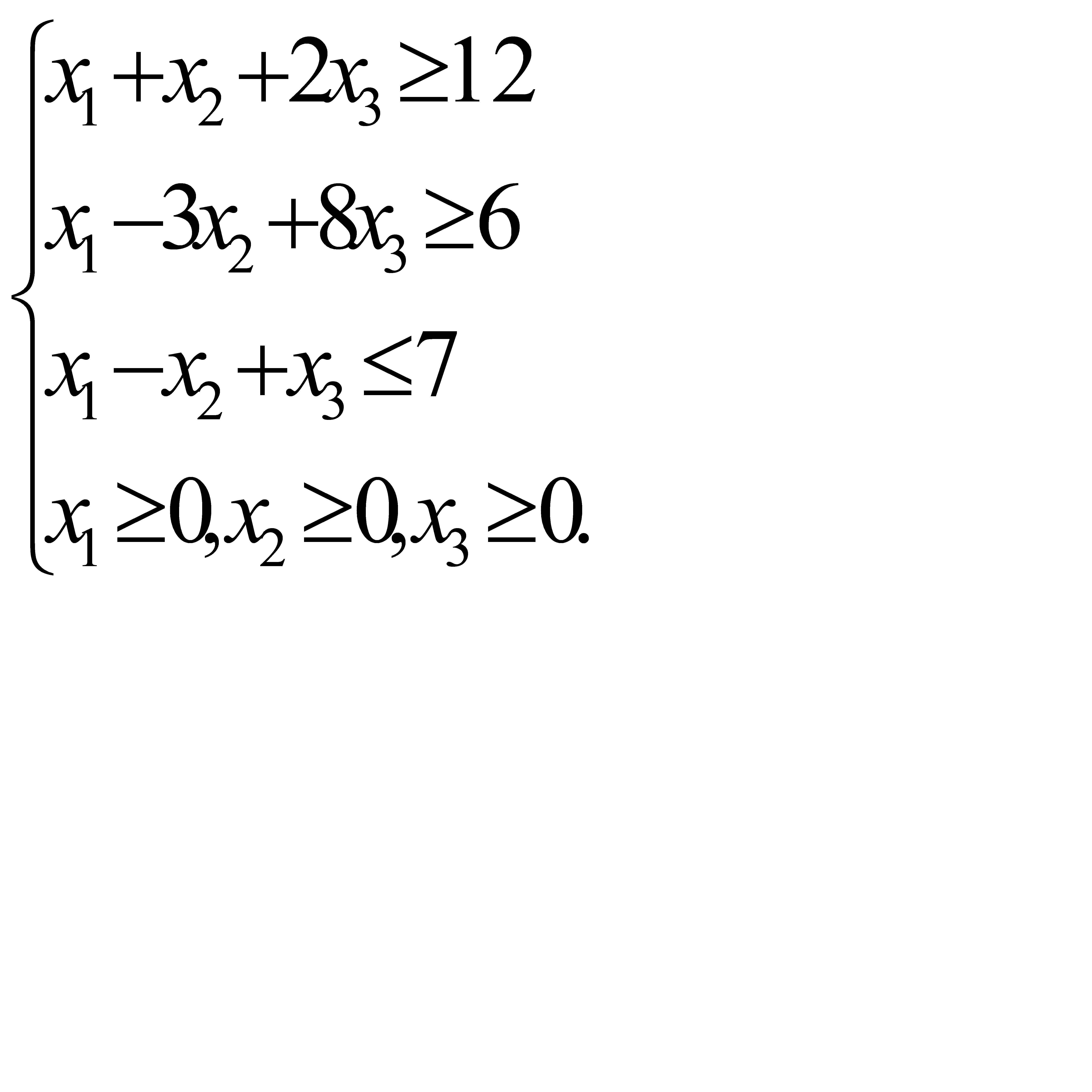
и доставляет максимальное значение целевой функции

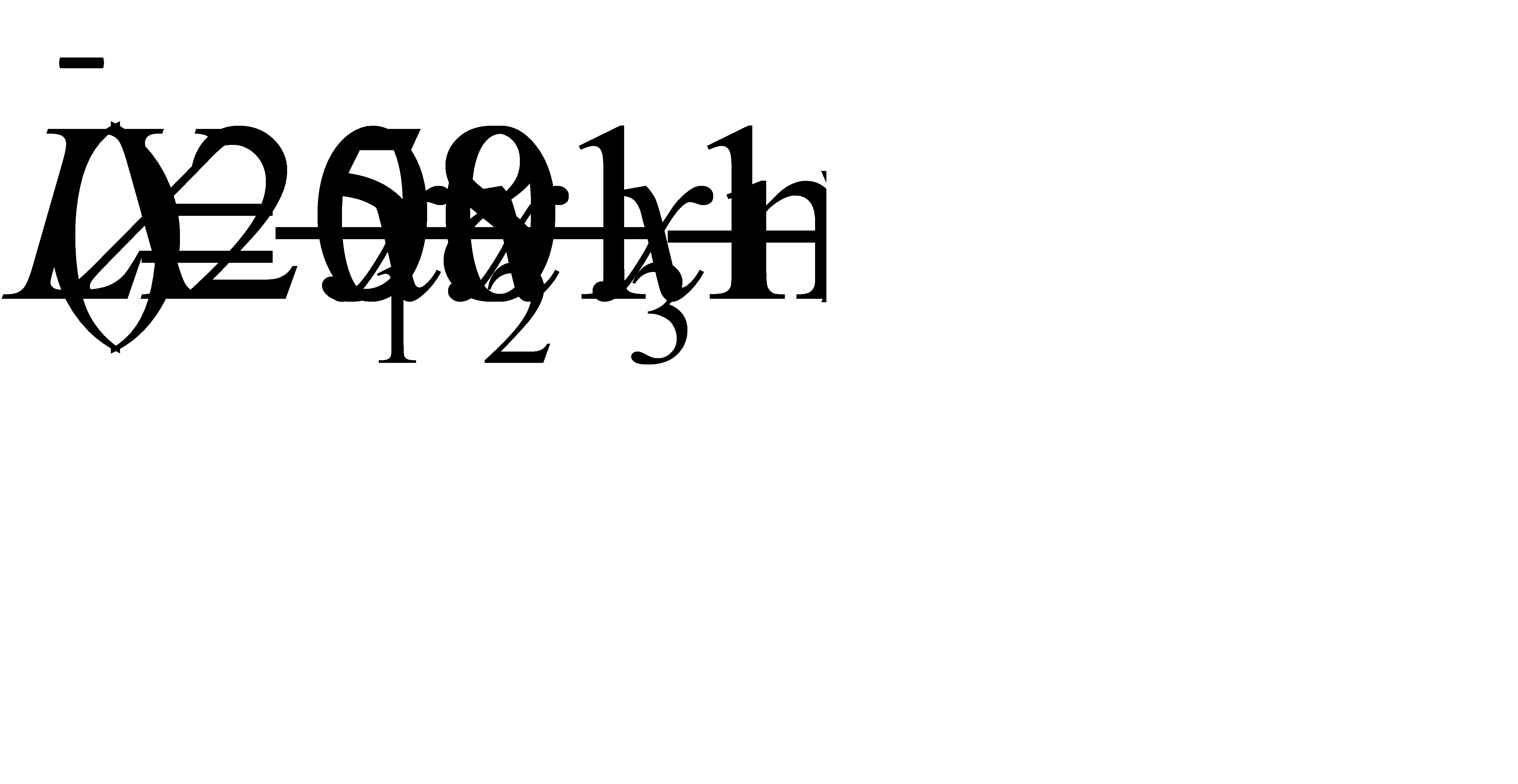. (4.3)

Систему ограничений (4.1) приведем к системе неравенств смысла «≤», умножив обе части I и II неравенств на (−1).

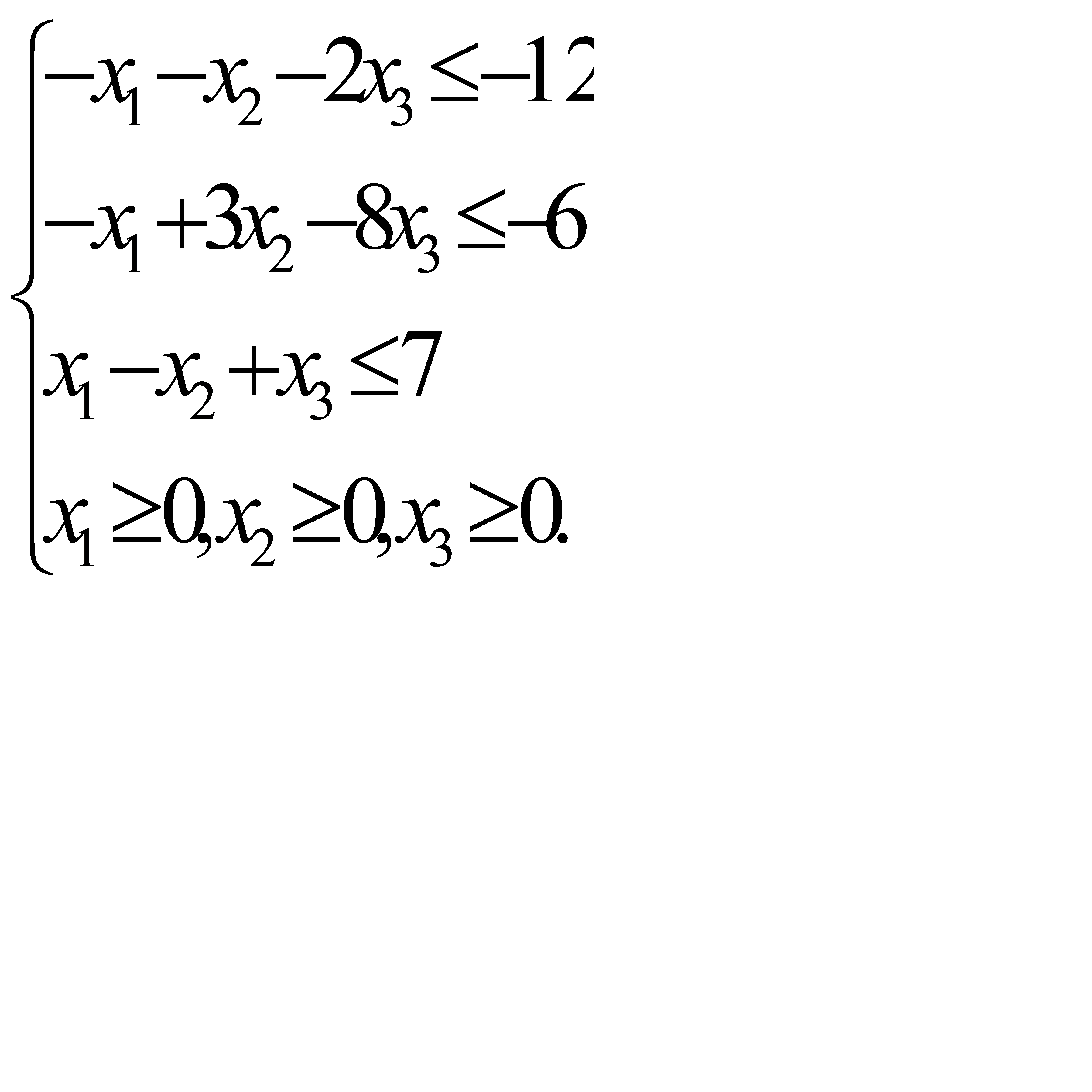
Перейдем к системе уравнений:

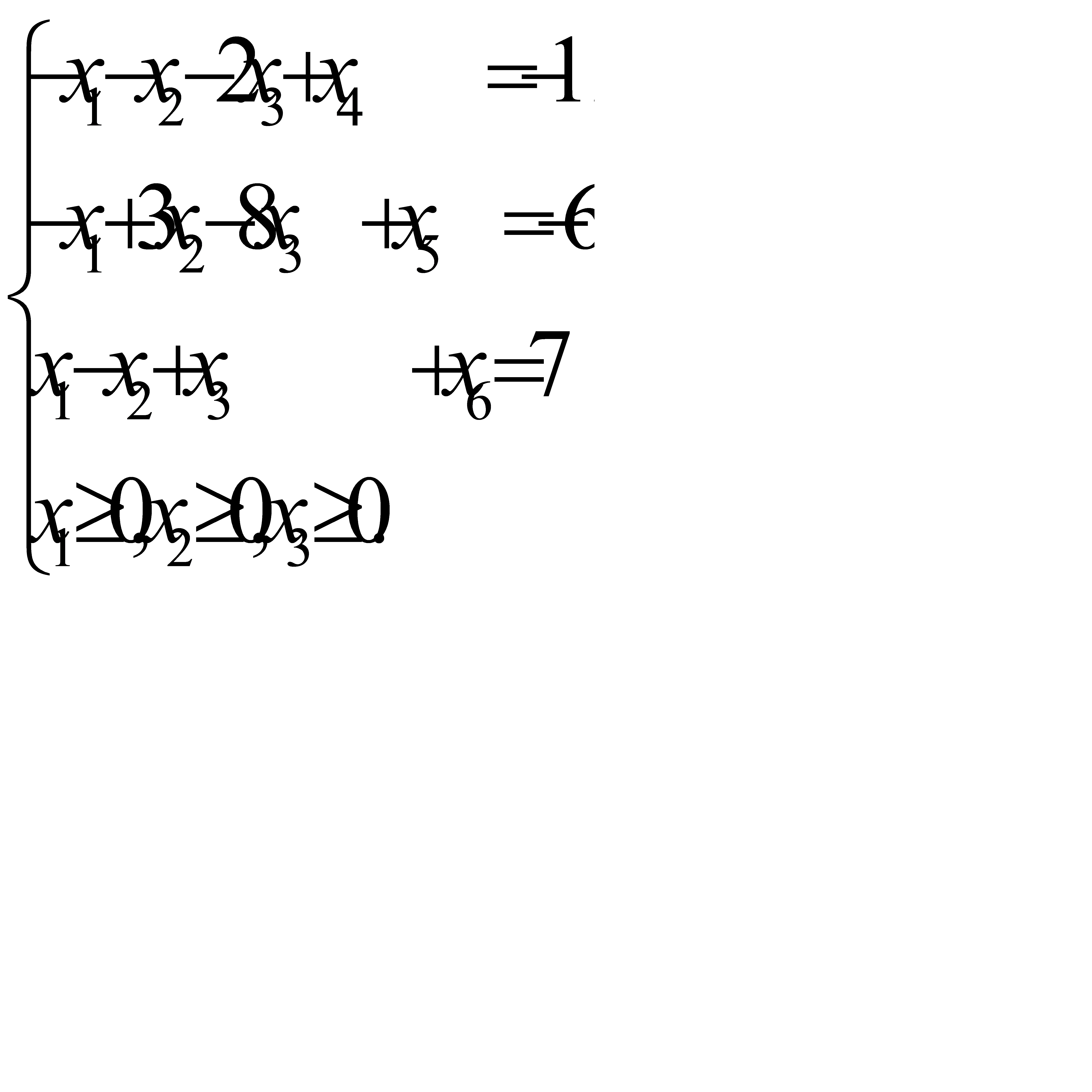(4.5)

За базис выбираем систему векторов - В системе уравнений А₄, А₅, А₆, так как эти векторы единичные и линейно независимые. Соответствующие единичным векторам переменные 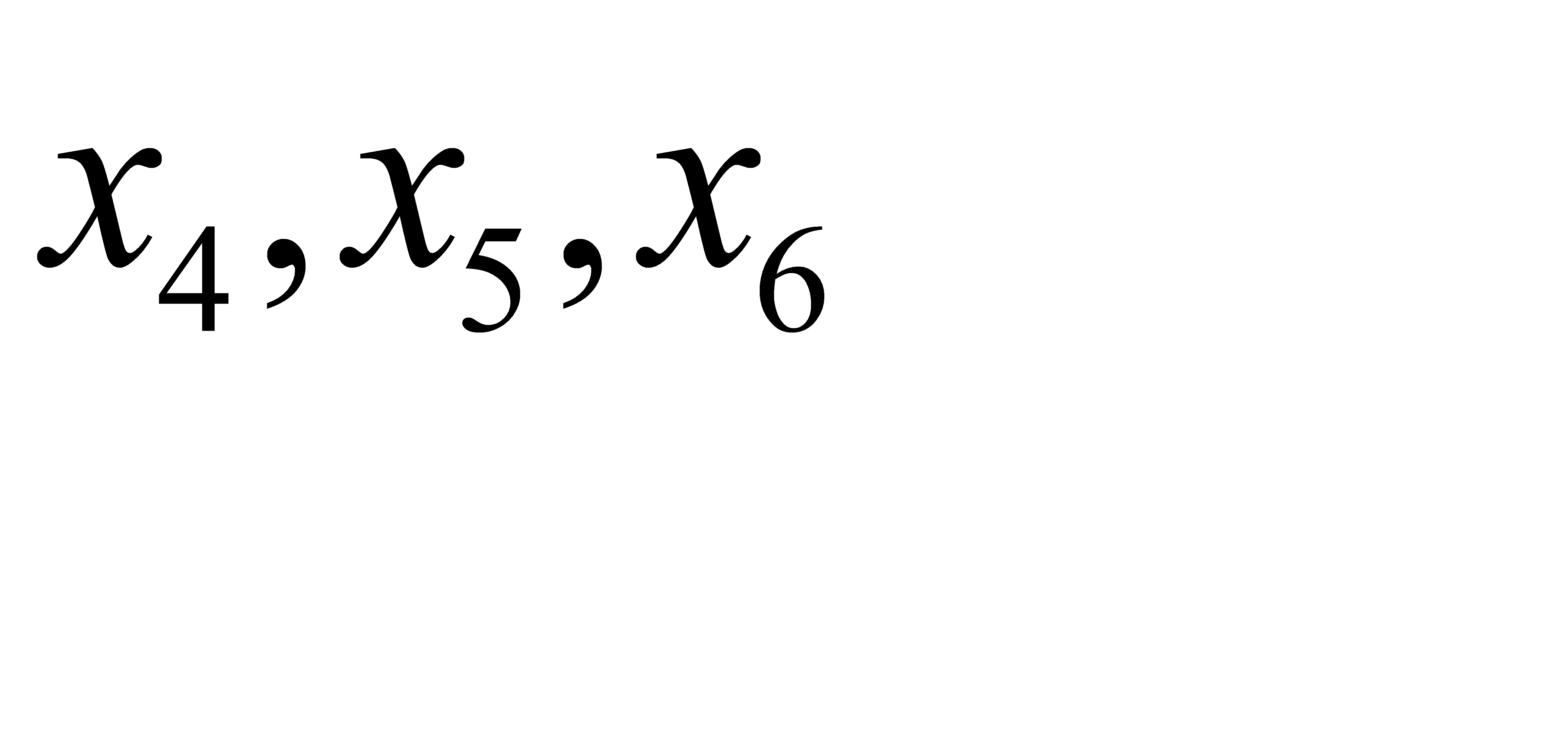являются базисными.

Разрешим систему уравнений (4.5) относительно базисных переменных

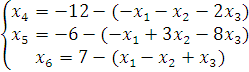(4.6)

Функцию цели запишем в виде:

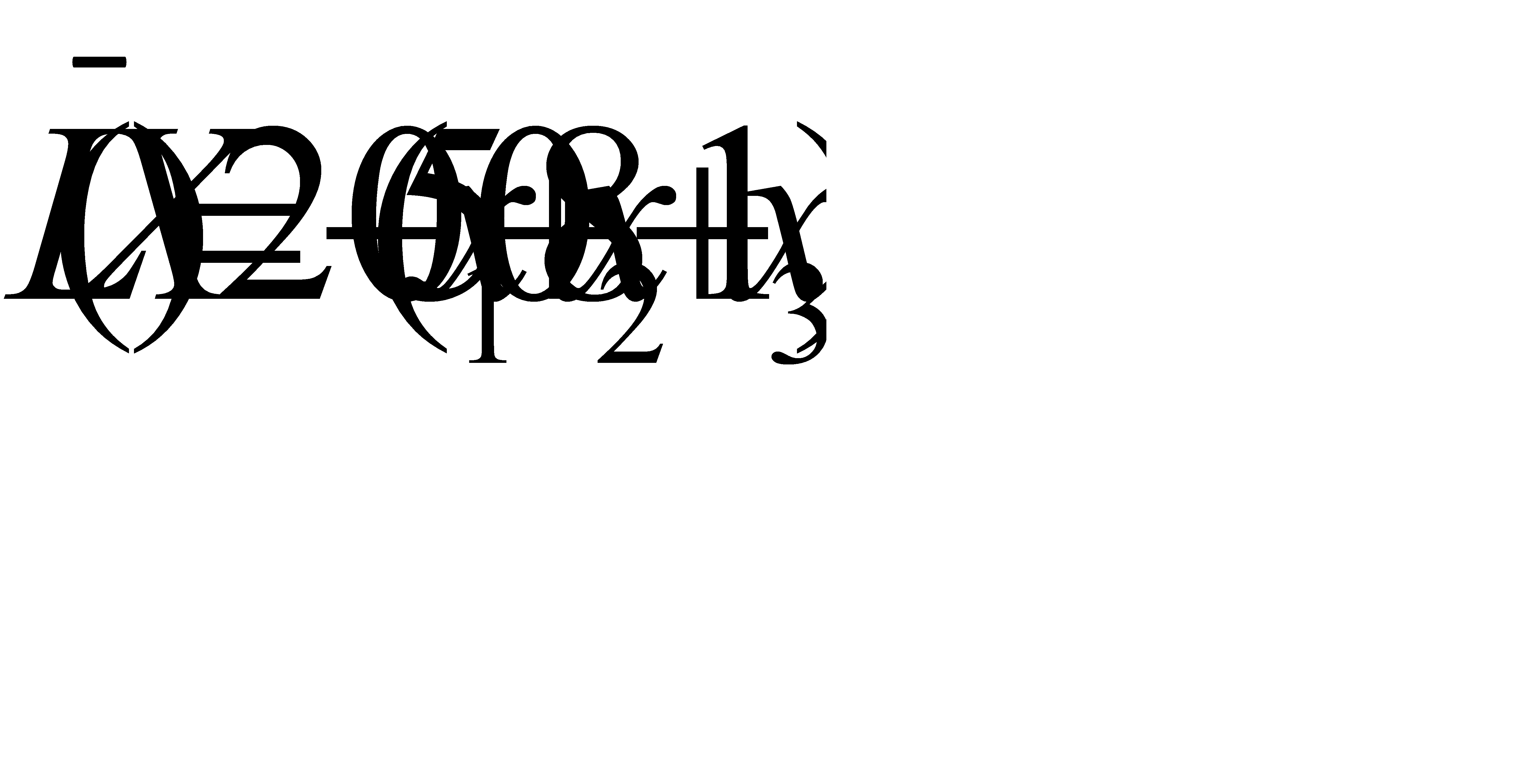. (4.7)

Полагая, что свободные переменные 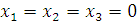, получим первый опорный план, который заносим в симплексную таблицу 1.

, .

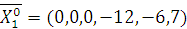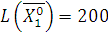В таблице 1 псевдоплан или условно-оптимальный план, так как условие оптимальности в индексной строке выполняется, а в столбце свободных членов имеются отрицательные значения. Следовательно, переходим к следующему этапу алгоритма – определению направляющих строки и столбца.

Среди отрицательных значений столбца свободных членов выбираем наибольший по абсолютной величине. Так как |−12| > |−6|, то первая строка, соответствующая переменной 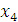, является направляющей, а переменную 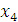нужно вывести из базиса.

Для выбора направляющего столбца коэффициенты индексной строки делим на соответствующие отрицательные коэффициенты направляющей строки: ; ; .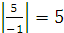

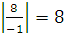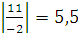Результаты деления, взятые по абсолютной величине, заносим в строку q. Из полученных qj выбираем min{5; 8; 5,5} = 5, которое соответствует первому столбцу с переменной x₁. Данный столбец является направляющим, а переменную x₁следует ввести в базис. На пересечении направляющих строки и столбца находится разрешающий элемент, равный (−1). Далее выполняем преобразование симплексной таблицы методом Жордана-Гаусса и заполняем таблицу 2.

Третий опорный план (таблица 3) является оптимальным, так как в индексной строке условие оптимальности выполняется и все значения базисных переменных – положительные числа:

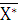= (2; 0; 5; 0; 36; 0), L( 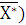= 135.

Таблица 1	Базисные переменные	Свободные члены (значения базисных переменных)	x₁	x₂	x₃	x₄	x₅	x₆
x₄	−12	-1	−1	−2
x₅	−6	−1		−8
x₆			−1

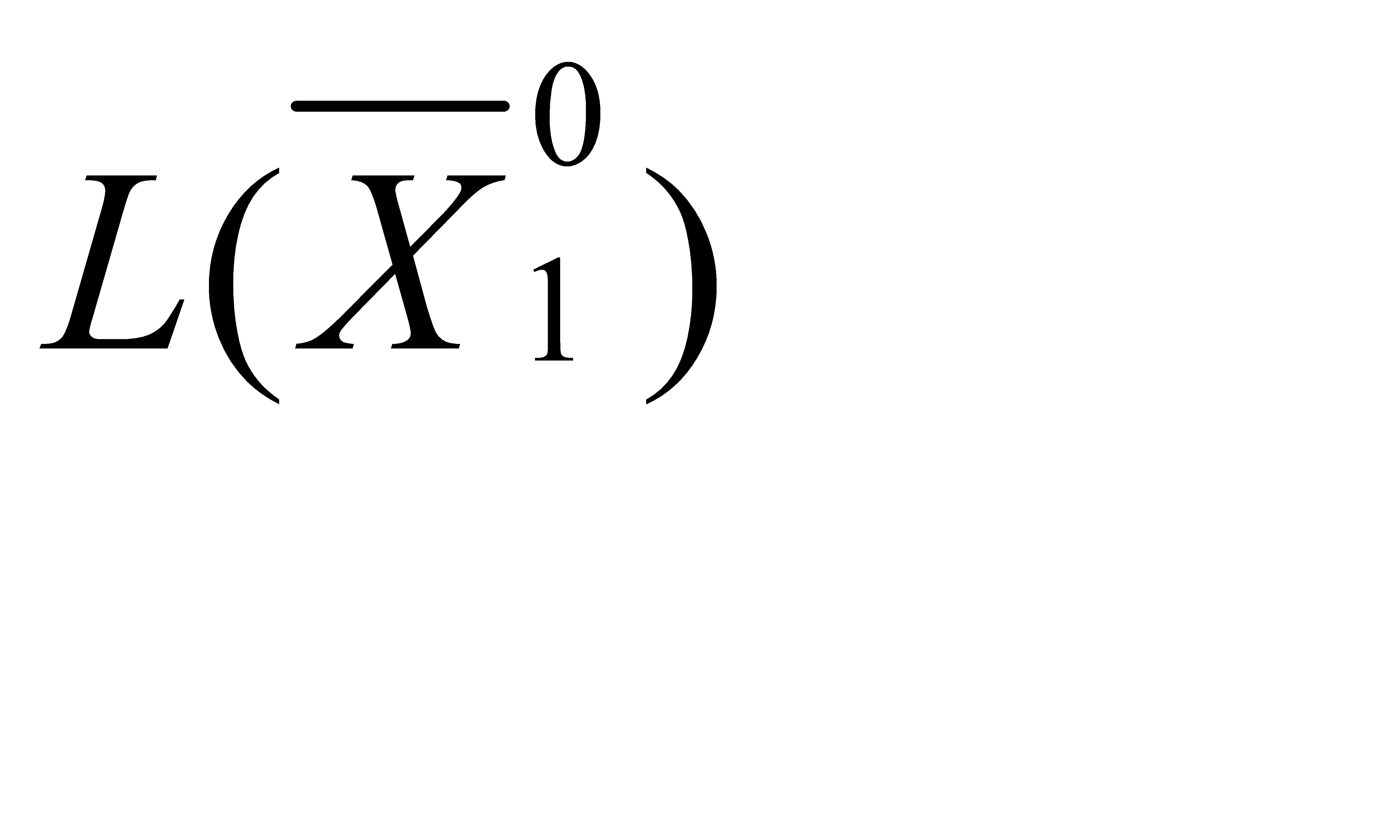
q				5,5	−	−	−
Таблица 2	x₁					−1
x₅				−6	−1
x₆	−5		−2	−1

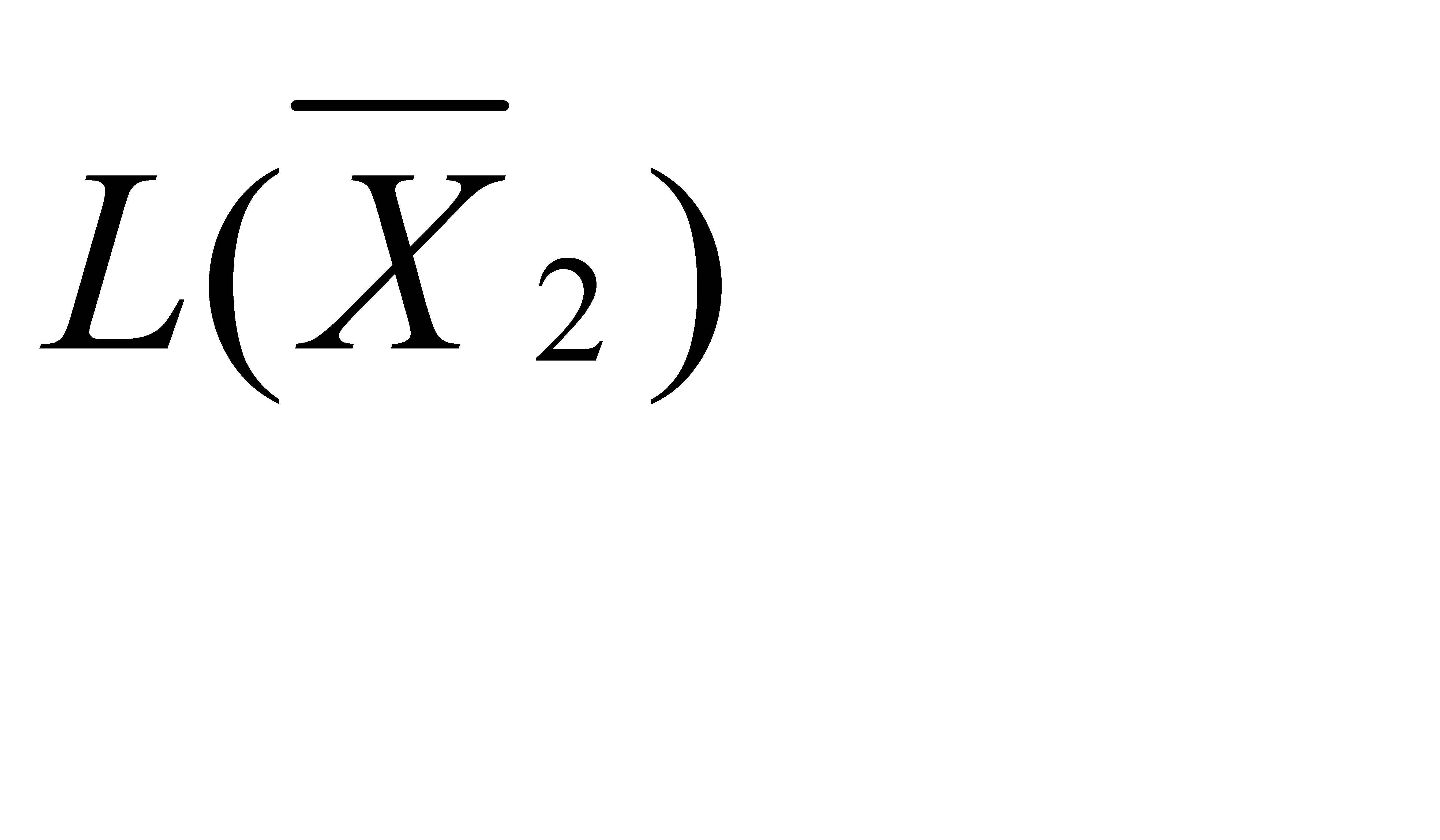
q		−	1,5		−	−	−
Таблица 3	x₁			−3				−2
x₅					−7		−6
x₃					−1		−1

1 234

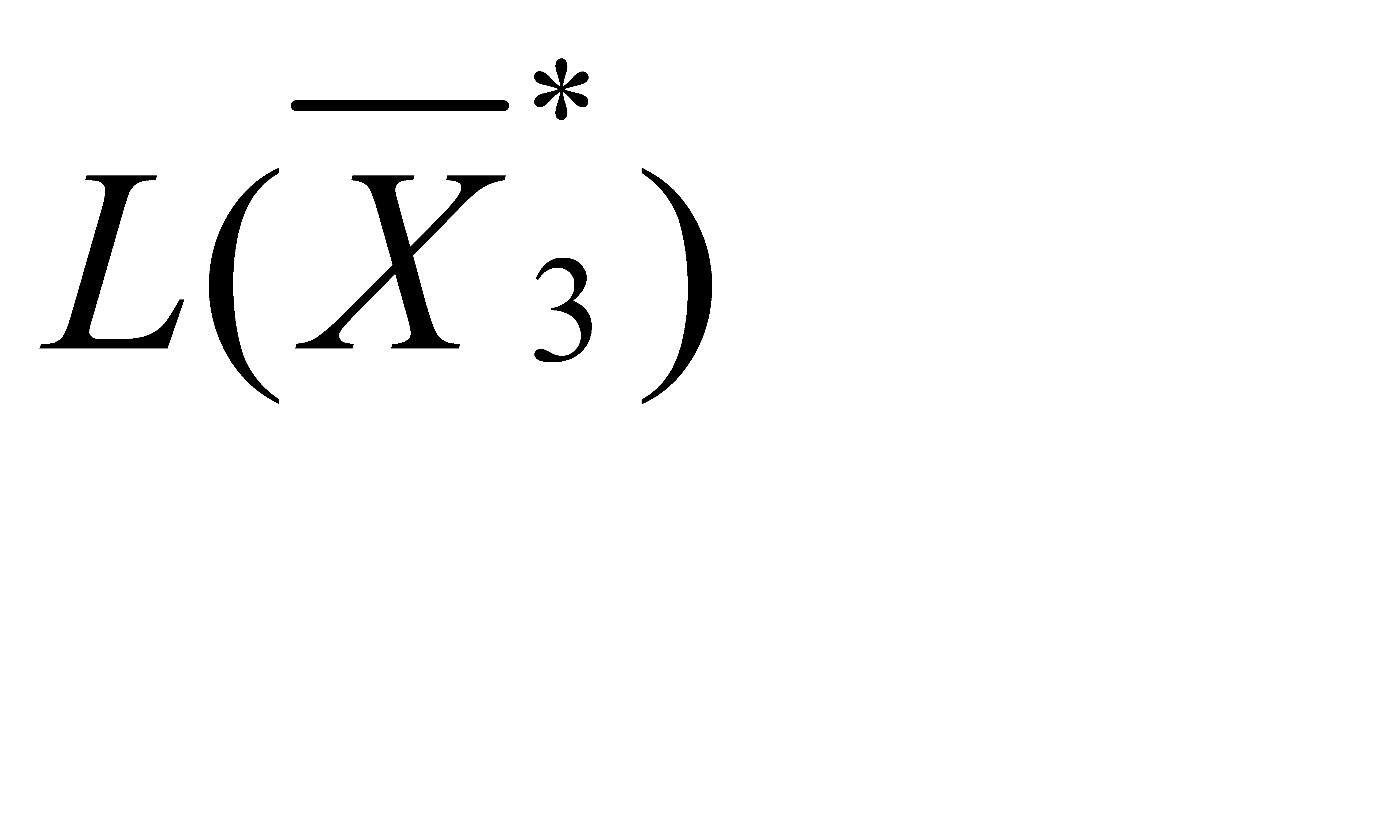
Дата добавления: 2017-05-18; просмотров: 657;