Вторая теорема двойственности

Пусть имеется симметричная пара двойственных задач

, ,

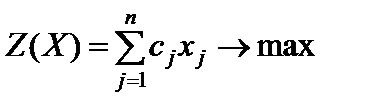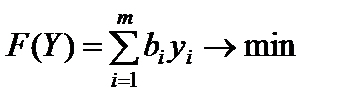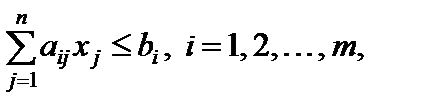
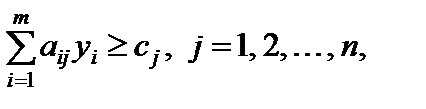(5.21)

. .

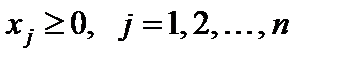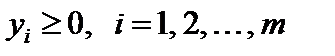Теорема 5.2. Для того чтобы допустимые решения 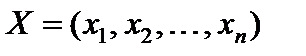, 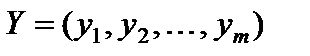являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства

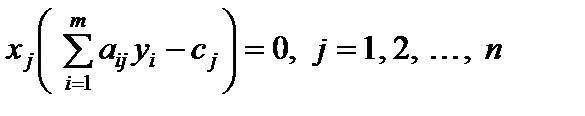; (5.22)

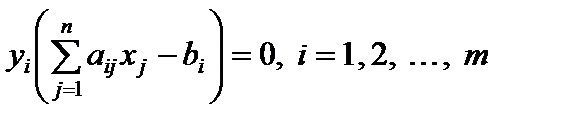. (5.23)

Иначе, если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи выполняется как строгое неравенство, то i-я координата оптимального решения двойственной задачи равна нулю и, наоборот, если i-я координата оптимального решения двойственной задачи отлична от нуля, то i-е ограничение исходной задачи удовлетворяется оптимальным решением как равенство.

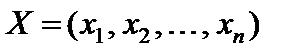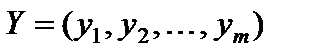Доказательство. Необходимость. Пусть и – оптимальные решения пары двойственных задач (5.21).

1. Покажем, что в этом случае выполняются равенства (5.22).

Подставим оптимальные решения X, Y в системы ограничений своих задач, получим

;

.

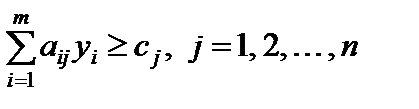Затем каждое из тождеств умножим на соответствующую переменную двойственной задачи и после этого просуммируем их, получим

.

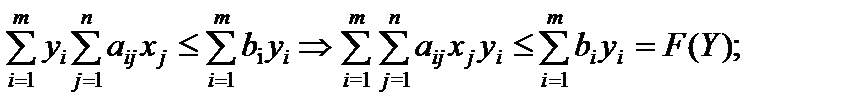
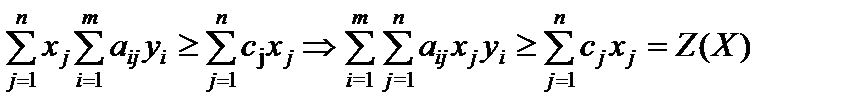Отсюда следует

.

Так как X, Y - оптимальные решения, то по первой теореме двойственности Z(X) = F(Y). Поэтому заменим в последнем соотношении знаки "£" на "=", получим

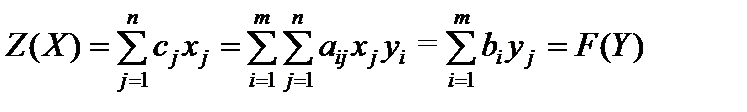. (5.24)

Отсюда можно записать

.

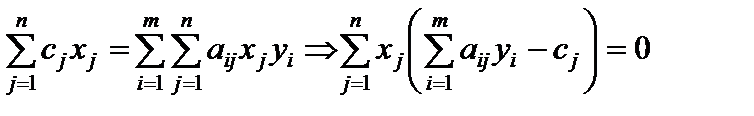Учитывая, что и 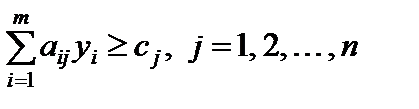, а следовательно и 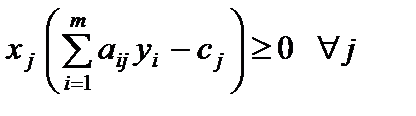, приходим к выводу, что каждое слагаемое суммы равно нулю, т. е. справедливы равенства (5.22)

.

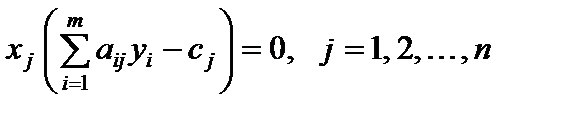2. Аналогично докажем справедливость равенств (5.23). Используя выражения (5.24), запишем

.

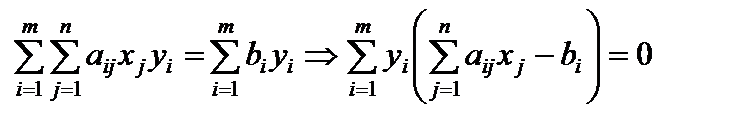Учитывая, что 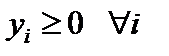и , делаем вывод, что каждое слагаемое суммы равно нулю, т. е.

.

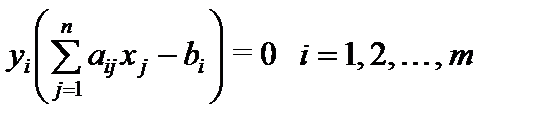Необходимость доказана.

Достаточность. Пусть равенства (5.22), (5.23) выполняются. Докажем, что в этом случае Х = (х₁,х₂,…,x_n) и Y = (y₁,y₂,…,y_n) являются оптимальными решениями.

Просуммируем каждую группу данных равенств, получим

;

.

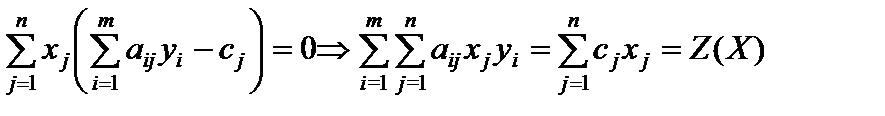Из данных равенств следует, что Z(X) = F(Y). Из первой теоремы двойственности (теорема 5.1) следует, что значения целевых функций пары двойственных задач равны только на оптимальных решениях. Поэтому можно утверждать, что X и Y являются оптимальными решениями. Теорема доказана полностью.

Пример 5.5. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности, найти решение исходной задачи.

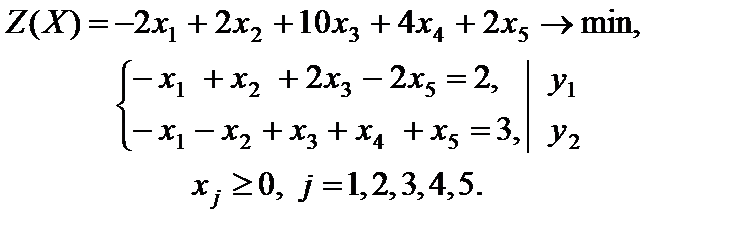
Решение. Составим двойственную задачу

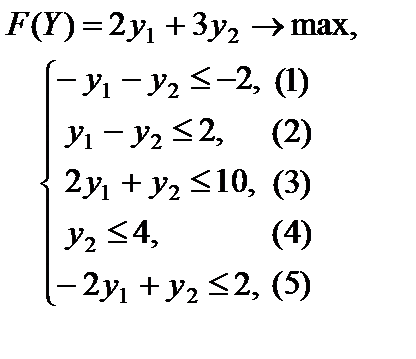
Решим эту задачу графическим методом. На рис. 5.1 изображены область допустимых решений задачи, нормаль 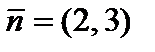линий уровня, линии уровня и оптимальное решение задачи .

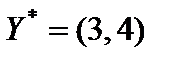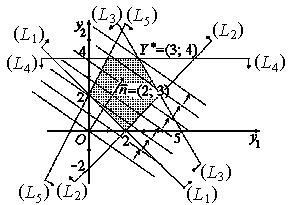
Рис. 5.1

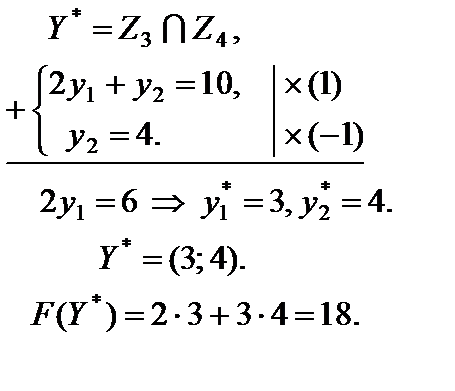
Подставим оптимальное решение 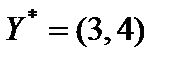в систему ограничений. Получим, что первое, второе и пятое ограничения выполняются как строгие неравенства.

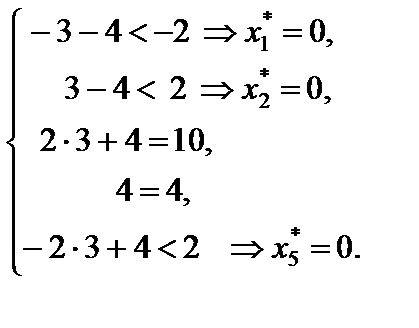
По второй теореме двойственности следует, что соответствующие координаты оптимального решения двойственной задачи, т. е. исходной задачи, равны нулю 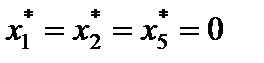. Учитывая это, из системы ограничений исходной задачи получим

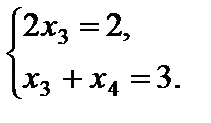
Отсюда находим 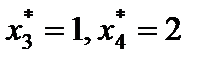. Окончательно записываем .

Ответ: min Z(X) = 18 при Х^* = (0, 0, 1, 2, 0).

Пример 5.6. Для данной задачи составить двойственную, решить ее графическим методом и, используя вторую теорему двойственности, найти решение исходной задачи.

Решение. Составляем двойственную задачу

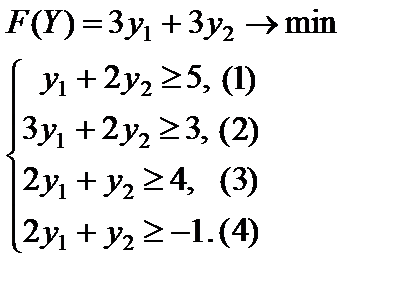
Решаем ее графическим методом (рис. 5.2). Для этого строим область допустимых решений (ОДР), нормаль 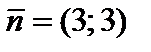линий уровня 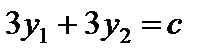и одну из линий уровня, которую перемещаем до опорной прямой. Оптимальное решение (точку 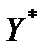) найдем, решая совместно уравнения прямых 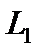и :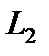

Имеем Y* = (1, 2), min F(Y*) = 9.

Þ Þ

Второе и четвертое ограничения выполняются как строгие неравенства, следовательно, вторая и четвертая координаты оптимального решения исходной задачи равны нулю , Учитывая это, первую и третью координаты оптимального решения найдем при совместном решении уравнений-ограничений исходной задачи

Ответ: max Z(X) = 9 при =(1, 0, 1, 0).

Лекция №9

Двойственный симплексный метод

Двойственный симплексный метод обязан своим возникновением теории двойственности, поэтому он и называется двойственным.

Двойственный симплексный метод, как и обычный симплексный метод, позволяет в результате последовательного улучшения так называемых почти допустимых опорных решений либо найти оптимальное решение, либо сделать заключение об отсутствии решения.

Алгоритм двойственного симплексного метода построен так, что, как только почти допустимое опорное решение становится допустимым, так оно становится и оптимальным. Порядок улучшения решений в симплексном и двойственном симплексном методах схематически изображен на рис. 5.2.

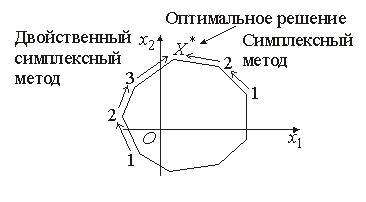
Рис. 5.2

В симплексном методе улучшаются опорные решения с неотрицательными координатами, а в двойственном симплексном методе улучшаются почти допустимые опорные решения с неположительными координатами.

Пусть имеется задача линейного программирования в канонической форме

,

,

.

Почти допустимым опорным решением (ПДОР) задачи линейного программирования называется такой n-мерный вектор 0, …, 0 ), который удовлетворяет системе ограничений задачи, не удовлетворяет условиям неотрицательности переменных и для которого векторы условий , соответствующие отличным от нуля координатам, являются линейно независимыми.

В двойственном симплексном методе рассматриваются ПДОР, при которых оценки разложений векторов условий по базису ПДОР соответствуют признаку оптимальности, т. е. в задаче на максимум , в задаче на минимум .

Для обоснования двойственного симплексного метода докажем три теоремы.

Теорема 5.3 ( признак оптимальности ПДОР). Почти допустимое опорное решение является оптимальным, если оно принадлежит области допустимых решений.

Доказательство. Пусть задача линейного программирования на максимум имеет начальное ПДОР, при котором оценки разложений векторов условий неотрицательные ( ). Алгоритм двойственного симплексного метода построен так, что при переборе ПДОР оценки поддерживаются неотрицательными. Поэтому, если от ПДОР переход будет к допустимому решению, то оно становится оптимальным, так как это соответствует признаку оптимальности обычного симплексного метода. Аналогично можно провести рассуждения с задачей на минимум.

Теорема 5.4 (об улучшении ПДОР). Если в задаче линейного программирования на максимум (минимум) для заданного почти допустимого опорного решения с неотрицательными (неположительными) оценками хотя бы одна координата отрицательная и при этом среди коэффициентов разложений векторов условий по базису данного решения существует хотя бы один отрицательный , то решение может быть улучшено (приближено к оптимальному), т. е. можно построить новое почти допустимое опорное решение, для которого значение целевой функции будет меньше (больше), если из его базиса вывести вектор , а ввести вектор , номер которого находится из условия

.

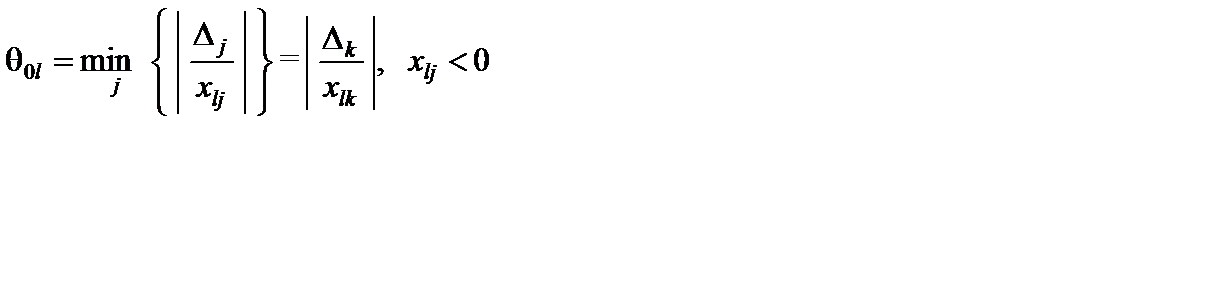Т а б л и ц а 5.4

Доказательство. Пусть задача линейного программирования на максимум имеет начальное ПДОР с базисом . Будем считать, что оценки разложений всех векторов условий по базису решения неотрицательные ( ) (табл. 5.4).

Получим сначала условие, обеспечивающее сохранение неотрицательности оценок при переходе к новому ПДОР, а затем условие для улучшения ПДОР (уменьшения значения целевой функции на этом решении).

1. Выведем формулы для пересчета оценок при проведении преобразования Жордана с разрешающим элементом . Формулы пересчета коэффициентов разложения векторов условий по базису опорного решения имеют вид

,

.

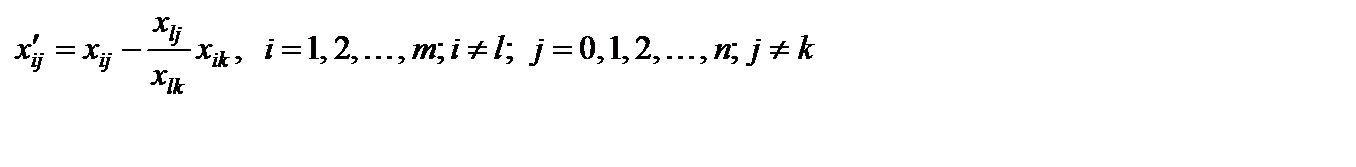Оценки для первого ПДОР находятся по формуле

.

После вывода из базиса вектора и введения в базис вектора 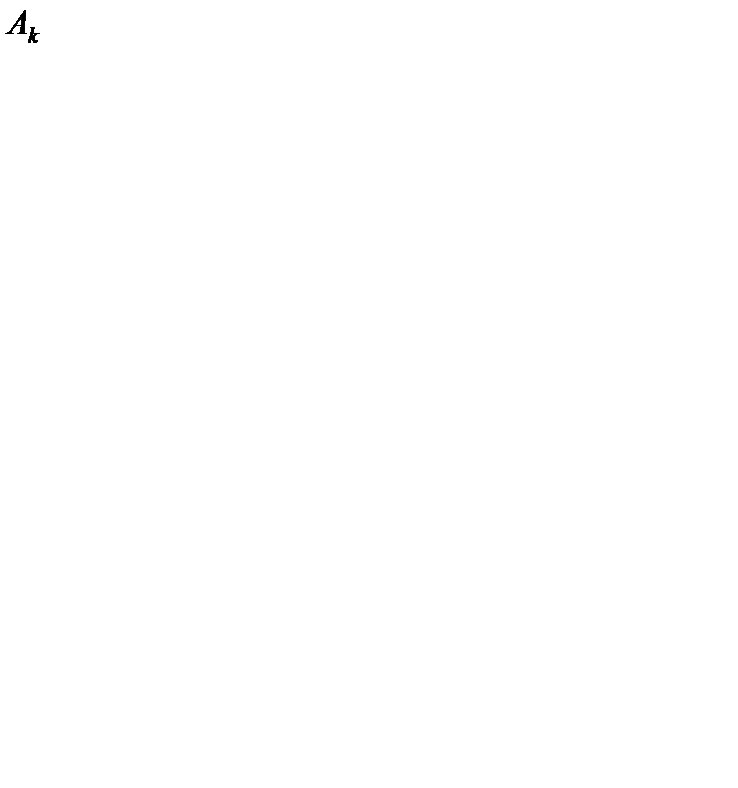(разрешающий элемент преобразования Жордана ) оценки при следующем ПДОР будут равны

.

Подставив в это выражение, получим

.

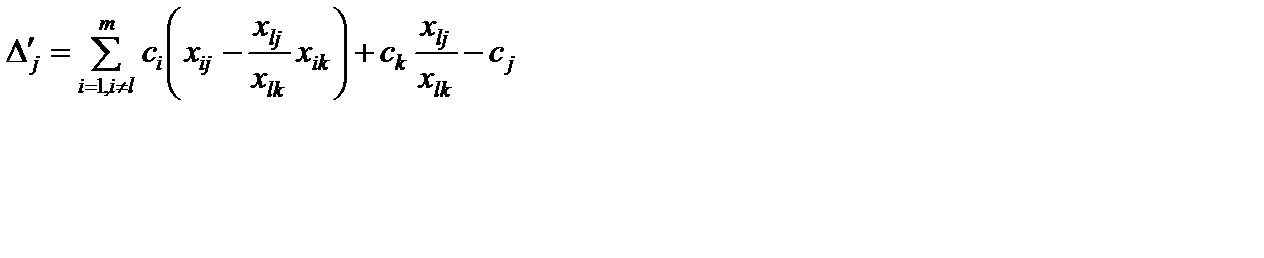Преобразуем данное выражение

.

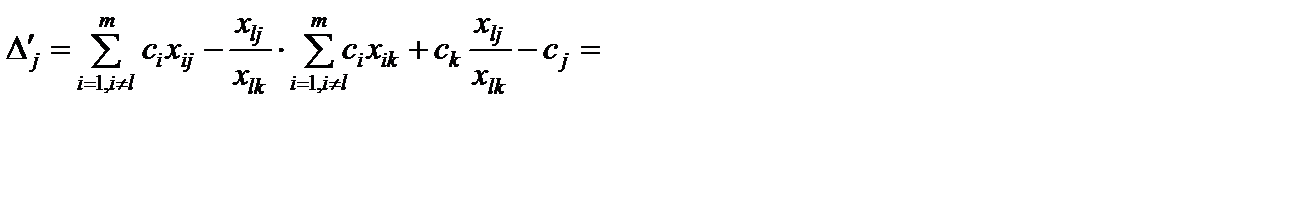
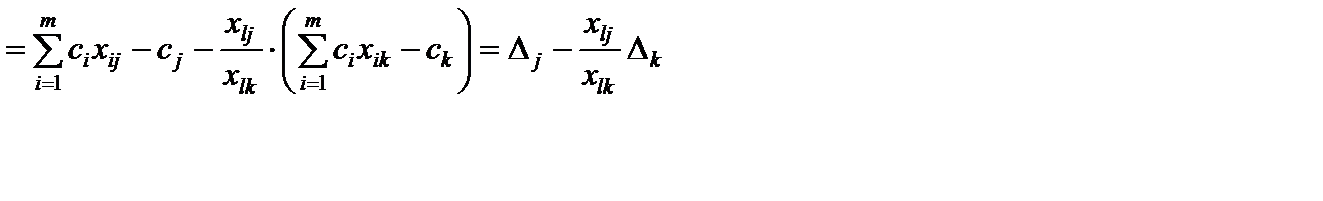Имеем следующую формулу для пересчета оценок

, . (5.25)

Пусть . Теперь необходимо получить ограничения на выбор разрешающего элемента , обеспечивающего неотрицательность оценок .

Первое условие следует из неотрицательности оценки для вектора , выводимого из базиса (его оценка была равна нулю ). Так как 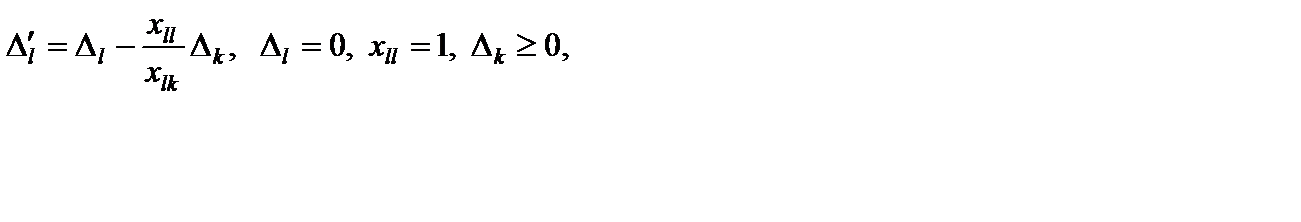то при

Следовательно, разрешающий элемент должен быть отрицательным

. (5.26)

Оценки для всех остальных векторов должны оставаться неотрицательными. Рассматриваем два случая:

а) если , то без дополнительных условий, так как , ;

б) если , то записав неравенства ,
j =1, 2, ..., n в виде , j = 1, 2, ..., n и умножив на , имеем , j = 1, 2, ..., n.

С учетом того, что , так как , получим

, j = 1, 2, ..., n..

Следовательно, для того чтобы оценки , j = 1, 2, ..., n были неотрицательными, номер вектора , вводимого в базис, должен выбираться из условия

, . (5.27)

Данное условие в задачах на минимум также позволяет сохранять оценки , j = 1, 2, ..., n неположительными.

2. Далее получим условие выбора номера l вектора , выводимого из базиса. При обосновании симплексного метода (теорема 4.1 об улучшении опорного решения) была получена формула для приращения целевой функции при переходе от одного опорного решения к другому (при введении в базис опорного решения вектора )

.

Преобразуем ее

.

Учитывая, что , , получим . Обозначим . Тогда формула для вычисления приращения целевой функции в случае выведения из базиса почти опорного решения вектора будет иметь вид

. (5.28)

Чтобы в задаче на максимум значение целевой функции убывало, приращение должно быть отрицательным. Это можно обеспечить только выбором отрицательной координаты ПДОР.

Для наибольшего приближения к оптимальному решению номер выводимого из базиса вектора должен выбираться из условия

. (5.29)

В задачи на минимум это условие имеет вид

. (5.30)

Теорема 5.5 (об отсутствии решения задачи ввиду несовместности системы ограничений). Если для ПДОР существует хотя бы одна отрицательная координата и при этом не существует отрицательного коэффициента разложений векторов условий ,
j = 1, 2, ..., n, то задача не имеет решения ввиду несовместности системы ограничений.

Доказательство. Пусть в результате эквивалентных преобразований системы уравнений ограничений задачи некоторое уравнение приняло вид

,

где .

Ввиду того, что оптимальное решение задачи является допустимым, его координаты должны быть неотрицательными и оно не может удовлетворять данному уравнению, так как левая и правая части уравнения принимают значения разных знаков.