Задача коммивояжера
Имеются n пунктов или городов с заданными расстояниями 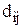 между i-м и j-м пунктами. Необходимо составить оптимальный маршрут из условия минимизации суммарного расстояния для коммивояжера, выходящего из пункта с номером 1, который должен побывать во всех пунктах ровно по одному разу и вернуться в исходный пункт.
между i-м и j-м пунктами. Необходимо составить оптимальный маршрут из условия минимизации суммарного расстояния для коммивояжера, выходящего из пункта с номером 1, который должен побывать во всех пунктах ровно по одному разу и вернуться в исходный пункт.
Введем альтернативные бинарные переменные :
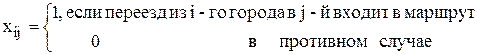 .
.
Условия минимизации общего расстояния , а также прибытия в каждый пункт и выезда из него ровно по одному разу могут быть выражены следующим образом:
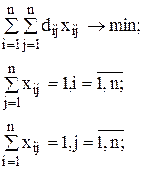
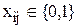 .
.
Однако необходимо обеспечить непрерывность маршрута, чтобы набор звеньев, входящих в маршрут, образовывал единую цепочку (например, при n=8 цепочка (1,2) - (2,6) - (6,4) - (4,8) - (8,5) - (5,3) - (3,7) - (7,1)), а не состоял бы из отдельных не связанных цепочек (например, (1,2) - (2,6) - (6,1) и (3,8) - (8,7) - (7,5) - (5,4) - (4,3)). Для устранения замкнутых циклов (подобходов), включающих количество вершин меньшее n, в модель вводятся n дополнительные переменных ui³0 ( 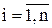 ) и n2 дополнительных ограничений:
) и n2 дополнительных ограничений:
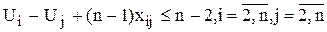 .
.
Действительно, пусть маршрут включает несколько цепочек. Тогда существует цепочка, начинающаяся и заканчивающаяся в начальном пункте, но включающая n1 звеньев, где n1<n. Просуммировав эти неравенства вдоль такой цепочки (т.е. при xik=1), получим бессмысленное неравенство n1(n-1)£n1(n-2) (все ui и uj при суммировании взаимно уничтожаются). Покажем теперь, что для маршрута, исключающего подобходы, это неравенство выполняется, т.е., можно найти значения ui, удовлетворяющие дополнительным ограничениям. Положим ui=p, если город i посещается коммивояжером на p-м шаге, p= 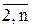 . Отсюда следует, что
. Отсюда следует, что 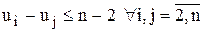 . Таким образом, ограничения выполняются для всех
. Таким образом, ограничения выполняются для всех 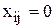 . При
. При 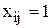 эти ограничения превращаются в равенства
эти ограничения превращаются в равенства
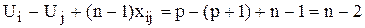 .
.
Задача коммивояжера имеет широкий круг практических приложений. К ней сводятся задачи оптимальной маршрутизации (выбор маршрутов перевозки грузов, маршрутов движения транспорта, минимизация расстояния, проходимого исполнительным механизмом станка с ЧПУ и т.д.), задачи проектирования электрических и вычислительных сетей, задачи определения последовательности обработки деталей на станках с условием минимизации времени переналадок и т.д.
Пример 11. Пусть необходимо проложить коммуникации между n различными ЭВМ таким образом, чтобы каждая ЭВМ была связана с двумя соседними, вся сеть была бы подключена к центральной ЭВМ, а суммарная длина коммуникаций была бы минимальна. . Заданы расстояния dij между i-й и j-й ЭВМ.
Данная задача формализуется в виде задачи коммивояжера следующим образом:
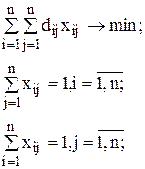
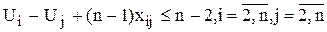 ;
;
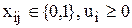 .
.
При этом xij=1, если i-я и j-я ЭВМ соединяются.
Задача о покрытии
Пусть имеется n предметов, каждый из которых обладает некоторым числом признаков из заданного множества m признаков, а в совокупности эти n предметов обладают всеми m признаками. Необходимо выбрать минимальное число предметов, которые в совокупности обладали бы m признаками. Условия задачи задаются матрицей A с элементами
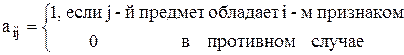
Введем бинарные переменные:
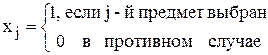 .
.
Тогда математическая модель задачи имеет следующий вид:
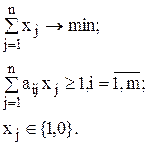
Каждое i-е ограничение в данном случае показывает, что должен быть выбран хотя бы один предмет, обладающий i-м признаком.
Если каждому j-му предмету приписывается вес 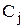 , может быть сформулирована взвешенная задача о покрытии:
, может быть сформулирована взвешенная задача о покрытии:
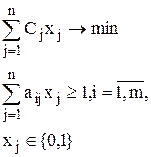
Если каждому i-му признаку приписывается натуральное число 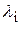 и требуется найти минимальное число таких предметов, что i-м признаком обладает не менее
и требуется найти минимальное число таких предметов, что i-м признаком обладает не менее 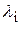 предметов из указанного набора, получаем задачу о кратном покрытии:
предметов из указанного набора, получаем задачу о кратном покрытии:
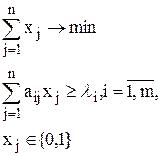
Задача о разбиении. Задача о разбиении аналогична задачи о покрытии с тем отличием, что признаки у различных предметов не должны совпадать:
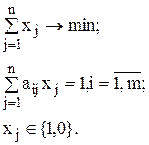
Задача о взвешенном разбиении формулируется следующим образом:
К задаче о покрытии сводится широкий круг задач информационного поиска, синтеза логических схем, задачи разбиения электронных схем на модули и покрытия схем типовыми ячейками и т.д.
Пример. Пусть некоторое количество информации хранится в n массивах (файлах) длины 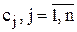 , причем на каждую единицу информации отводится по крайней мере один массив. Задана матрица T с элементами
, причем на каждую единицу информации отводится по крайней мере один массив. Задана матрица T с элементами
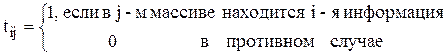
Получена заявка на m типов единиц информации. Необходимо определить подмножество массивов минимальной длины, необходимых для удовлетворения заявки.
Введем бинарные переменные:
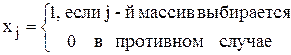 .
.
Тогда математическая модель задачи формализуется в виде задачи о покрытии:
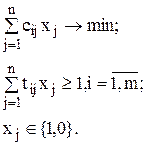
Методы решения задач дискретной оптимизации.
Методы решения задач дискретной оптимизации делятся на следующие группы:
1. Методы отсечения
2. Комбинаторные
3. Приближенные
Методы отсечения используются только для решения линейных задач, а комбинаторные и приближенные методы - для всех (и линейных и нелинейных задач).
Методы отсечения
Рассмотрим целочисленную ЗЛП.
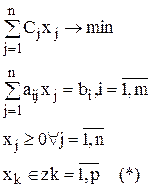
Если p=n, то это задача полностью целочисленная, если нет - то частично целочисленная. Обозначим ЗЦЛП через z, область допустимых решений Dz, оптимальное решение задачи Xz*.
Обозначим соответственно ЗЛП без условия (*) через P, область дополнительных решений - D, оптимальное решение - X*. Предположим, что область D - выпуклое ограниченное множество. Тогда Dz представляет собой дискретное множество точек с целочисленными координатами, которые принадлежат D, то есть 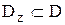 .
.
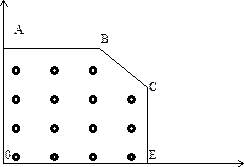
ЗЦЛП z и ЗЛП Р характеризуются следующими свойствами:
1) Минимальное значение целевой функции в z всегда больше минимального значения этой же целевой функции в p.
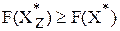 . Таким образом, значение целевой функции в точке непрерывного оптимума является нижней границей значения целевой функции в точке дискретного оптимума.
. Таким образом, значение целевой функции в точке непрерывного оптимума является нижней границей значения целевой функции в точке дискретного оптимума.
2) Если 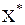 оказывается целочисленным, то оно является оптимальным решением задачи Z,
оказывается целочисленным, то оно является оптимальным решением задачи Z,
3) Если не имеет решений Р, то не имеет решений и Z.
Основная идея метода отсечения:
1. Решается последовательность задач ЛП 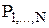 .
.
2. Каждая последующая задача ЛП получается из предыдущей путем добавления к ее условиям дополнительного линейного ограничения, называемого правильным отсечением. При этом l-тым отсечением называется дополнительное линейное ограничение, вводимое в задачу 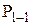 для образования задачи
для образования задачи 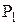 и характеризующаяся следующими свойствами:
и характеризующаяся следующими свойствами:
1) Каждое целочисленное решение задачи Z из области Dz ему удовлетворяет.
2) Нецелочисленное решение задачи Pl-1 ему не удовлетворяет (отсекается).
Таким образом в задаче P последовательно добавляются дополнительные ограничения (отсечения), не исключающее целочисленных допустимых точек и отсекающие нецелочисленные решения ЗЛП.
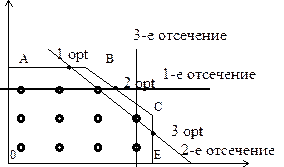
Отличие методов отсечения от других заключается в способах формирования дополнительных ограничений.
Алгоритм Гомори для решения полностью целочисленной ЗЛП.
Целой частью 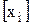 числа
числа 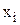 будем называть наибольшее целое число, не превосходящее
будем называть наибольшее целое число, не превосходящее 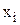 .
.
Дробная часть 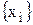 числа
числа 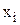 называется разность между числом
называется разность между числом 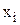 и его целой частью.
и его целой частью. 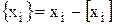
Пример.
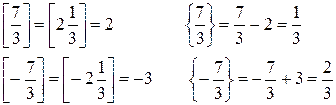
Основные шаги алгоритма.
1. Определение оптимальности решения ЗЛП без учета условий целочисленности симплекс-методом.
2. Если полученное решение ЗЛП является целочисленным, то останов, иначе 3.
3. В нецелочисленном оптимальном решении ЗЛП выбирается базисная переменная xk с наибольшей дробной частью.
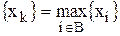 ,где
,где 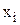 -базисные переменные; В- множество индексов базисных переменных.
-базисные переменные; В- множество индексов базисных переменных.
4. Для выбранной переменной 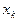 составляется дополнительное ограничение.
составляется дополнительное ограничение. 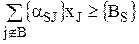 .
.
S - номер строки окончательной симплекс-таблицы, которой соответствует переменная xk.
5. Определение решения ЗЛП, получающейся из предыдущей в результате присоединения дополнительного ограничения. При этом дополнительное ограничение добавляется к последней симплекс-таблице. Для этого дополнительное ограничение преобразуется в уравнение :
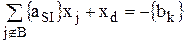
Затем полученное уравнение умножается на (-1). После добавляются ограничения к последней симплекс-таблице. ЗЛП решается двойственным симплекс-методом.
6. Переход к S2.
Пример.
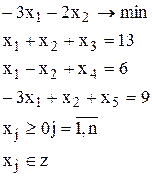
Пусть в результате решения симплекс-методом окончательная симплекс-таблица имеет вид:
| хб | Сб | b | -3 | -2 | ||||
| x1 | x2 | x3 | x4 | x5 | x6 | |||
| x2 | -2 | 7/2 | 1/2 | -1/2 | ||||
| x1 | -3 | 19/2 | 1/2 | 1/2 | ||||
| x5 | ||||||||
| -71/2 | -5/2 | -1/2 |
Составим дополнительное ограничение:
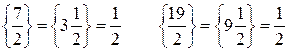
Дробные части равны между собой. Поэтому дополнительное ограничение составляется для любой переменной (обычно для первой). Составим ограничение для переменной 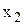 :
:
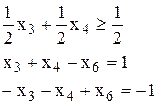
Добавляем это ограничение симплекс-таблице:
| x6 | -1 | -1 | -1 | |||||
| x2 | -1/2 | |||||||
| x1 | ½ | |||||||
| x5 | -1 | |||||||
| x4 | -1 | |||||||
| -35 | -2 | ½ |
После добавления дополнительного ограничения решается двойственным симплексным методом.
Оптимальный план (9; 4; 0; 1; 32).
ЗЦЛП не имеет решений в следующих случаях:
1) Если не имеет решений ЗЛП, то не имеет решений и ЗЦЛП
2) Если для дробного bS все asj окажутся целыми.
Метод Гомори для решения частично-целочисленных задач линейного программирования.
Алгоритм аналогичен предыдущему:
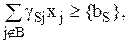
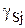 определяется из следующих соображений:
определяется из следующих соображений:
1) Для переменных 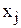 , которые могут принимать только целочисленные значения:
, которые могут принимать только целочисленные значения:
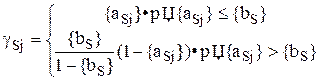
2) Для переменных 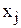 , которые могут принимать целочисленные значения:
, которые могут принимать целочисленные значения:
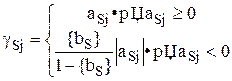
Достоинства метода.
Простота построения .Простая логика.
Возможность использовать стандартного ПО (для двойственного симплекс метода)
Недостатки.
Ограниченность применения – для решения только линейных целочисленных задач.
Низкая сходимость алгоритма.
Основная проблема метода Гомори – увеличение размерности задачи при добавлении дополнительных ограничений.
Комбинаторные методы решения задач дискретной оптимизации.
К комбинаторным методам решения ЗДО относятся методы, реализующие разложение схемы перебора допустимых вариантов. Наиболее распространенными и эффективными комбинаторными методами являются методы ветвей и границ.
Методы ветвей и границ.
МВиГ основаны на использовании конечности множества допустимых вариантов и замене полного перебора сокращенным направленным перебором. При этом полного перебора удается избежать за счет отбрасывания неперспективных множеств вариантов, т.е. тех множеств, где заведомо нет оптимального решения. В МВиГ все множество допустимых вариантов последовательно дробится на все меньшие подмножества. При этом вычисляются оценки (границы), которые позволяют сделать вывод о том, какое из полученных подмножеств может быть отброшено при условии сохранения подмножества, содержащего оптимальное решение. Для иллюстрации работы МВГ используется дерево, называемое деревом перебора (вариантов).
Обобщенный алгоритм МвиГ.
1) Для задачи вида 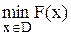 задачи вида
задачи вида 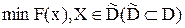 будем называть подзадачами.
будем называть подзадачами.
2) Релаксации задачи (или подзадачи) - это переход к задаче с той же целевой функцией, но с некоторой дополнительной областью D/, включающей D в качестве подмножества 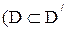 ).
).
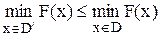
Оптимальное решение релаксации является нижней границей оптимального решения исходной задачи.
3) Ветвление - разбиение допустимой области на непересекающиеся подмножества и получение таким образом новых экстремальных подзадач. При этом подзадачи являются вершинами дерева вариантов.
4) Нижняя оценка (граница) 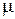 оптимального значения целевой функции в вершине i - это оптимальное решение задачи, полученной в результате релаксации подзадачи, соответствующей вершине i.
оптимального значения целевой функции в вершине i - это оптимальное решение задачи, полученной в результате релаксации подзадачи, соответствующей вершине i.
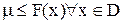 .
.
5) Верхняя оценка (граница) 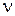 оптимальности решения - это значение целевой функции, обеспечиваемое некоторым дополнительным решением подзадачи i (для ЗЦП это целочисленное дополнительное решение).
оптимальности решения - это значение целевой функции, обеспечиваемое некоторым дополнительным решением подзадачи i (для ЗЦП это целочисленное дополнительное решение).
6) Рекорд - это min-ная верхняя оценка в вершинах дерева вариантов.
7) Прозондированные вершины - вершины, в которых дальнейшее ветвление невозможно и нецелесообразно.
Рассмотрим частично целочисленную задачу следующего вида:
Максимизировать Z = СX
при ограничениях AX = B, 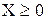 ,
,
хj - целочисленная переменная при jÎI,
где I - множество индексов целочисленных переменных задачи. Задача записана в векторной форме: С=(с1…сn) - вектор-строка коэффициентов целевой функции; X= 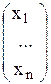 - вектор столбец переменных задачи; В=
- вектор столбец переменных задачи; В=  - вектор-столбец правых частей; A=
- вектор-столбец правых частей; A= 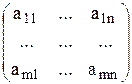 - матрица коэффициентов при переменных в системе ограничений.
- матрица коэффициентов при переменных в системе ограничений.
В качестве первого шага необходимо решить сформулированную задачу ЛП, рассматривая все ее переменные как непрерывные. Получаемая таким образом задача ЛП обозначается через ЛП-1, оптимальное значение ее целевой функции - через Z1. Пусть в оптимальном решении задачи ЛП-1 некоторые целочисленные переменные принимают дробные значения; тогда оптимальное решение исходной задачи не совпадает с оптимальным решением ЛП-1. В этом случае величина Z1 представляет собой верхнюю границу оптимального значения Z исходной задачи.
На следующем шаге проводится ветвление по одной из целочисленных переменных, имеющих дробное значение в оптимальном решении задачи ЛП-1. Для определения переменной, по которой производится ветвление, разработан ряд правил. Приведем некоторые из них.
1. Выбор целочисленной переменной с наибольшей дробной частью.
2. Приписывание целочисленным переменным приоритетов и ветвление по переменной с наибольшим приоритетом. Важность целочисленной переменной может определяться следующими соображениями:
- данная переменная является наиболее важной, ее значение ирает важную роль в модели по мнению разработчиков.
- коэффициент целевой функции при данной переменной превосходит остальные;
3. Находится то дополнительное ограничение, которое приводит к наибольшему возрастанию нижней границы. Цель - найти ту вершину, которая наиболее верно будет отброшена.
4. Произвольные правила выбора. Например, можно выбирать переменную с наименьшим номером.
Пусть ветвление происходит по целочисленной переменной хj, дробное значение которой в оптимальном решении ЛП-1, равно bj . Далее рассматриваются две новые задачи ЛП, обозначаемые через ЛП-2 и ЛП-3. Они получаются путем введения ограничений 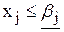 и
и 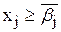 соответственно, где через
соответственно, где через 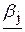 обозначается наибольшее целое, не превосходящее bj , через
обозначается наибольшее целое, не превосходящее bj , через 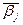 - наименьшее целое, большее
- наименьшее целое, большее 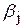 . Условия задачи ЛП-2 и ЛП-3 можно записать следующим образом:
. Условия задачи ЛП-2 и ЛП-3 можно записать следующим образом:
ЛП-2 ЛП-3
Максимизировать Z=СX Максимизировать Z=CX
при ограничениях AX=B, при ограничениях AX=B,
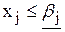
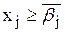
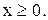
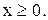
Допустим, что оптимальные решения задач ЛП-2 и ЛП-3 также содержат дробные значения целочисленных переменных и поэтому не являются допустимыми для исходной задачи.
На следующем шаге необходимо выбрать задачу ЛП-2 или ЛП-3 и произвести ветвление в соответствующей вершине, вводя новое ограничение. Выбор вершины (задачи ЛП) для дальнейшего ветвления осуществляется с помощью специальных правил. Приведем некоторые из них.
1. Использование оптимального значения целевой функции. Для дальнейшего ветвления следует выбирать вершину, соответствующую наибольшему оптимальному значению целевой функции задачи ЛП. Некоторым обоснованием этого правила служит то соображение, что допустимая область задачи ЛП с наибольшим значением Z может содержать и хорошее целочисленное решение. Например, любое целочисленное решение, полученное ветвлением задачи ЛП-2, не может давать значение Z, лучше, чем оптимальное значение Z в задаче ЛП-2.
2. Правило "последним пришел - первым обслужен". Для дальнейшего ветвления выбирается (произвольным образом) задача ЛП, решавшаяся последней.
После выбора вершины для дальнейшего ветвления выбирается целочисленная переменная, которая имеет в оптимальном решении соответствующей задачи ЛП дробное значение, и производится ветвление по этой переменной. Процесс ветвления и решения задачи продолжается до получения целочисленного оптимального решения одной из задач ЛП. Значение Z в полученной точке представляет собой нижнюю границу оптимального значения целевой функции исходной задачи ЦЛП. На этом этапе определяются прозондированные вершины, т.е. вершины, в которых дальнейшее ветвление невозможно или нецелесообразно. Вершина является прозондированной, если она удовлетворяет одному из следующих условий:
1.Оптимальное решение, соответствующее данной вершине, целочисленно. В этом случае полученное решение допустимо для исходной задачи ЦЛП.
2. Задача ЛП, соответствующая рассматриваемой вершине, не имеет допустимых решений.
3. Оптимальное значение Z соответствующей задачи ЛП не превосходит текущей нижней границы.
Во втором и третьем случаях прозондированные вершины отбрасываются. Процесс решения задачи продолжается до тех пор, пока все вершины не будут прозондированы. Прозондированная вершина, соответствующая целочисленному решению с наилучшим (наибольшим) значением целевой функции дает оптимальное решение исходной задачи.
Пример . Для иллюстрации основных принципов метода ветвей и границ рассмотрим следующую задачу целочисленного программирования.
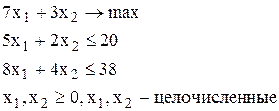
Начальный шаг решения этой задачи состоит в нахождении решения задачи линейного программирования, получаемой при отбрасывании условия целочисленности x1 и x2. Обозначим эту задачу через ЛП-1. Ее оптимальное решение имеет вид x1=1, x2=7.5, оптимальное значение целевой функции Z1=29.5. Поскольку x2 принимает дробное значение, найденное решение не может быть оптимальным решением исходной целочисленной задачи. Найденное значение Z1 представляет собой верхнюю границу истинного оптимального целочисленного значения, поскольку при выполнении требования целочисленности x2 значение Z может лишь уменьшиться.
Следующий шаг метода ветвей и границ состоит в разбиении задачи ЛП-1 на две подзадачи , первая из которых (ЛП-2) образуется в результате добавления к задаче ЛП-1 ограничения 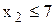 , а вторая (ЛП-3) - в результате добавления ограничения
, а вторая (ЛП-3) - в результате добавления ограничения 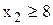 :
:
ЛП-2 ЛП-3
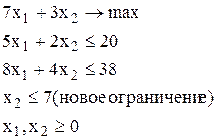
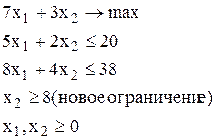
Дерево возможных вариантов представлено на рис. 33. Оптимальное решение задачи ЛП-3 - точка х1=0.75, х2=8, где Z2=29,25. Оптимальное решение задачи ЛП-2 точка х1=1.2, х2=7, где Z3=29,4. Для дальнейшего ветвления выберем задачу ЛП-2, т.к. значение целевой функции в ней больше. К задаче ЛП-2 добавим ограничения 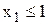 , (задача ЛП-4) и
, (задача ЛП-4) и 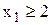 (задача ЛП-5). Результаты решения задачи ЛП-4: х1=1, х2=7, где Z4=28. Результаты решения задачи ЛП-5: х1=2, х2=5, где Z5=29.
(задача ЛП-5). Результаты решения задачи ЛП-4: х1=1, х2=7, где Z4=28. Результаты решения задачи ЛП-5: х1=2, х2=5, где Z5=29.
Таким образом, получены два допустимых (целочисленных) решения исходной задачи целочисленного программирования, причем значение Z4=29 представляет собой нижнюю границу максимального значения Z для задачи целочисленного программирования. Даже если исходная задача имеет другие целочисленные решения, значение целевой функции в них не может быть больше 29. Таким образом, значение Z4=29 представляет собой нижнюю границу максимального значения Z для исходной целочисленной задачи. Вершины ЛП-4 и ЛП-5 являются прозондированными (так как в них получено целочисленное решение, а в процессе дальнейшего ветвления оно может лишь ухудшаться). Ветвление вершины ЛП-3 также нецелесообразно в связи с тем, что целевая функция исходной задачи может принимать только целочисленные значения (т.к. все переменные и коэффициенты целочисленны), а при дальнейшем ветвлении ее значения будут увеличиваться (т.е., станут больше 29). Следовательно, оптимальное решение задачи х1=2, х2=5, где Z5=29.
Метод ветвей и границ может применяться для решения не только линейных, но и нелинейных целочисленных задач. Он также может использоваться для решения задач с дискретными переменными.

|
Основные стратегии метода ветвей и границ.
Методы ветвей и границ - не один специальный алгоритм, а широкий класс алгоритмов. Эффективность конкретного алгоритма в рамках данного класса задач зависит от выбранной стратегии его формирования для рассматриваемой задачи.
1. Выбор вершины (подзадачи) для ветвления. Возможны следующие стратегии:
a) Выбирается вершина с минимальной нижней оценкой.
б) Поиск в глубину: всегда выбирается одна из новых, только что полученных подзадач (Last In First Out).
в) Поиск в ширину: стратегия FIFO.
2. Выбор нецелочисленной переменной, по которой осуществляется ветвление и которая определяет дополнительные ограничения:
1) Выбирается переменная с максимальной дробной частью
2) Переменным приписываются приоритеты и ветвление осуществляется по переменной с максимальным приоритетом. Выбор приоритета может осуществляться следующими соображениями:
a) Коэффициент целевой функции при данной переменной больше остальных
б) Данная переменная является наиболее важной, ее значение играет ключевую роль в модели по мнению разработчиков.
3) Находится то дополнительное ограничение, которое приводит к наибольшему возрастанию нижней границы. Цель - найти ту вершину, которая наиболее верно будет отброшена.
4) Переменная для ветвления выбирается произвольным образом, например, переменная с минимальным номером.
3. Вычисление нижней границы. Имеется выбор между границами, которые относительно точны, но требуют большего времени вычисления и границами, которые не столь точны, но которые могут быстро вычислиться. Для задач целочисленного программирования специального вида (задача коммивояжера, задача о ранце) разработаны специальные методы вычисления нижних границ.
4. Вычисление верхних границ.
а) Верхние границы специально не вычисляются, а определяются в процессе решения при получении целочисленного результата.
б) Верхние границы вычисляются перед началом работы МВГ с помощью какого-либо эвристического алгоритма.
в) Вычисление верхних границ с помощью эвристических процедур осуществляется на каждом шаге работы алгоритма (для каждой подзадачи).
б) и в) требуют дополнительных вычислительных затрат, но позволяет более эффективно сократить перебор.
Четких рекомендаций по выбору стратегии в МВГ нет, он зависит от конкретных условий решаемой задачи.
Нелинейная оптимизация.
В общем виде задача нелинейной оптимизации может быть сформулирована следующим образом:
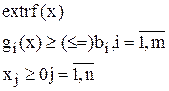 (1)
(1)
Задача (1) называется нелинейной, если хоть одна их функций f(x) или 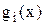 будет нелинейной. В ЗНП могут присутствовать также ограничения типа равенств.
будет нелинейной. В ЗНП могут присутствовать также ограничения типа равенств.
ЗНП без ограничений.
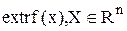 (2) - задача безусловной оптимизации.
(2) - задача безусловной оптимизации.
ЗНП, в которой присутствуют ограничения только в виде равенств и отсутствует условие неистинности переменных, называется задачей на условный экстремумили классической задачей оптимизации.
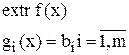 . (3)
. (3)
Область допустимых решений в ЗПН может быть выпуклой или невыпуклой.
ЗНП, связанная с минимизацией (максимизацией) вогнутой (выпуклой) функции f(x), которая задана на выпуклой области D, называется задачей выпуклого программирования.
Функция f(x) называется вогнутой (выпуклой), если ее график нигде не лежит под (над) касательной к нему.
Условия:
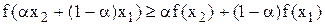
(для выпуклой функции)
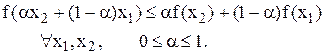
(для вогнутой функции) или
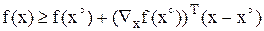
Условия оптимальности для ЗНП.
1. Условие оптимальности для задачи безусловного оптимизации функции одной переменной:
Необходимое условие:
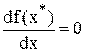 .
.
Достаточное условие:
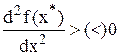 .
.
Больше нуля - для минимума, меньше - для максимума.
(Если равно 0 продолжать брать производную до тех пор, пока не будет 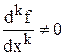 . Если к нечетное, экстремума нет. Если к четное, то аналогично второй производной.)
. Если к нечетное, экстремума нет. Если к четное, то аналогично второй производной.)
2. Условие оптимальности для задачи оптимизации функции одной переменной при дополнительном условии неотрицательности этой переменной 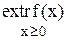 .
.
Необходимое условие 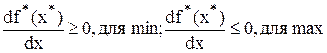 .
.
Достаточное условие 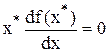 .
.
3. Для задачи безусловной оптимизации функции нескольких переменных 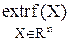 .
.
Необходимое условие 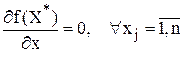 .
.
Достаточное условие: в точке X* матрица вторых производных (матрица Гессе) должна быть положительно определена (для минимума) или отрицательно ( для максимума).
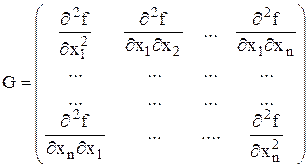
Условие минимума 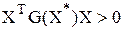 ,
, 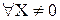 - для отрицательно определенной матрицы.
- для отрицательно определенной матрицы.
4. Если к задаче (3) добавить условия неотрицательности всех переменных 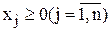 , то необходимое условие экстремума:
, то необходимое условие экстремума:
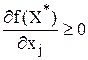 для минимума и меньше нуля - для максимума;
для минимума и меньше нуля - для максимума;
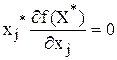 .
.
5. Условие оптимальности для задачи на условный экстремум.
Условие может быть получено с помощью метода множителей Лагранжа. Введем набор переменных 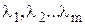 , называемых множителями Лагранжа и составляющих функцию Лагранжа:
, называемых множителями Лагранжа и составляющих функцию Лагранжа:
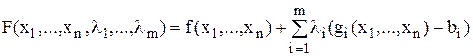 , где
, где 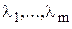 - произвольные действительные числа. Затем находятся частные производные
- произвольные действительные числа. Затем находятся частные производные 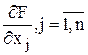 и
и 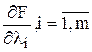 , и рассматривается система n+m уравнений с n+m неизвестными, в которых каждая производная приравнивается нулю.
, и рассматривается система n+m уравнений с n+m неизвестными, в которых каждая производная приравнивается нулю.
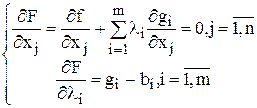
Решив систему, получим точки, которые могут быть оптимальны. Дальнейшее исследование осуществляется также, как и в случае безусловного экстремума.
6. Условие оптимальности для задачи выпуклого программирования.
Рассмотрим задачу выпуклого программирования:
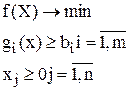 .
.
Определение. Множество дополнительных решений задачи ЗВП удовлетворяет условиям регулярности, если для любой i 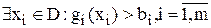 . Каждый локальный минимум или максимум ЗВП является и глобальным.
. Каждый локальный минимум или максимум ЗВП является и глобальным.
Для учета ограничений ЗВП осуществляется переход к задаче без этих ограничений путем введения штрафа за их нарушение. Для этого на множестве 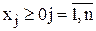 вводится штрафная функция Лагранжа:
вводится штрафная функция Лагранжа:
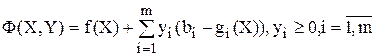 , где yi называются штрафными множителями Лагранжа.
, где yi называются штрафными множителями Лагранжа.
Таким образом при нарушении ограничения осуществляется увеличение целевой функции, т.е. производится штраф за нарушение ограничения. Величина штрафа определяется переменными yi.
В терминах функции Лагранжа исходную задачу можно записать:
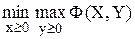 .
.
Задачу 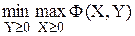 называется двойственной задачей к исходной задаче.
называется двойственной задачей к исходной задаче.
Точка (X*,Y*) называется седловой точкой функции Лагранжа, если выполняется следующее условие:
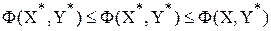
или
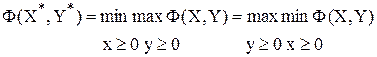
Теорема Куна-Таккера.
Для задачи выпуклого программирования, множество допустимых решений которой обладает свойством регулярности, точка X* является оптимальной тогда и только тогда, когда существует такая 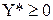 ,что пара (X*,Y*) является седловой точкой функции Лагранжа.
,что пара (X*,Y*) является седловой точкой функции Лагранжа.
Дифференциальный вариант теоремы Куна-Таккера (необходимое и достаточное условие экстремума для ЗВП).
Для того, чтобы пара (X*,Y*) была седловой точкой функции Лагранжа, необходимо и достаточно выполнение следующих условий:
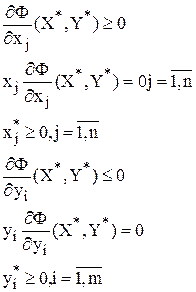
Условия теоремы не дают вычислительного алгоритма для определения оптимального решения. Они могут быть использованы для проверки точек, подозреваемых на экстремум. Иногда возможно исключение из допустимой области тех множеств точек, для которых удается показать, что ни один их элемент не может удовлетворять условию оптимальности.
Пример:
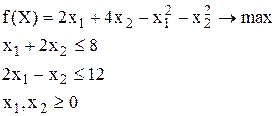
проверить, являются ли точки 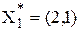 и
и 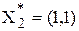 оптимальным решением заданной задачи.
оптимальным решением заданной задачи.
а) Составим функцию Лагранжа
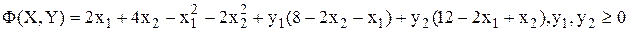 .
.
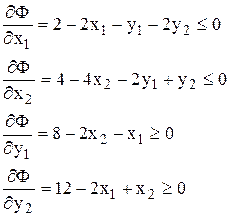
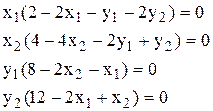
Т. е. X1*=(2,1) не является решением, а X2*=(1,1) - является.
Cведение задач с ограничениями к задачам безусловной оптимизации.
Одним из наиболее распространенных приемов решения нелинейных задач с ограничениями является их сведение к задачам безусловной оптимизации. При этом учет прямых и функциональных ограничений моет осуществляться по разному.
1. Учет прямых ограничений
Исключение прямых ограничений на варьируемые параметры может быть осуществлено с использованием замены переменных.
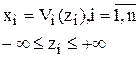 , где n - число варьируемых параметров, на которые наложены прямые ограничения. Zi - новые варьируемые параметры.
, где n - число варьируемых параметров, на которые наложены прямые ограничения. Zi - новые варьируемые параметры.
Тогда задача с прямыми ограничениями и целевой функцией f(x) сводится к задаче безусловной оптимизации следующего вида:
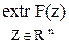 , где
, где 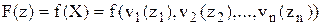 .
.
Примеры:
1) 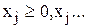 тогда может быть использована замена переменной
тогда может быть использована замена переменной 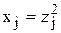 .
.
2) 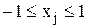 , тогда
, тогда 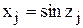
3) 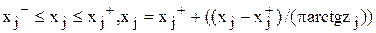
2. Учет функциональных ограничений.
Для учета функциональных ограничений обычно используется метод штрафных функций. При этом решение задач с ограничениями сводится к решению последовательностей задач безусловной оптимизации. В общем виде такое преобразование осуществляется при помощи специальным образом сконструированной функции H(X), называемой штрафной функцией или функцией штрафа. В результате мы переходим к следующей целевой функции: Ф(X)=f(x)+H(x).
Существует два подхода к построению штрафных функций:
1. Методы внутренних штрафных функций (барьерных функций).
2. Методы вешних штрафных функций.
2.1.Методы внутренних штрафных функций.
Эти методы арактеризуются следующими функциями штрафа:
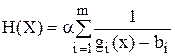 (1)
(1)
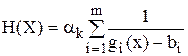 (2)
(2)
где альфа - параметр штрафа, значение параметра может быть постоянным (случай 1) или меняться на различных итерациях (случай 2).
В случае 2 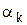 выбирается таким образом, чтобы его значения стремилось к нулю при
выбирается таким образом, чтобы его значения стремилось к нулю при 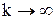 .
.
В данном случае поиск минимума следует начинать с внутренней точки допустимой области, то есть с точки, в которой все ограничения выполнены, как строгие неравенства. При выходе на границу допустимой области штраф будет бесконечным, следовательно, оптимизационный процесс никогда не выйдет за пределы допустимой области.
Недостатком таких штрафных функций является то, что они требуют существования внутренних точек дополнительной области D, т.е. не позволяют решать ЗНП с ограничениями типа равенств. Кроме того, для их использования необходимо знать начальную допустимую точку.
2.2. Метод внешних штрафных функций.
Функции штрафа при этом может иметь следующий вид:
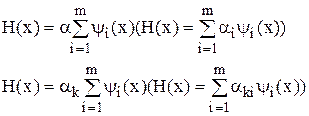
В первом случае параметр a одинаков на всех итерациях.
Во втором случае 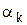 изменяется в процессе поиска таким образом, чтобы при приближении к оптимальной точке влияние функции штрафа постепенно ослабевало, а
изменяется в процессе поиска таким образом, чтобы при приближении к оптимальной точке влияние функции штрафа постепенно ослабевало, а 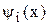 может иметь следующий вид:
может иметь следующий вид:
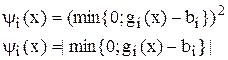
Таким образом, если ограничение не нарушается, т.е. 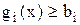 , то
, то 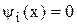 à H(X)=0.
à H(X)=0.
Если ограничение нарушается, то величина штрафа зависит от степени нарушаемого ограничения. Таким образом, ЗНП с ограничениями могут быть сведены к задачам безусловной оптимизации, следовательно, алгоритмы безусловной оптимизации составляют инвариантную часть алгоритмического обеспечения, предназначенного для решения оптимизационных задач. При этом учет ограничений осуществляется на внешнем уровне и не затрагивает инвариантное алгоритмическое ядро.
Алгоритмы безусловной оптимизации.
Рассмотрим задачу безусловной оптимизации вида
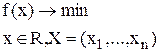
В общем виде алгоритмы безусловной оптимизации являются итерационными процедурами, реализующими последовательное приближение к данному экстремуму.
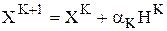 ,
,
где k - номер итерации, HК - направление движения на k-й итерации, 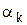 - величина шага в этом направлении. При этом:
- величина шага в этом направлении. При этом:
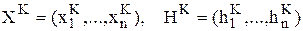
Получаемая последовательность точек  называется траекторией поиска и должна сходиться к оптимальной точке X*. Таким образом, алгоритмы безусловной оптимизации различаются по способам выбора направлений поиска
называется траекторией поиска и должна сходиться к оптимальной точке X*. Таким образом, алгоритмы безусловной оптимизации различаются по способам выбора направлений поиска 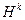 и величины шага, причем способ выбора направления поиска является определяющим.
и величины шага, причем способ выбора направления поиска является определяющим.
В зависимости от способа выбора направления поиска h методы безусловной оптимизации делятся на методы 0-го, 1-го и 2-го порядка.
а) Методы 0-го порядка - методы, в которых для определения направления поиска используются только значения целевой функции. Производные в данном случае не вычисляются.
Эти методы также называют поисковыми методами оптимизации. К ним относятся методы переменного многогранника и различные методы покоординатного поиска.
Особенностью методов поисковой оптимизации является то, что они могут быть использованы при алгоритмическом задании критериев оптимальности и ограниченности.
б) Методы первого порядка - методы, в которых для определения направления поиска используются 1-е производные целевой функции по параметру. Эти методы называют также градиентными.
в) Методы 2-го порядка - это методы, в которых для определения направления поиска используются 2-е производные целевой функции. К этому классу относят метод Ньютона и его модификации.
Важной характеристикой методов является их скорость сходимости. Скорость сходимости линейна:
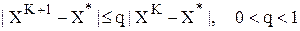 , где X* - точка минимума.
, где X* - точка минимума.
Скорость сходимости сверхлинейна, если 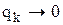 при
при 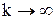 .
.
Скорость сходимости квадратична, если 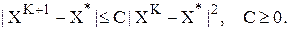
Точность результата может оцениваться величиной 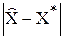 , где
, где 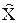 – решение задачи.
– решение задачи.
Рассмотрим методы 1-го и 2-го порядка. Для формирования правила перехода из одной точки траектории поиска в другую 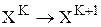 воспользуемся аппроксимацией целевой функции в окрестности точки ХК с использованием формулы Тейлора
воспользуемся аппроксимацией целевой функции в окрестности точки ХК с использованием формулы Тейлора
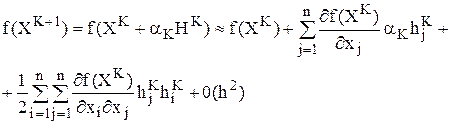
В векторной форме:
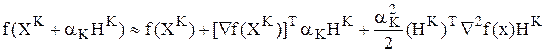
Градиентные методы оптимизации
Воспользовавшись линейной аппроксимацией целевой функции, получим
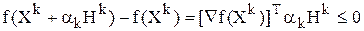
Это неравенство всегда выполняется, если в качестве направления 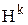 можно выбрать антиградиент
можно выбрать антиградиент 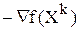 . Известно, что градиент функции является направлением ее наискорейшего возрастания, а антиградиент - направлением наискорейшего убывания. Таким образом, получим следующую итерационную процедуру поиска:
. Известно, что градиент функции является направлением ее наискорейшего возрастания, а антиградиент - направлением наискорейшего убывания. Таким образом, получим следующую итерационную процедуру поиска:
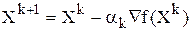
В координатной форме:
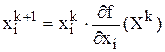
Итерационные процедуры, в которых направление движения на каждой итерации совпадает с антиградиентом (градиентом) целевой функции, называются градиентными методами и отличаются друг от друга способами выбора шага ak .
1. Градиентные методы с постоянным шагом. При этом величина шага задается на начальной итерации и в процессе поиска не меняется.
2. Градиентные методы с дроблением шага. В этих методах выбирается на начальном этапе поиска произвольное значение шага aо . На каждой последующей итерации проверяется выполнение неравенства
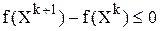 .
.
Если неравенство не выполняется, то осуществляется дробление шага ak до тех пор, пока оно не станет истинным.
Может быть использовано более жесткое условие:
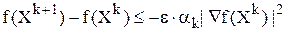 ,
,
где 0 < e < 1 - константа, неизменяемая на всех итерациях.
Смысл этих условий : функция должна убывать от итерации к итерации.
 |
Геометрическая интерпретация градиентных методов:
Градиент направлен перпендикулярно касательной к линии уровня целевой функции в каждой точке. Очевидно, что сходимость градиентных методов наиболее высока, когда ЛУЦФ имеют вид концентрических окружностей.
3. Метод наискорейшего спуска
В этом методе на каждой итерации определяется оптимальная длина шага в результате решения вспомогательной задачи одномерной оптимизации.
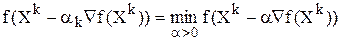
 |
Таким образом, шаг градиентного метода(переход на новую точку поиска) чередуется с этапом определения оптимальной длины шага. Как правило, этот метод более эффективен, чем предыдущий, так как обеспечивает движение с самым выгодным шагом, однако его трудоемкость выше, чем в рассматриваемых ранее методах.
В этом методе, в отличие от обычного градиентного спуска, направление движения из точки Х k касается линии уровня в точке Х k+1 . Последовательность точек Х 0 ,Х 1 … Х k ,…зигзагообразно приближается к точке минимума, причем звенья этого зигзага ортогональны между собой.
Действительно, шаг a выбирается из условия минимизации по a функции
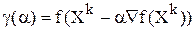 , поэтому
, поэтому
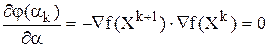
Градиентные методы обладают линейной скоростью сходимости
Достоинства: простота и широта использования (универсальность).
Недостатки: если линии уровня имеют овражный характер, то эти методы плохо сходятся. Это бывает, если матрица двух производных (матрица Гессе) плохо обусловлена, то есть ее максимальное М и минимальное m собственные числа сильно отличаются друг от друга.
В этом случае необходимо использовать вторые производные целевой функции для построения методов, которые не реагируют на овражную структуру f(X).
Методы второго порядка.
Для определения направления поиска Hk воспользуемся квадратной аппроксимацией целевой функции в окрестности точки xk, получим:
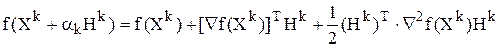
Используем необходимое условие экстремума
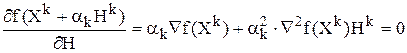
Отсюда
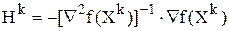 - направление поиска.
- направление поиска.
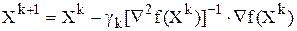 ,
,
где 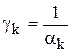
Процедуры такого типа называют процедурами Ньютона.
Различают:
1) Стандартный, классический метод Ньютона (длина шага на всех итерациях равна единице)
2) Метод Ньютона с регулировкой шага. ( 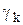 меняется на каждой итерации).
меняется на каждой итерации).
Метод Ньютона без регулировки шага сходится лишь при удачном выборе начального приближения. Методы с регулировкой шага сходятся независимо от начальной точки и обладают либо сверхлинейной, либо квадратичной скоростью сходимости.
Рассмотрим два способа выбора длинны шага ak . Первый связан с проверкой неравенства, аналогичного тому, что рассматривалось в градиентном методе:
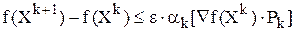 ,
,
где 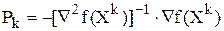 и 0<e <1/2
и 0<e <1/2
Второй способ определения шага аналогичен методу наискорейшего спуска и состоит в минимизации функции 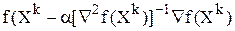 по a в направлении движения.
по a в направлении движения.
(*) Целевая функция F(x) непосредственно или косвенно связана с выходными параметрами проецируемого объекта. Рассмотрим основные виды критерием оптимизации.
1. Самый простой случай – когда в качестве критерия оптимальности выбирается сами выходные параметры. 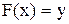 или
или
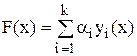 ,
,
где n – число выходных параметров, ai - весовой коэффициент, задающий относительную важность выходного параметра yi (x) по сравнению с другими.
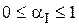
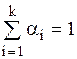
2. Критерий оптимальности связан с выходными характеристиками функциональной зависимостью: 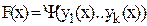
3. Для отображения степени близости оптимизируемых параметров желаемых или нежелаемых значениям часто используются критерии вида:
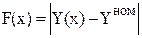 или
или 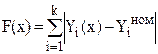
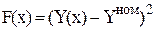 или
или 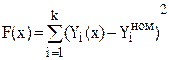
Замечание. Разнообразие и сложность реальных практических задач оптимизации не позволяет ограничиваться одним критерием оптимальности. Обычно реальные практические задачи многокритериальны, т.е. имеется целый набор показателей, характеризующий тот или иной вариант объекта. Часто эти критерии бывают противоречивыми.
Существует большое число методов и алгоритмов многокритериальной (векторной) оптимизации, однако все они в конечном итоге сводятся к оптимизации по одному критерию.
Рассмотрим некоторые такие подзадачи.
а) Вычисление наиболее приемлемого критерия с номером m и перевод остальных критериев в систему ограничений: 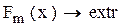
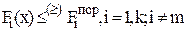 , где
, где
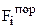 - некоторое устанавливаемое разработчиком пороговое
- некоторое устанавливаемое разработчиком пороговое
значение критерия.
б) Составление некоторого обобщенного критерия, включающего в себя все частные критерии (аддитивная свертка)
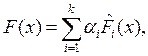
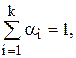
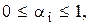
где 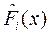 - нормированные частные критерии оптимальности, приведенные к безразмерному виду.
- нормированные частные критерии оптимальности, приведенные к безразмерному виду.
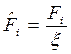 , где x - константа, равная единице измерения величины Fi
, где x - константа, равная единице измерения величины Fi
или 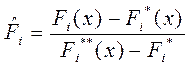
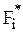 - некоторое min значение критерия в области компромисса
- некоторое min значение критерия в области компромисса
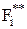 - max значение в области компромисса.
- max значение в области компромисса.
Методы решения задач многокритериальной оптимизации будут рассматриваться в следующем семестре. Но так как любую многокритериальную задачу можно свести к однокритериальной, мы будем в дальнейшем рассматривать задачи с одним критерием оптимальности.
Дата добавления: 2017-05-18; просмотров: 1466;
