Задача о назначениях.
Линейная задача о назначениях .
Имеется n исполнителей и n видов работ, которые они могут выполнять. Пусть 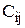 - производительность i-го исполнителя при выполнении j работы. Каждый исполнитель может выполнять один вид работ, а каждый вид работ может быть выполнен одним исполнителем. Требуется таким образом распределить исполнителей по видам работ, чтобы общая производительность была максимальной.
- производительность i-го исполнителя при выполнении j работы. Каждый исполнитель может выполнять один вид работ, а каждый вид работ может быть выполнен одним исполнителем. Требуется таким образом распределить исполнителей по видам работ, чтобы общая производительность была максимальной.
Введем альтернативные переменные 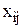 :
:
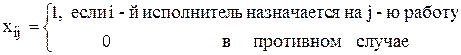
Тогда математическая модель задачи имеет вид:
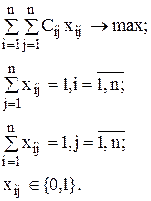
Иногда задача о назначениях формулируется как задача минимизации, если в качестве 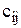 выбирается время, затраченное i-м исполнителем на выполнение j-й работы.
выбирается время, затраченное i-м исполнителем на выполнение j-й работы.
Необходимо заметить, что условие целочисленности переменных в задаче о назначениях можно не накладывать, т.к. эта задача является частным случаем транспортной задачи и при целочисленности правых частей ограничений целочисленность решения обеспечивается автоматически.
К задаче о назначениях сводится широкий круг задач дискретной оптимизации (распределение исполнителей по видам работ, закрепление за станками операций, распределение задач между различными ЭВМ, назначение претендентов на вакантные должности при формировании штатного расписания и т.д).
Пример . При передаче сообщений по каналу с шумом необходимо каждой букве передаваемого алфавита поставить в соответствие букву принимаемого таким образом, чтобы сумма вероятностей правильности принимаемых букв была бы максимальна.
Пусть 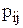 - вероятность соответствия принимаемой j-й буквы передаваемой i-й букве. Введем альтернативные переменные:
- вероятность соответствия принимаемой j-й буквы передаваемой i-й букве. Введем альтернативные переменные:
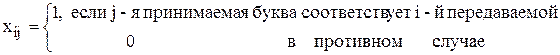
Тогда математическая модель задачи будет иметь следующий вид:
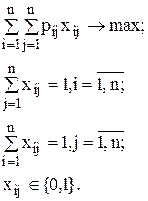
Квадратичная задача о назначениях.
Имеется m пунктов, в которых необходимо разместить n объектов. В каждом пункте может быть размещен только один объект. Даны расстояния между i-м и j-м пунктами 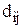 , а также csk – показатели, характеризующие взаимосвязи между s-м и k-м объектами (стоимость перевозок, число коммукникаций и т.д.). Необходимо определить такое назначение объектов в выделенные пункты, чтобы минимизировать соответствующие затраты.
, а также csk – показатели, характеризующие взаимосвязи между s-м и k-м объектами (стоимость перевозок, число коммукникаций и т.д.). Необходимо определить такое назначение объектов в выделенные пункты, чтобы минимизировать соответствующие затраты.
Математическая модель задачи имеет следующий вид:
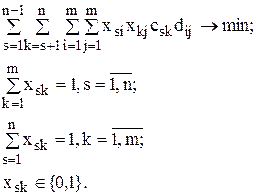
В данном случае целевая функция зависит не от всевозможных назначений, а от всевозможных пар назначений (s-й элемент размещается в i-й пункт, а k-й – в j-й пункт). Целевая функция при этом не является линейной.
Квадратичная задача о назначениях имеет широкий круг практических приложений. Она может быть использована для решения задач размещения (оборудования, предприятий, деталей, и т.д.). Особенно часто эта модель используется в задачах конструкторско-топологического проектирования.
Пример. Необходимо таким образом разместить n компонентов печатной платы на m позициях монтажного пространства, чтобы суммарная длина электрических соединений между компонентами была бы минимальной.
Предположим, что n=m. Пусть 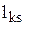 - расстояние между k-й и s-й позициями,
- расстояние между k-й и s-й позициями, 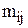 - число связей между i-м и j-м компонентами. Введем бинарные переменные
- число связей между i-м и j-м компонентами. Введем бинарные переменные
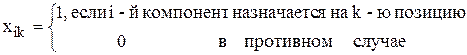 .
.
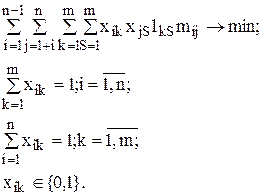
Дата добавления: 2017-05-18; просмотров: 897;
