Особый класс задач с неделимостями составляют целочисленные ТЗ, в которых целочисленные решения обеспечиваются при целочисленности исходных данных.
Переход от задач с дискретными переменными к целочисленным задачам
1. Изменение масштаба.
2. Преобразование системы ограничений:
а) пусть 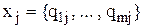
Введем бинарную переменную yij, принимающую значения 0, 1.
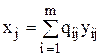 , при условиях
, при условиях
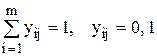 .
.
То есть мы перешли от произвольных дискретных переменных к бинарным.
б) аналогично можно преобразовать задачу целочисленного программирования в задачу с бинарными переменными, если 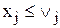 .
.
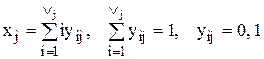
Поэтому в дальнейшем будем рассматривать задачи с целочисленными переменными.
- задачи с альтернативными переменными (или с логическими условиями). В этих задачах вводятся искусственные альтернативные переменные, отражающие логические условия задачи. Это задачи с дополнительными логическими условиями (“или-или”, “если, то”).
Наиболее распространенными являются задачи целочисленного программирования, так как любую дискретную задачу можно привести к целочисленной.
Прикладные дискретные модели
Задача о раскрое.
Для изготовления заготовок D1,…,Dm имеется n способов раскроя материала A1,…,An. 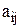 -количество заготовок i-го типа, получаемых из единицы материала при способе Aj. Имеется D единиц материала. При раскрое единицы материала по способу Aj имеются отходы площадью
-количество заготовок i-го типа, получаемых из единицы материала при способе Aj. Имеется D единиц материала. При раскрое единицы материала по способу Aj имеются отходы площадью 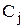 . Надо произвести не менее
. Надо произвести не менее 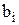 заготовок i-го типа и выполнить план с минимизацией отходов.
заготовок i-го типа и выполнить план с минимизацией отходов.
Таблица 11
| Виды заготовок | Способы раскроя | План производства | |||
| A1 | A2 | … | An | ||
| D1 D2 … Dm | A11 a21 ... am1 | a12 a22 ... am2 | ... ... ... ... | a1n a2 n ... amn | b1 b2 ... bm |
| Отходы | C1 | c2 | … | cn |
Пусть 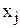 - количество единиц материала, раскраиваемого по j-му способу.
- количество единиц материала, раскраиваемого по j-му способу.
Математическая модель задачи запишется следующим образом:
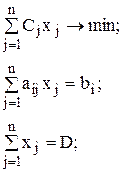
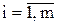 ;
;
.
Задача о ранце. Имеются предметы n видов, для каждого предмета j-го вида (j=1,n) известны его объем 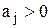 и стоимость
и стоимость 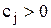 . Необходимо определить такой набор предметов, суммарный объем которых не превышал бы заданного числа b, а суммарная ценность была бы максимальной. Эта задача интерпретируется как задача загрузки ранца объема b и называется одномерной задачей о ранце.
. Необходимо определить такой набор предметов, суммарный объем которых не превышал бы заданного числа b, а суммарная ценность была бы максимальной. Эта задача интерпретируется как задача загрузки ранца объема b и называется одномерной задачей о ранце.
Введем целочисленные переменные 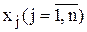 , значения которых характеризует количество предметов j-го вида, помещенных в ранец. Тогда математическая модель данной задачи имеет вид:
, значения которых характеризует количество предметов j-го вида, помещенных в ранец. Тогда математическая модель данной задачи имеет вид:
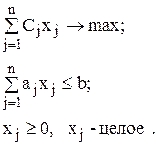
Если ограничениями могут быть не только объем ранца, но и другие его характеристики 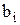 , то получим многомерную задачу о ранце.
, то получим многомерную задачу о ранце.
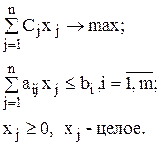
В случае, если количество предметов j-го вида ограничено и равно 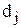 , к задаче добавляется ограничение
, к задаче добавляется ограничение 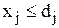 . Если
. Если 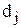 =1, то получим задачу о ранце с булевыми переменными. Тогда
=1, то получим задачу о ранце с булевыми переменными. Тогда 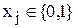 , причем
, причем 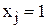 , если j-й предмет помещен в ранец,
, если j-й предмет помещен в ранец, 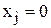 в противном случае.
в противном случае.
К задаче о ранце сводится широкий класс задач дискретной оптимизации с ограниченными ресурсами.
Пример. Для оценки работоспособности систем перед их эксплуатацией производится проверка их функционирования. При проверке контролируются отдельные параметры системы, каждый из которых характеризуется вероятностью отказа проверяемых элементов 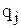 и временем контроля
и временем контроля 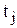 . Так как допустимое время контроля всей системы T ограничено, то для проверки необходимо выбрать параметры, контролирующие наиболее ненадежные элементы и требующие для контроля наименьшего времени.
. Так как допустимое время контроля всей системы T ограничено, то для проверки необходимо выбрать параметры, контролирующие наиболее ненадежные элементы и требующие для контроля наименьшего времени.
Пусть n – общее количество параметров. Введем альтернативные булевы переменные:
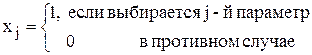
Тогда математическую модель задачи можно сформулировать как одномерную задачу о ранце:
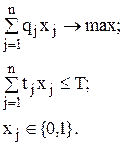
Дата добавления: 2017-05-18; просмотров: 364;
