Преобразование логических функций
В задачи преобразования ФАЛ входят их минимизация различными способами, перевод функций из одной формы в другую, приведение их к различным базисам, инверсия функций и т. п.
Способы минимизации рассмотрены в предыдущем разделе. Там же сказано, что каноническими формами представления функций алгебры логики являются СДНФ и СКНФ. В практике часто возникает необходимость перехода из одной формы в другую. При этом, если функция задана таблицей истинности, то СДНФ можно получить сразу, если мы комбинации аргументов, при которых функция принимает значения I, представим в виде конъюнкций и соединим их знаками дизъюнкций.
СКНФ получим, если комбинации аргументов, при которых функция равна 0, представим в виде дизъюнкций инверсий этих аргументов, соединенных знаками конъюнкции.
Пример. Функция задана таблицей истинности (табл. 5).
Таблица 5- Истинность ФАЛ трёх аргументов
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| f |
Тогда СДНФ функции, когда f = 1
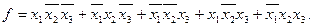
СКНФ этой же функции, когда f = 0
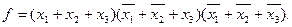
Пользуясь приведенным примером, можно сформулировать правила перехода от СДНФ к СКНФ и наоборот, если функции в той или другой форме записаны в виде алгебраического выражения. Для перехода от СДНФ к СКНФ необходимо записать в виде СДНФ недостающие комбинации аргументов и полученное выражение проинвертировать.
Пример. Пусть задана СДНФ функции
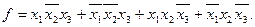
Требуется данную функцию выразить в СКНФ.
Недостающими комбинациями аргументов являются:
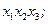
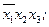
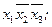
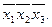
Запишем их в виде СДНФ и проивертируем полученное выражение:
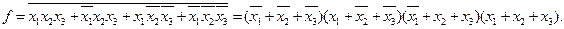
В результате получим заданную функцию в СКНФ.
Пример. Если заданна функция в СКНФ:
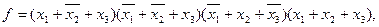
то в этом случае недостающее до полного набора комбинации аргументов записываются в форме СКНФ и полученное выражение инвертируется:
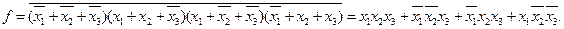
Таким образом, осуществлен переход от СКНФ к СДНФ.
Дата добавления: 2017-04-20; просмотров: 741;
