Максвелл ввел понятие полного тока,равного сумме токов проводимости (а также конвекционных токов) и смещения.Плотность полного тока 20 страница

Энергия внешних электронов может принимать значения в пределах закрашенных на рис. 313 областей, называемыхразрешенными энергетическими зонами. Каждая разрешенная зона «вмещает» в себя столько близлежащих дискретных уровней, сколь­ко атомов содержит кристалл: чем больше в кристалле атомов, тем теснее рас­положены уровни в зоне. Расстояние между соседними энергетическими уровнями в зоне составляет приблизительно 10^–22 эВ. Так как оно столь ничтожно, то зоны можно считать практически непрерывными, однако факт конечного числа уровней в зоне играет важную роль для распределения электронов по состояниям.

Разрешенные энергетические зоны разделены зонами запрещенных значений энер­гии, называемымизапрещенными энергетическими зонами. В них электроны находиться не могут. Ширина зон (разрешенных и запрещенных) не зависит от размера кристалла. Разрешенные зоны тем шире, чем слабее связь валентных электронов с ядрами.

§ 241. Металлы, диэлектрики и полупроводники по зонной теории

Зонная теория твердых тел позволила с единой точки зрения истолковать существова­ние металлов, диэлектриков и полупроводников, объясняя различие в их электрических свойствах, во-первых, неодинаковым заполнением электронами разрешенных зон и, во-вторых, шириной запрещенных зон.

Степень заполнения электронами энергетических уровней в зоне определяется заполнением соответствующих атомных уровней. Если при этом какой-то энергетичес­кий уровень полностью заполнен, то образующаяся энергетическая зона также запол­нена целиком. В общем случае можно говорить о валентной зоне, которая полностью заполнена электронами и образована из энергетических уровней внутренних электро­нов свободных атомов, и о зоне проводимости (свободной зоне), которая либо частично заполнена электронами, либо свободна и образована из энергетических уровней внеш­них «коллективизированных» электронов изолированных атомов.

В зависимости от степени заполнения зон электронами и ширины запрещенной зоны возможны четыре случая, изображенные на рис. 314. На рис. 314, а самая верхняя зона, содержащая электроны, заполнена лишь частично, т. е. в ней имеются вакантные уровни. В данном случае электрон, получив сколь угодно малую энергетическую «добавку» (например, за счет теплового движения или электрического поля), сможет перейти на более высокий энергетический уровень той же зоны, т. е. стать свободным и участвовать в проводимости. Внутризонный переход вполне возможен, так как, например, при 1 К энергия теплового движения kT»10^–4 эВ, т. е. гораздо больше разности энергий между соседними уровнями зоны (примерно 10^–22 эВ). Таким об­разом, если в твердом теле имеется зона, лишь частично заполненная электронами, то это тело всегда будет проводником электрического тока. Именно это свойственно металлам.

Твердое тело является проводником электрического тока и в том случае, когда валентная зона перекрывается свободной зоной, что в конечном счете приводит к не полностью заполненной зоне (рис. 314, б). Это имеет место для щелочноземельных элементов, образующих II группу таблицы Менделеева (Be, Mg, Ca, Zn, ...). В данном случае образуется так называемая «гибридная» зона, которая заполняется валентными электронами лишь частично. Следовательно, в данном случае металлические свойства щелочноземельных элементов обусловлены перекрытием валентной и свободной зон.

Помимо рассмотренного выше перекрытия зон возможно также перераспределение электронов между зонами, возникающими из уровней различных атомов, которое может привести к тому, что вместо двух частично заполненных зон в кристалле окажутся одна полностью заполненная (валентная) зона и одна свободная зона (зона проводимости). Твердые тела, у которых энергетический спектр электронных состоя­ний состоит только из валентной зоны и зоны проводимости, являются диэлектриками или полупроводниками в зависимости от ширины запрещенной зоны DЕ.

Если ширина запрещенной зоны кристалла порядка нескольких электрон-вольт, то тепловое движение не может перебросить электроны из валентной зоны в зону прово­димости и кристалл является диэлектриком, оставаясь им при всех реальных тем­пературах (рис. 314, в). Если запрещенная зона достаточно узка (DЕ порядка 1 эВ), то переброс электронов из валентной зоны в зону проводимости может быть осуществлен сравнительно легко либо путем теплового возбуждения, либо за счет внешнего источ­ника, способного передать электронам энергию DЕ, и кристалл является полупровод­ником (рис. 314, г).

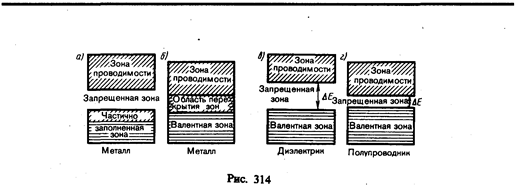
Различие между металлами и диэлектриками с точки зрения зонной теории состоит в том, что при 0 К в зоне проводимости металлов имеются электроны, а в зоне проводимости диэлектриков они отсутствуют. Различие же между диэлектриками и полупроводниками определяется шириной запрещенных зон: для диэлектриков она довольно широка (например, для NaCl DЕ=6 эВ), для полупроводников — достаточ­но узка (например, для германия DЕ=0,72 эВ). При температурах, близких к 0 К, полупроводники ведут себя как диэлектрики, так как переброса электронов в зону проводимости не происходит. С повышением температуры у полупроводников растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости, т. е. электрическая проводимость проводников в этом случае увеличи­вается.

§ 242. Собственная проводимость полупроводников

Полупроводниками являются твердые тела, которые при Т=0 характеризуются полно­стью занятой электронами валентной зоной, отделенной от зоны проводимости срав­нительно узкой (DЕ порядка 1 эВ) запрещенной зоной (рис. 314, г). Своим названием они обязаны тому, что их электропроводность меньше электропроводности металлов и больше электропроводности диэлектриков.

В природе полупроводники существуют в виде элементов (элементы IV, V и VI групп Периодической системы элементов Менделеева), например Si, Ge, As, Se, Те, и химических соединений, например оксиды, сульфиды, селениды, сплавы элементов различных групп. Различают собственные и примесные полупроводники. Собственными полупроводниками являются химически чистые полупроводники, а их проводимость называется собственной проводимостью. Примером собственных полупроводников мо­гут служить химически чистые Ge, Se, а также многие химические соединения: InSb, GaAs, CdS и др.

При 0 К и отсутствии других внешних факторов собственные полупроводники ведут себя как диэлектрики. При повышении же температуры электроны с верхних уровней валентной зоны I могут быть переброшены на нижние уровни зоны проводи­мости II (рис. 315). При наложении на кристалл электрического поля они перемещают­ся против поля и создают электрический ток. Таким образом, зона II из-за ее частичного «укомплектования» электронами становится зоной проводимости. Прово­димость собственных полупроводников, обусловленная электронами, называется элек­тронной проводимостью или проводимостью n-типа (от лат. negative — отрицательный).

В результате тепловых забросов электронов из зоны I в зону II в валентной зоне возникают вакантные состояния, получившие названиедырок. Во внешнем электричес­ком поле на освободившееся от электрона место — дырку — может переместиться электрон с соседнего уровня, а дырка появится в том месте, откуда ушел электрон, и т. д. Такой процесс заполнения дырок электронами равносилен перемещению дырки в направлении, противоположном движению электрона, так, как если бы дырка об­ладала положительным зарядом, равным по величине заряду электрона. Проводи­мость собственных полупроводников, обусловленная квазичастицами — дырками, на­зываетсядырочной проводимостью илипроводимостью p-типа (от лат. positive — поло­жительный).

Таким образом, в собственных полупроводниках наблюдаются два механизма проводимости: электронный и дырочный. Число электронов в зоне проводимости равно числу дырок в валентной зоне, так как последние соответствуют электронам, возбужденным в зону проводимости. Следовательно, если концентрации электронов проводимости и дырок обозначить соответственно п_e, и n_р, то

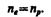(242.1)

Проводимость полупроводников всегда являетсявозбужденной, т. е. появляется только под действием внешних факторов (температуры, облучения, сильных электрических полей и т. д.).

В собственном полупроводнике уровень Ферми находится в середине запрещенной зоны (рис. 316). Действительно, для переброса электрона с верхнего уровня валентной зоны на нижний уровень зоны проводимости затрачиваетсяэнергия активации, равная ширине запрещенной зоны DE. При появлении же электрона в зоне проводимости в валентной зоне обязательно возникает дырка. Следовательно, энергия, затраченная на образование пары носителей тока, должна делиться на две равные части. Так как энергия, соответствующая половине ширины запрещенной зоны, идет на переброс электрона и такая же энергия затрачивается на образование дырки, то начало отсчета для каждого из этих процессов должно находиться в середине запрещенной зоны. Энергия Ферми в собственном полупроводнике представляет собой энергию, от кото­рой происходит возбуждение электронов и дырок.

Вывод о расположении уровня Ферми в середине запрещенной зоны собственного полупро­водника может быть подтвержден математическими выкладками. В физике твердого тела до­казывается, что концентрация электронов в зоне проводимости

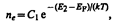(242.2)

где E₂—энергия, соответствующая дну зоны проводимости (рис. 316), Е_F — энергия Ферми, Т — термодинамическая температура, С₁ — постоянная, зависящая от температуры и эффектив­ной массы электрона проводимости.Эффективная масса — величина, имеющая размерность массы и характеризующая динамические свойства квазичастиц — электронов проводимости и ды­рок. Введение в зонную теорию эффективной массы электрона проводимости позволяет, с одной стороны, учитывать действие на электроны проводимости не только внешнего поля, но и внутрен­него периодического поля кристалла, а с другой стороны, абстрагируясь от взаимодействия электронов проводимости с решеткой, рассматривать их движение во внешнем поле как движение свободных частиц.

Концентрация дырок в валентной зоне

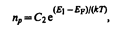(242.3)

где С₂ — постоянная, зависящая от температуры и эффективной массы дырки, Е₁ — энергия, соответствующая верхней границе валентной зоны. Энергия возбуждения в данном случае от­считывается вниз от уровня Ферми (рис. 316), поэтому величины в экспоненциальном множителе (242.3) имеют знак, обратный знаку экспоненциального множителя в (242.2). Так как для собствен­ного полупроводника п_e=n_p (242.1), то

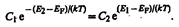
Если эффективные массы электронов и дырок равны ( 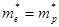), то С₁=С₂ и, следовательно, –(E₂–E_F)= =E₁–E_F, откуда

т. е. уровень Ферми в собственном полупроводнике действительно расположен в середине запре­щенной зоны.

Taк как для собственных полупроводников DE>>kT, то распределение Фер­ми — Дирака (235.2) переходит в распределение Максвелла — Больцмана. Положив в (236.2) E–E_F » DE/2, получим

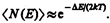(242.4)

Количество электронов, переброшенных в зону проводимости, а следовательно, и ко­личество образовавшихся дырок пропорциональны áN(Е)ñ. Таким образом, удельная проводимость собственных полупроводников

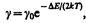(242.5)

где g₀ — постоянная, характерная для данного полупроводника.

Увеличение проводимости полупроводников с повышением температуры является их характерной особенностью (у металлов с повышением температуры проводимость уменьшается). С точки зрения зонной теории это обстоятельство объяснить довольно просто: с повышением температуры растет число электронов, которые вследствие теплового возбуждения переходят в зону проводимости и участвуют в проводимости. Поэтому удельная проводимость собственных полупроводников с повышением тем­пературы растет.

Если представить зависимость ln g от 1/T, то для собственных полупроводни­ков — это прямая (рис. 317), по наклону которой можно определить ширину запрещен­ной зоны DЕ, а по ее продолжению — g₀ (прямая отсекает на оси ординат отрезок, равный ln g₀).

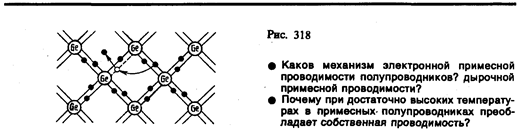
Одним из наиболее широко распространенных полупроводниковых элементов явля­ется германий, имеющий решетку типа алмаза, в которой каждый атом связан ковалентными связями (см. § 71) с четырьмя ближайшими соседями. Упрощенная плоская схема расположения атомов в кристалле Ge дана на рис. 318, где каждая черточка обозначает связь, осуществляемую одним электроном. В идеальном кристалле при 0 К такая структура представляет собой диэлектрик, так как все валентные электроны участвуют в образовании связей и, следовательно, не участвуют в проводимости.

При повышении температуры (или под действием других внешних факторов) тепловые колебания решетки могут привести к разрыву некоторых валентных связей, в результате чего часть электронов отщепляется и они становятся свободными. В поки­нутом электроном месте возникает дырка (она изображена белым кружком), заполнить которую могут электроны из соседней пары. В результате дырка, так же как и освобо­дившийся электрон, будет двигаться по кристаллу. Движение электронов проводимо­сти и дырок в отсутствие электрического поля является хаотическим. Если же на кристалл наложить электрическое поле, то электроны начнут двигаться против поля, дырки— по полю, что приведет к возникновению собственной проводимости герма­ния, обусловленной как электронами, так и дырками.

В полупроводниках наряду с процессом генерации электронов и дырок идет процесс рекомбинации: электроны переходят из зоны проводимости в валентную зону, отдавая энергию решетке и испуская кванты электромагнитного излучения. В результате для каждой температуры устанавливается определенная равновесная концентрация элект­ронов и дырок, изменяющаяся с температурой согласно выражению (242.4).

§ 243. Примесная проводимость полупроводников

Проводимость полупроводников, обусловленная примесями, называетсяпримесной проводимостью, а сами полупроводники —примесными полупроводниками. Примесная проводимость обусловлена примесями (атомы посторонних элементов), а также дефек­тами типа избыточных атомов (по сравнению со стехиометрическим составом), тепло­выми (пустые узлы или атомы в междоузлиях) и механическими (трещины, дислокации и т. д.) дефектами. Наличие в полупроводнике примеси существенно изменяет его проводимость. Например, при введении в кремний примерно 0,001 ат.% бора его проводимость увеличивается примерно в 10⁶ раз.

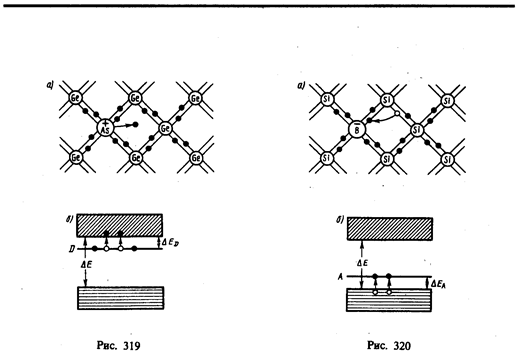
Примесную проводимость полупроводников рассмотрим на примере Ge и Si, в которые вводятся атомы с валентностью, отличной от валентности основных атомов на единицу. Например, при замещении атома германия пятивалентным атомом мы­шьяка (рис. 319, а) один электрон не может образовать ковалентной связи, он оказыва­ется лишним и может быть легко при тепловых колебаниях решетки отщеплен от атома, т. е. стать свободным. Образование свободного электрона не сопровождается нарушением ковалентной связи; следовательно, в отличие от случая, рассмотренного в § 242, дырка не возникает. Избыточный положительный заряд, возникающий вблизи атома примеси, связан с атомом примеси и поэтому перемещаться по решетке не может.

С точки зрения зонной теории рассмотренный процесс можно представить следу­ющим образом (рис. 319, б). Введение примеси искажает поле решетки, что приводит к возникновению в запрещенной зоне энергетического уровня D валентных электронов мышьяка, называемогопримесным уровнем. В случае германия с примесью мышьяка этот уровень располагается от дна зоны проводимости на расстоянии DE_D=0,013 эВ. Так как DE_D<kT, то уже при обычных температурах энергия теплового движения достаточна для того, чтобы перебросить электроны примесного уровня в зону проводимости; образующиеся при этом положительные заряды локализуются на неподвижных атомах мышьяка и в проводимости не участвуют.

Таким образом, в полупроводниках с примесью, валентность которой на единицу больше валентности основных атомов, носителями тока являются электроны; воз­никает электронная примесная проводимость (проводимость n-типа). Полупроводники с такой проводимостью называются электронными (или полупроводниками n-типа). Примеси, являющиеся источником электронов, называются донорами, а энергетические уровни этих примесей — донорными уровнями.

Предположим, что в решетку кремния введен примесный атом с тремя валентными электронами, например бор (рис. 320, а). Для образования связей с четырьмя ближай­шими соседями у атома бора не хватает одного электрона, одна из связей остается неукомплектованной и четвертый электрон может быть захвачен от соседнего атома основного вещества, где соответственно образуется дырка. Последовательное заполне­ние образующихся дырок электронами эквивалентно движению дырок в полупровод­нике, т. е. дырки не остаются локализованными, а перемещаются в решетке кремния как свободные положительные заряды. Избыточный же отрицательный заряд, воз­никающий вблизи атома примеси, связан с атомом примеси и по решетке перемещать­ся не может.

По зонной теории, введение трехвалентной примеси в решетку кремния приводит к возникновению в запрещенной зоне примесного энергетического уровня А, не занято­го электронами. В случае кремния с примесью бора этот уровень располагается выше верхнего края валентной зоны на расстоянии DE_A=0,08 эВ (рис. 320, б). Близость этих уровней к валентной зоне приводит к тому, что уже при сравнительно низких тем­пературах электроны из валентной зоны переходят на примесные уровни и, связываясь с атомами бора, теряют способность перемещаться по решетке кремния, т. е. в прово­димости не участвуют. Носителями тока являются лишь дырки, возникающие в ва­лентной зоне.

Таким образом, в полупроводниках с примесью, валентность которой на единицу меньше валентности основных атомов, носителями тока являются дырки; возникает дырочная проводимость (проворность p-типа). Полупроводники с такой проводимостью называются дырочными (или полупроводниками p-типа). Примеси, захватывающие электроны из валентной зоны полупроводника, называются акцепторами, а энергети­ческие уровни этих примесей — акцепторными уровнями.

В отличие от собственной проводимости, осуществляющейся одновременно элект­ронами и дырками, примесная проводимость полупроводников обусловлена в основ­ном носителями одного знака: электронами—в случае донорной примеси, дырка­ми — в случае акцепторной. Эти носители тока называются основными. Кроме основ­ных носителей в полупроводнике имеются и неосновные носители: в полупроводниках n-типа — дырки, в полупроводниках p-типа — электроны.

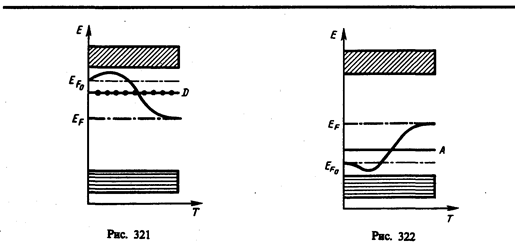
Наличие примесных уровней в полупроводниках существенно изменяет положение уровня Ферми Е_F. Расчеты показывают, что в случае полупроводников n-типа уровень Ферми Е_F0 при 0 К расположен посередине между дном зоны проводимости и донорным уровнем (рис. 321), С повышением температуры все большее число электронов переходит из донорных состояний в зону проводимости, но, помимо этого, возрастает и число тепловых флуктуаций, способных возбуждать электроны из валентной зоны и перебрасывать их через запрещенную зону энергий. Поэтому при высоких тем­пературах уровень Ферми имеет тенденцию смещаться вниз (сплошная кривая) к свое­му предельному положению в центре запрещенной зоны, характерному для собствен­ного полупроводника.

Уровень Ферми в полупроводниках р-типа при 0 К Е_F0 располагается посередине между потолком валентной зоны и акцепторным уровнем (рис. 322). Сплошная кривая опять-таки показывает его смещение с температурой. При температурах, при которых примесные атомы оказываются полностью истощенными и увеличение концентрации носителей происходит за счет возбуждения собственных носителей, уровень Ферми располагается посередине запрещенной зоны, как в собственном полупроводнике.

Проводимость примесного полупроводника, как и проводимость любого провод­ника, определяется концентрацией носителей и их подвижностью. С изменением тем­пературы подвижность носителей меняется по сравнительно слабому степенному зако­ну, а концентрация носителей — по очень сильному экспоненциальному закону, поэто­му проводимость примесных полупроводников от температуры определяется в основ­ном температурной зависимостью концентрации носителей тока в нем. На рис. 323 дан примерный график зависимости ln g от 1/T для примесных полупроводников. Участок AB описывает примесную проводимость полупроводника. Рост примесной проводимо­сти полупроводника с повышением температуры обусловлен в основном ростом концентрации примесных носителей. Участок ВС соответствует области истощения примесей (это подтверждают и эксперименты), участок CD описывает собственную проводимость полупроводника.

§ 244. Фотопроводимость полупроводников

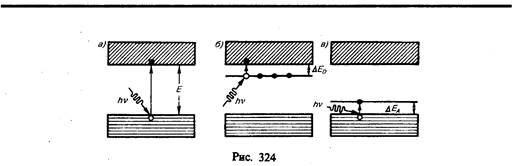
Фотопроводимость (см. § 202)полупроводников — увеличение электропроводности полу­проводников под действием электромагнитного излучения — может быть связана со свойствами как основного вещества, так и содержащихся в нем примесей. В первом случае при поглощении фотонов, соответствующих собственной полосе поглощения полупроводника, т. е. когда энергия фотонов равна или больше ширины запрещенной зоны (hn ³ DE), могут совершаться перебросы электронов из валентной зоны в зону проводимости (рис. 324, а), что приведет к появлению добавочных (неравновесных) электронов (в зоне проводимости) и дырок (в валентной зоне). В результате возникает собственная фотопроводимость, обусловленная как электронами, так и дырками.

Если полупроводник содержит примеси, то фотопроводимость может возникать и при hn < DE: для полупроводников с донорной примесью фотон должен обладать энергией hn ³ DЕ_D, а для полупроводников с акцепторной примесью — hn ³ DЕ_A. При поглощении света примесными центрами происходит переход электронов с донорных уровней в зону проводимости в случае полупроводника n-типа (рис. 324, б) или из валентной зоны на акцепторные уровни в случае полупроводника p-типа (рис. 324, в). В результате возникаетпримесная фотопроводимость, являющаяся чисто электронной для полупроводников п-типа и чисто дырочной для полупроводников p-типа.

Таким образом, если

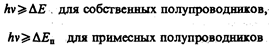(244.1)

(DE_п — в общем случае энергия активации примесных атомов), то в полупроводнике возбуждается фотопроводимость. Из (244.1) можноопределитькрасную границу фотопроводимости — максимальную длину волны, при которой еще фотопроводимость возбуждается:

Учитывая значения DE и DE_п для конкретных полупроводников, можно показать, что красная граница фотопроводимости для собственных полупроводников приходится на видимую область спектра, для примесных же полупроводников — на инфрак­расную.

На рис. 325 представлена типичная зависимость фотопроводимости j и коэффициен­та поглощения { от длины волны l падающего на полупроводник света. Из рисунка следует, что при l>l₀ фотопроводимость действительно не возбуждается. Спад фото­проводимости в коротковолновой части полосы поглощения объясняется большой скоростью рекомбинации в условиях сильного поглощения в тонком поверхностном слое толщиной х»1 мкм (коэффициент поглощения »10⁶ м^–1).

Наряду с поглощением, приводящим к появлению фотопроводимости, может иметь место экситонный механизм поглощения. Экситоны представляют собой квази­частицы — электрически нейтральные связанные состояния электрона и дырки, образу­ющиеся в случае возбуждения с энергией, меньшей ширины запрещенной зоны. Уровни энергии экситонов располагаются у дна зоны проводимости. Так как экситоны элект­рически нейтральны, то их возникновение в полупроводнике не приводит к появлению дополнительных носителей тока, вследствие чего экситонное поглощение света не сопровождается увеличением фотопроводимости.

§ 245. Люминесценция твердых тел

В природе давно известно излучение, отличное по своему характеру от всех известных видов излучения (теплового излучения, отражения, рассеяния света и т. д.). Этим излучением является люминесцентное излучение, примерами которого может служить свечение тел при облучении их видимым, ультрафиолетовым и рентгеновским излуче­нием, g-излучением и т.д. Вещества, способные под действием различного рода возбуждений светиться, получили названиелюминофоров.

Люминесценция — неравновесное излучение, избыточное при данной температуре над тепловым излучением тела и имеющее длительность, большую периода световых колебаний. Первая часть этого определения приводит к выводу, что люминесценция не является тепловым излучением (см. § 197), поскольку любое тело при температуре выше 0 К излучает электромагнитные волны, а такое излучение является тепловым. Вторая часть показывает, что люминесценция не является таким видом свечения, как отражение и рассеяние света, тормозное излучение заряженных частиц и т. д. Период световых колебаний составляет примерно 10^–15 с, поэтому длительность, по которой свечение можно отнести к люминесценции, больше—примерно 10^–10 с. Признак длительности свечения дает возможность отличить люминесценцию от других нерав­новесных процессов. Так, по этому признаку удалось установить, что излучение Вавилова — Черенкова (см. § 189) нельзя отнести к люминесценции.

В зависимости от способов возбуждения различают:фотолюминесценцию (под действием света),рентгенолюминесценцию (под действием рентгеновского излучения), катодолюминесценцию (под действием электронов),электролюминесценцию (под дейст­вием электрического поля),радиолюминесценцию (при возбуждении ядерным излучени­ем, например g-излучением, нейтронами, протонами),хемилюминесценцию (при хи­мических превращениях),триболюминесценцию (при растирании и раскалывании неко­торых кристаллов, например сахара). По длительности свечения условно различают: флуоресценцию(t£10^–8с)ифосфоресценцию —свечение, продолжающееся заметный промежуток времени после прекращения возбуждения.

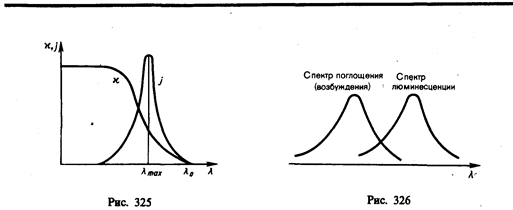
Первое количественное исследование люминесценции проведено более ста лет назад Дж. Стоксом,* сформулировавшим в 1852 г. следующее правило: длина вол­ны люминесцентного излучения всегда больше длины волны света, возбудившего его (рис. 326). Согласно квантовой теории, правило Стокса означает, что энергия hn падающего фотона частично расходуется на какие-то неоптические процессы, т. е.

откуда n_люм<n или l_люм>l что и следует из сформулированного правила.

* Дж. Стокс (1819—1903) — английский физик и математик.

Основной энергетической характеристикой люминесценции являетсяэнергетический выход, введенный С. И. Вавиловым в 1924 г., — отношение энергии, излученной люминофором при полном высвечивании, к энергии, поглощенной им. Типичная для органических люминофоров (на примере раствора флуоресцина) зависимость энергетического выхода h от длины волны l возбуждающего света представлена на рис. 327. Из рисунка следует, что вначале h растет пропорционально l, а затем, достигая максимального значения, быстро спадает до нуля при дальнейшем уве­личении l (закон Вавилова). Величина энергетического выхода для различных лю­минофоров колеблется в довольно широких пределах, максимальное ее значение может достигать примерно 80%.