Стохастическое моделирование факторных систем.

Если зависимость между факторами и результативным показателем не удается описать ни одним их приведенных выше видов детерминированных факторных систем, то аналитические процедуры переходят в область стохастического анализа, который направлен на изучение косвенных связей, то есть влияние факторов на результативный показатель является опосредованным. Стохастический анализ является углублением детерминированного факторного анализа. Исходным условием реализации задач стохастического анализа является возможность повторного измерения параметров одного и того же экономического процесса в различных условиях. Модель составляется на основе совокупности эмпирических данных. Другими условиями стохастического моделирования являются качественная однородность данных, достаточная размерность (численность) совокупности наблюдений, а также наличие методов, позволяющих выявить достоверные количественные параметры связей экономических показателей и факторов. В исследовании стохастических факторных систем используется такой математический аппарат, как оценка связи и корреляции между показателями и факторами, регрессионный анализ, выявление параметров периодических колебаний показателей, группировка многомерных наблюдений, дисперсионный анализ и т.д.

Наиболее распространенной задачей стохастического анализа является изучение наличия, направления и интенсивности связей между показателями. Предположение о наличии и тесноте связи делается в случае выявления общих закономерностей в изменении значений показателей. Исследование связи производится с помощью корреляционного анализа. В зависимости от поставленной задачи и характера исходной информации рассчитывается коэффициент корреляции (или корреляционное отношение) по формуле:

,

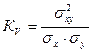где ; = ^; = ,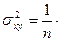

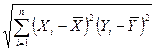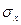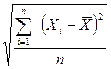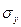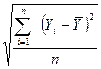X_i – i -ое значение фактора;

Y_i - i –ое значение результативного показателя;

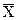- среднеарифметическое значение фактора;

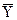- среднеарифметическое значение результативного показателя.

n – количество наблюдений.

Полученные значения коэффициентов сравниваются с значениями корреляционной шкалы для установления факта наличия связи между показателями или ее отсутствия. Считается, что при значении коэффициента корреляции менее 0,5 связь отсутствует. Если значение коэффициента корреляции более 0,5, то связь между показателями существует, причем, чем ближе коэффициент корреляции к единице, тем связь более тесная. Если коэффициент корреляции достаточно близок к единице, то характер зависимости между фактором (х) и результативным показателем (у) можно описать уравнением прямой у = а + в х , где коэффициент в рассматривается как коэффициент регресии, определяющий интенсивность связи между фактором и результативным показателем. Уравнение решается относительно коэффициентов а и в способом наименьших квадратов. Коэффициент в показывает, на какую величину изменяется результативный показатель (у) при изменении фактора (х) на единицу.

Для обработки больших объемов цифровой информации созданы и успешно функционируют компьютерные программные продукты, выполняющие в том числе и расчетно-аналитические операции. С помощью таких программ реализуются различные методики финансового и управленческого анализа, финансового планирования, бюджетирования, контроллинга и т.д. Компьютерные аналитические программы функционируют самостоятельно, а также в составе системного компьютерного обеспечения. Одновременное использование правовых консультационных программ расширяет аналитические возможности программных продуктов, позволяет применять их в различных отраслях, на предприятиях различных организационно-правовых форм и масштабов деятельности. К числу таких программных комплексов относятся «Турбо Бухгалтер», «ИНЕК», «1С», «АФСП», «Парус», «Инотек» и др.