Детерминированное моделирование факторных систем.
Моделирование – один из важнейших методов научного познания, с помощью которого создается модель (условный образ) объекта исследования. Экономико-математическое моделирование широко применяется в экономическом анализе для изучения экономических процессов и явлений, оценки показателей хозяйственной деятельности. Сущность этого метода заключается в том, что взаимосвязь исследуемого показателя с факторами передается в виде конкретного математического уравнения (неравенства). Экономико-математическая модель должна быть адекватна действительности, отражать существенные стороны и связи изучаемого объекта. Процесс моделирования условно подразделяется на четыре этапа:
¨ установление теоретических закономерностей, присущих анализируемому экономическому процессу;
¨ анализ эмпирических данных, отражающих структуру, динамику показателей;
¨ выбор методов решения задачи;
¨ анализ полученных результатов.
В процессе создания экономико-математической модели часто возникает проблема, связанная со сложностью формализации экономического процесса (включения в модель всех элементов, факторов). Возникает необходимость упрощения модели, исключения второстепенных характеристик. Так, одной из наиболее сложных задач экономико-математического моделирования является построение модели экономики предприятия в целом. Экономико-математическая модель конкретного показателя хозяйственной деятельности представляет собой факторную систему. Факторы, как элементы модели, должны обладать причинностью, достаточной специфичностью, самостоятельностью существования, возможностью количественного измерения, учетной возможностью.
В экономическом анализе исследуются факторные модели, отражающие функциональные зависимости между результативным показателем и факторами, включенными в модель. Моделирование таких факторных систем называется детерминированным моделированием. Широкую известность имеет разработанная специалистами компании «Дюпон» (Du Pont model) система моделирования исходной кратной факторной модели рентабельности активов, которая позволяет описать взаимосвязь обобщающего показателя эффективности бизнеса (рентабельности) с воздействующими на него факторами рентабельности продаж и оборачиваемости активов.
Детерминированные факторные системы можно моделировать, используя следующие основные приемы.
1. Метод удлинения факторной системы.
Исходная факторная система: 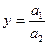 . Если а1 представить в виде суммы отдельных слагаемых-факторов: a1 = а 1,1 + а 1,2 + а 1,3 + … + а i, n, то:
. Если а1 представить в виде суммы отдельных слагаемых-факторов: a1 = а 1,1 + а 1,2 + а 1,3 + … + а i, n, то:
y= 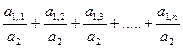 - конечная факторная система вида y =
- конечная факторная система вида y = 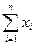 .
.
2. Метод расширения факторной системы.
Исходная факторная система: 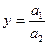 . Если и числитель, и знаменатель умножить на одно и то же число (расширить), то получим новую факторную систему:
. Если и числитель, и знаменатель умножить на одно и то же число (расширить), то получим новую факторную систему:
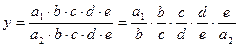 , то есть мультипликативную модель вида:
, то есть мультипликативную модель вида:
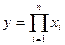
3. Метод сокращения факторной системы.
Исходная факторная система: 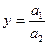 . Если и числитель, и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему:
. Если и числитель, и знаменатель дроби разделить на одно и то же число, то получим новую факторную систему:
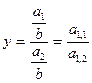 . Конечная факторная система имеет вид:
. Конечная факторная система имеет вид: 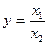 .
.
Каждый показатель доходности или рентабельности представляет собой двухфакторную модель 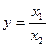 , которая путем моделирования преобразуется в многофакторные аддитивные, кратные или мультипликативные.
, которая путем моделирования преобразуется в многофакторные аддитивные, кратные или мультипликативные.
Пример 1: 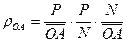 =
= 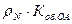 или
или 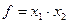 (мультипликативная двухфакторная модель). Влияние факторов рассчитывается методом абсолютных разниц:
(мультипликативная двухфакторная модель). Влияние факторов рассчитывается методом абсолютных разниц:
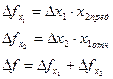
Пример 2:мультипликативная пятифакторная модель:
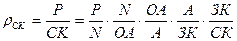 или
или 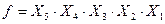
Путем моделирования исходной кратной двухфакторной модели рентабельности собственного капитала можно получить четырехфакторную мультипликативную модель:
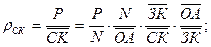 или
или 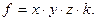
Дата добавления: 2017-04-20; просмотров: 955;
