Постановка задачи регрессии

Поставим задачу регрессии Y на X.

Пусть мы располагаем n парами выборочных наблюдений над двумя переменными X и Y:

Функция f(X) называется функцией регрессии Y по X, если она описывает изменение условного среднего значения результирующей переменной Y в зависимости от изменения значений объясняющей переменной X: f(X)=E(Y |X).

Таким образом, имеет место уравнение регрессионной связи между Y и X:

Y_i =f(X_i)+u_i, i=1,…,n. (2.2)

Присутствие в модели (2.2) случайной "остаточной" компоненты u, также называемой случайным членом, обусловлено следующими причинами:

1. Ошибки спецификации. Среди них выделяют невключение важных объясняющих переменных, агрегирование (объединение) переменных, неправильную функциональную спецификацию модели.

2. Ошибки измерения. Связаны со сложностью сбора исходных данных и использованием в модели аппроксимирующих переменных для учета факторов, непосредственное измерение которых невозможно.

3. Ошибки, связанные со случайностью человеческих реакций. Обусловлены тем, что поведение и непосредственное участие человека в ходе сбора и подготовки данных может быть достаточно непредсказуемым и вносит, таким образом, свой вклад в случайный член.

Мы хотим на основе выборочных наблюдений с учетом дополнительных требований, налагаемых на u, статистически оценить функцию f(X), проверить оптимальность полученной оценки и использовать уравнение для построения прогноза.

Допущения модели. Относительно u необходимо принять ряд гипотез, известных как условия Гаусса-Маркова:

1. Eu_i=0, i=1,…,n.

Это требование состоит в том, что математическое ожидание случайного члена в любом наблюдении должно быть равно нулю. Иногда случайный член будет положительным, иногда отрицательным, но он не должен иметь систематического смещения ни в одном из двух возможных направлений. Свойство непосредственно вытекает из смысла функции регрессии. Возьмем в (2.2) матожидание от обеих частей при фиксированном значении X, получим: E(Y|X) =E(f(X))+E(u), по свойству матожидания Þ E(Y|X) =f(X)+E(u), а поскольку с учетом определения функции регрессии должно быть f(X)=E(Y |X), то необходимо E(u)=0.

2.

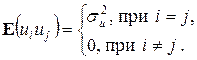
Первая строчка означает требование постоянства дисперсии регрессионных остатков (независимость от того, при каких значениях объясняющей переменной производятся наблюдения i), которое называют гомоскедастичностью остатков. Вторая строчка предполагает отсутствие систематической связи между значениями случайного члена в любых двух наблюдениях, которые должны быть абсолютно независимы друг от друга.

3. X₁, …, X_n – неслучайные величины.

Таким образом, задача регрессии имеет вид:

Y_i =f(X_i)+u_i, i=1,…,n.

а. Eu_i=0, i=1,…,n. (2.3)

б. 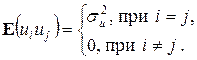(2.4)

в. X₁, …, X_n – неслучайные величины. (2.5)

При выборе вида функции f в (2.2) обычно руководствуются следующими рекомендациями:

§ используется априорная информация о содержательной экономической сущности анализируемой зависимости – аналитический способ,

§ предварительный анализ зависимости с помощью визуализации – графический способ,

§ использование различных статистических приемов обработки исходных данных и экспериментальных расчетов.