Задачи изучения темы.

Методика обучения математике в дочисловой период.

На уроках дочислового периода надо систематизировать и пополнять знания, умения и навыки, которыми обладают дети, дать те знания, которые необходимы для изучения нумерации.

Задачи изучения темы.

1. Должно быть отработано умение вести счет различных объектов (предметов, звуков, движений). Дети должны усвоить, что, отвечая на вопрос «сколько?», предметы можно считать в любом порядке, а на вопрос «который по счету?» - в определенном, указанном порядке.

На уроках дочислового периода дети считают хором, по цепочке, индивидуально, по представлению (Сколько этажей в школе? Сколько героев в сказке «Репка»?)

Дети знакомятся с аксиомой счета - считать можно в любом порядке (слева направо, справа налево, вразброс, соблюдая при этом следующие требования:

- не пропускать при счете ни один предмет;

- ни один предмет не считать дважды.

2. На основе многочисленных практических упражнений дети должны научиться сравнивать две группы предметов, выясняя, в которой из них содержится больше (меньше) предметов, или же убедиться в том, что они содержат равное число предметов.

Сравнение ведется без счета – образованием пар предметов, а также с помощью счета предметов. Сравнение ведется в обе стороны: если в одной из сравниваемых групп предметов больше, то в другой - на столько же меньше. Решается задача по уравниванию количества предметов в группах (двумя способами: добавляют недостающие предметы, убирают «лишние»)

3. На этих уроках уточняются пространственные представления: дети должны научиться различать, например, на странице учебника верхнюю и нижнюю картинку, левую и правую страницы учебника, большой рисунок и маленький, научиться понимать выражения «выше», «ниже», «направо», «справа налево» и т.п.

4. Дети должны научиться понимать выражения, отражающие порядковые отношения: «следовать за», «стоять (идти) перед», «находиться между».

Продолжительность дочислового периода- приблизительно неделя (5-6 уроков). На первой неделе занятий дети учатся работать со счетным материалом, с книгой и в тетради. Формирование соответствующих умений и навыков на уроках дочислового периода только начинается, оно будет продолжено на уроках по теме «Нумерация».

В РОЗ дочисловой период не имеет четких границ. Уже на первых уроках появляются задания, направленные на развитие: сколько яблок в корзине – зад.5 (варианты ответов).

Самый продолжительный дочисловой период в «Школе 2000» - 17 уроков периода. Помимо основных видов деятельности, дети группируют предметы по разным признакам, в т.ч. по форме, цвету, размеру. Вводятся сложение и вычитание на множествах, переместительное свойство умножения.

Вопрос 2. Методика изучения нумерации чисел первого десятка

Нумерация – это система изучения чисел. В традиции (учебник Моро М.И.) изучению чисел предшествует подготовительный период, где дети усваивают особенности счета предметов и отношения «больше», «меньше», «столько же». Изучение чисел происходит последовательно от1, 2 до 10, затем знакомятся с числом 0. При изучении этой темы дети должны уяснить образование чисел первого десятка, обозначение их на письме, положение в натуральном ряду чисел, состав чисел и научиться выполнять сложение и вычитание вида а+1, а-1. В соответствии с этим подходом последовательно рассматриваются отрезки натурального ряда чисел 1 2, 1 2 3, 1 2 3 4 , …1 2…10. При этом упражнения выполняются однотипные:

· положите 3 квадрата;

· придвиньте еще один;

· Сколько всего стало квадратов?

· Как получили 4 квадрата?

· Как это записать? (3+1=4)

Проведя такие рассуждения 3-4 раза. Только с другими предметами. Выясняют, что число 4 больше числа 3 на 1. а число 3 меньше числа 4 на 1. Таким образом, число 4 стоит в ряду чисел после 3. Получая следующее число. Учащиеся знакомятся с соответствующей цифрой и учатся е писать. Такое одновременное введение числа и цифры затрудняет осознание различий между этими понятиями.

Число 0 появляется как численность множества, из которого последовательно убираются все элементы.

В системе РОЗ знакомство с числами построено иначе – число выступает как количественная характеристика множества. Порядок знакомства с однозначными числами не имеет значения. Учащиеся используют карточки с цифрами при счете предметов, сравнении множеств. Основой сравнения является установление взаимно однозначных соответствий между элементами двух множеств. Результаты сравнения фиксируются равенствами 5=5 или неравенствами 5<7. После знакомства со всеми однозначными числами происходит их упорядочивание, и учащиеся знакомятся с понятиями «натуральный ряд чисел», «отрезок натурального ряда».

Закрепляя принципы образования натурального ряда чисел, можно использовать «волшебные» цифры Микулиной Г.Г. Эта идея нашла свое отражение во многих альтернативных учебниках (например, Петерсон Л.Г.)

Изучение чисел в РОД предшествует длительная работа с величинами, в результате которой учащиеся овладевают общими приемами постановки и решения учебных задач, выделяя в предметах их существенные свойства, сравнивая их, они учатся отражать результаты сравнения в виде графических схем. Буквенных равенств и неравенств. Число в системе РОД является особым отношением величины А к мерке е. Рассматривая вначале только натуральные числа, учащиеся знакомятся с изображением чисел у разных народов. Числа, показывающие количество мерок в величине, изображаются на числовом луче. Принятая арабская нумерация на этом этапе рассматривается как одна из возможных. В дальнейшем она становится основной.

Вопрос 3. Методика изучения нумерации в концентре «Сотня»

Задачи изучения темы

1. Познакомить учащихся с новой счетной единицей – десятком.

2. Ввести и разъяснить понятие разряда. Усвоить, что 10 единиц составляют 1 десяток (принцип построения десятичной системы счисления)

3. Научиться считать и записывать двузначные числа.

4. Осознать различие между цифрой и числом. Понять позиционный метод записи чисел цифрами (поместное значение цифр).

5. Сформировать умение складывать и вычитать числа на основе знания нумерации двузначных чисел.

6. В тесной связи с изучением нумерации двузначных чисел рассмотреть новые единицы длины (дециметр, метр).

При изучении нумерации в концентре «Сотня» выделяются два этапа:

«Числа 11-20» и

«Числа 21-100».

Это объясняется особенностями образования числительных второго десятка, усвоение которых вызывает затруднение у большинства учащихся. Эти трудности связаны с тем, что в названии каждого числа второго десятка наблюдается одна закономерность, а в записи числа – другая. Так, называя число, мы называем сначала количество единиц, а затем – десятков, например один-на-дцать, три-на-дцать, четыр-на дцать, а записывая число, мы сначала записываем цифру 1, обозначающую десяток, а затем цифру, обозначающую единицы.

Для того, чтобы дети сознательно усвоили устную и письменную нумерацию чисел 11-20, необходимо использовать пучок палочек (десяток), и отдельные палочки. Связав 10 палочек в пучок, учитель вводит его название - «десяток», а затем, добавляя по одной палочке, знакомит учащихся с названиями чисел в натуральном ряду, каждый раз обращая внимание учащихся на структуру числительного.

При изучении нумерации двузначных чисел у учащихся формируются первые представления о десятичной позиционной системе счисления. Усваивая названия и запись чисел от 11 до 20, они используют термины «Единицы», «Десятки» и правила «Единицы пишутся на первом месте справа, десятки на втором». Для того, чтобы введение новых терминов не было формальным, следует уделить особое внимание разъяснению принципов образования названий двузначных чисел и их записи. Для этой цели используются те понятия, которые рассматривались ими при изучении чисел от 1 до 10. На практике это может выглядеть так:

а) учащимся предлагается совокупность предметов. Определяя их количество с помощью счета, они получают число 10;

б) к совокупности добавляется еще один предмет;

в) это изменение фиксируется в записи 10+1;

г) возникает задача – как назвать число, следующее за число 10?

Небольшой экскурс учителя в историю названия числа 10 («дцать») и словесное фиксирование выполняемых действий «один прибавили к дцать» - один на дцать позволяет учащимся высказать догадку о названии нового числа. Затем добавляется ещё один предмет, теперь к 10 прибавили 2 (10+2 «два прибавили к дцать» - два-на-дцать - две на дцать) и т.д. Осознание закономерности способствует формированию общего способа действия. В практике работы, особенно с семилетними детьми учителю, конечно, вряд ли придется столкнуться с такой ситуацией, когда они не назовут или не запишут числа, следующего за числом 10. В этом случае приведенное выше разъяснение следует использовать, для того, чтобы ответить на вопрос – «Почему число, следующее за числом десять, имеет такое название?». Чтобы ребенок осознал принцип записи двузначных чисел, необходимо, прежде всего, акцентировать его внимание на записи цифры 1 единицы, и 1 десятка. Для этой цели можно соотнести число 1 с одной палочкой, число 10 «один десяток» – с десятью палочками, связанными в пучок. Связывая десять палочек в пучок, ученики практически убеждаются в том, что не осталось ни одной палочки, помимо тех, которые связаны в пучок. Отсюда у них возникает представление о единицах и десятках, и они быстро усваивают закономерность в записи двузначных чисел. Для осознания принципа записи двузначных чисел полезно также выяснить сходства и различия в записи чисел 10 и 11, 10 и 12, 11 и 12, 12 и 13 и т.д.

В теме «Нумерация» рассматриваются случаи сложения и вычитания чисел, основой вычисления в которых служит разрядный состав число и принцип образования чисел в натуральном ряду (например, такие: 18-8, 18-10, 10+8, 14+1, 17-1).

В учебниках И.И.Аргинской нумерация чисел изучается не по концентрам, по разделам «однозначные числа», «двузначные числа» и т.д. Среди двузначных чисел выделяется последовательно отрезки натурального ряда 10-19, 20-29, …, 90-99, в которых рассматриваются те же вопросы, что и в традиционной системе.

В системе РОД для записи чисел выбирается система мерок е ₁, е ₂, е ₃…, с помощью которой можно записать любое число (сначала двузначное, потом многозначное). Отношение между мерками может быть любым, поэтому числа можно записывать в любой системе счисления.

Например, отношение е ₂ / е ₁ = 5, т.е. в мерке е ₂ содержится 5 мерок е ₁. Если в величине А мерка е ₂ укладывается 4 раза и еще 2 раза мерка е ₁ е ₂, то значение величины А записывается в пятеричной системе так: 42₅. Если отношение мерок равно 10, то такая система счисления называется десятичной.

Учащиеся при таком подходе усваивают общий принцип записи чисел и уже к концу первого класса умеют оперировать с многоразрядными числами.

Вопрос 4. Изучение нумерации трехзначных и многозначных чисел

Особенности десятичной системы счисления позволяют младшим школьникам осуществить перенос умения читать и записывать двузначные числа на область трехзначных. Появление нового разряда сотен связывается с введением новой счетной единицы (сотни). Для усвоения учащимися ее значения используются те же приемы, которые имели место при разъяснении понятия «десяток», то есть десять палочек связываются в пучок и получается десяток. Если же десять таких пучков объединить вместе, то получим сотню «100». Усвоив, что сотни пишутся на третьем месте слева, учащиеся сначала учатся называть круглые сотни (100, 200, 300). Затем, ориентируясь на названия разрядов (единицы, десятки, сотни), овладевают умением читать и записывать любое трехзначное число. При изучении многозначных чисел вводится понятие «класс». Усвоение соотношения понятий «класс» и «разряд» представляет для младших школьников определенную трудность. С одной стороны, это обусловлено терминологией: класс единиц содержит единицы, десятки, сотни и класс тысяч также содержит единицы, десятки, сотни, но это уже единицы тысяч, десятки тысяч и сотни тысяч. С другой стороны, это обусловлено абстрактностью данных понятий и невозможностью использовать для их усвоения предметные действия. Их в этом случае заменяют различные схемы типа таблиц разрядов и классов, а также различные методические приемы. Например, такой прием, как определение количества цифр в числе. Используя его, ученик определяет количество цифр, ориентируясь на высший разряд.

Умение называть количество единиц, десятков, сотен, тысяч требует усвоение разрядного состава числа и осознания того, что каждая разрядная единица в числе (за исключением первого разряда единиц) содержит 10 единиц низшего разряда. Следует заметить, что именно такое рассуждение оказывается наиболее доступным для младших школьников, чем «десять единиц каждого разряда составляют 1 единицу высшего разряда. Например, число 843 содержит 843 единицы, т.е. оно состоит из 8 сотен или 800 единиц, 4 десятков равных 40 единицам и 3 единиц. В этом числе всего 84 десятка. Чтобы определить количество десятков в числе, нужно закрыть цифру, стоящую в разряде единиц. Аналогично определяется количество тысяч, десятков тысяч и так далее в любом числе.

При изучении нумерации многозначных чисел, дети знакомятся с приемами умножения и деления на 10, 100, 1000.

Вопрос 5. Методика ознакомления со сложением и вычитанием.

В действующем курсе математики начальных классов находит отражение теоретико-множественный подход к истолкованию сложения и вычитания целых неотрицательных чисел (натуральных и нуля), в соответствии с которым сложение целых неотрицательных чисел связано с операцией объединения попарно непересекающихся конечных множеств, вычитание – с операцией дополнения выделенного подмножества.

Этот подход легко интерпретируется на действиях с предметами, для выполнения которых учитель предлагает детям различные реальные ситуации. Можно условно выделить три вида ситуаций, которые связаны с операцией объединения:

a) увеличение данного предметного множества на несколько предметов;

b) увеличение на несколько предметов множества, равночисленного данному;

c) составление одного предметного множества из двух данных.

В процессе выполнения предметных действий у ребенка формируется представление о сложении как о действии, которое связано с увеличением количества предметов.

Указанием к выполнению предметных действий может являться задание «Покажи…». Например, учитель предлагает задание: «У Коли было 4 марки. Ему подарили еще две. Покажи, сколько марок стало у Коли».

Далее учитель показывает им, как можно записать выполнение действий математическими знаками, используя для этой цели цифры, знаки «+», «=». Целесообразно уже на этом этапе употреблять термины «выражение», «равенство».

Для разъяснения смысла сложения можно также опираться на представления детей о соотношении целого и его частей. В этом случае для вышеприведенной ситуации все марки Коли (целое) будут состоять из двух частей: марки, которые у него «были» и марки, которые ему «подарили».

Обозначая целое и части их числовыми значениями, дети получают выражение (4+2) или равенство (4+2=6) В системе РОД используется выражение А+В=С, где А и В – части, а С – целое.

В процессе выполнения предметных действий, соответствующих ситуациям вида b, у них формируется понятие «больше на», представления о котором связаны с построением совокупности, равночисленной данной («взять столько же») и ее увеличением на несколько предметов («и еще»).

При формировании у детей представления о вычитании, можно условно ориентироваться на следующие предметные ситуации:

a) уменьшение данного множества на несколько предметов;

b) уменьшение множества, равночисленного данному, на несколько элементов;

c) сравнение двух множеств.

В процессе выполнения предметных действий у младших школьников формируется представление о вычитании, как о действии, которое связано с уменьшением количества предметов.

Для разъяснения смысла вычитания можно использовать их представления о соотношении целого и части: часть всегда меньше целого, поэтому нахождение части всегда связано с вычитанием. Сформировать у учащихся представления о смысле действий сложения и вычитания является необходимым условием для правильного выбора действий при решении текстовых задач.

Вопрос 6. Методика изучения сложения и вычитания в пределах 10.

Для нахождения результатов при сложении и вычитании знакомятся с различ­ными вычислительными приемами. Любой вычислительный прием можно представить в виде последовательности операций, выполнение каждой из которых связано с теми или иными математическими понятиями. Приемы сложения и вычитания в пределах 10 рассматриваются в 4 этапа. Каждый этап этой последовательности тесно связан с предыдущими этапами, и предполагает их усвоение.

1. При составлении таблиц «а+1» и «а-1» ученики пользуются приемом присчитывания и отсчитывания по единице, в основе которого лежит понятие отрезка натурального ряда чисел от 1 до 10 и принцип его образования.

2. Умение представлять числа 2, 3, 4 в виде суммы двух слагаемых позволяет им овладевать приемом присчитывания и отсчитывания по частям. Сначала они прибавляют и вычитают 2, отсчитывая и присчитывая по единице, опираясь на отрезок натурального ряда чисел от 1 до 10. Знание табличных случаев «а+2» и «а-2» дети могут использовать, прибавляя и вычитая по частям число 3 (3=2+1) и число 4 (4=2+2). Умение представлять число в виде суммы позволяет учащимся овладеть приемами присчитывания и отсчитывания по частям, которыми они пользуются при составлении таблиц второго этапа.

3. Знакомство с переместительным свойством сложения - основа такого вычислительного приема, как перестановка слагаемых. Но этот прием оказывается эффективным только в том случае, если ученики прочно усвоят табличные случаи сложения, рассматриваемые на втором этапе. Данный прием позволяет закреплять ранее изученные случаи сложения и устанавливать их связь с новыми, способствуя тем самым прочному усвоению состава каждого числа в пределах 10. Например: 6 – это 4 и 2, 2 и 4; 8 – это 5 и 3, 3 и 5.

4. Прочное усвоение состава каждого числа в пределах 10 – необходимое условие приема, основой которого является взаимосвязь компонентов и результата сложения.

Подготовка к усвоению этой связи проводится с самого начала работы над сложением и вычитанием. С этой целью предусматриваются специальные упражнения: по данному рисунку – один большой и два маленьких мяча - составить пример на сложение и вычитание; реши и сравни выражение 4 + 3 и 7 – 3. Знакомство со связью между слагаемыми и суммой происходит на отдельном уроке, где выполняются операции над множествами. Эти знания учащиеся используют, выполняя вычитание чисел, когда вычитаемое больше (равно) 5. Представляя уменьшаемое в виде суммы двух слагаемых, одно из которых равно вычитаемому, они рассуждают следующим образом: «Если из суммы вычесть одно слагаемое, то останется другое». Например: 9 – 5. 9 – это 4 и 5, если вычесть 5, то останется 4. Эти операции могут фиксироваться в различных формах записи или комментироваться.

Вопрос 7. Методика изучения сложения и вычитания однозначных чисел с переходом через десяток и соответствующие случаи вычитания.

Прием сложения однозначных чисел с переходом через десяток сводится:

а) к дополнению первого слагаемого до числа 10. Это первая операция, входящая в состав приема;

б) вторая операция связана с представлениями о смысле действий сложения и вычитания и с усвоением состава чисел в пределах 10. Опираясь на эти знания, учащиеся смогут ответить на вопрос – сколько единиц осталось во втором слагаемом после того, как выполнена первая операция;

в) третья операция – оставшиеся единицы прибавляются к числу 10.

Таким образом, для овладения данным приемом необходимо прочное усвоение детьми состава каждого числа в пределах 10 и состава двузначного числа из десятков и единиц. Этот прием можно представить в виде тождественных преобразований:

8+5=8+(2+3)=(8+2)+3= 10+3=13, при выполнении которых используется сочетательное свойство сложения или правило прибавления суммы к числу.

Но практика показывает, что большинство семилетних детей с трудом выполняет такую громоздкую запись, поэтому целесообразнее использовать другие формы записей. Например:

8+5=13 8+ 5 =13

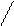
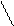8+2+3=13

2 3

Число 2 показывает, какое число нужно прибавить к 8, чтобы получить 10. Число 3 – сколько единиц нужно прибавить к 10.

Пользуясь новым вычислительным приемом, они постепенно составляют таблицу сложения в пределах 20, которую ученики должны прочно усвоить. Учителю следует иметь в виду, что для некоторых учеников процесс полного усвоения этих таблиц может быть длительным. Поэтому отработки навыков сложения и вычитания чисел в пределах 20 необходимо уделять внимание на всех последующих уроках.

В действующем курсе математики для вычитания однозначного числа из двузначного (в пределах 20) используются два приема. По своей сути они оба знакомы учащимся. В основе одного лежит понятие взаимосвязи суммы и слагаемых и прочное усвоение таблицы сложения в пределах 20:

12-7=5

12=7+5

В основе другого приема, который можно назвать «отсчитывание по частям», - понятие смысла действий.

12-7=12-(2+5)=(12-2)-5=10-5=5

Вопрос 8. Изучение сложения и вычитание в концентре «Сотня»

В результате изучения темы «Сложение и вычитание» учащиеся должны научиться осознанно выполнять сложение и вычитание любых чисел в пределах 100, твердо усвоить табличные случаи сложения и вычитания с переходом через десяток, а также ряд теоретических вопросов. Сначала рассматриваются устные приемы вычислений, затем письменные.

У с т н ы е п р и е м ы. Вычисления выполняются , начиная с единиц высшего разряда.

Сложение и вычитание рассматриваются в таком порядке:

1) Сначала изучается сложение и вычитание разрядных чисел 70+20, 60-40.

Сложение и вычитание двузначных разрядных чисел сводится к сложению и вычитанию однозначных чисел. Объяснение решения двух-трех примеров сопровождается иллюстрацией и такой записью:

70+2060-40

7 дес. + 2 дес. = 9 дес. 6 дес. - 4 дес. = 2 дес.

70 + 20 = 90 60-40=20

В учебнике Аргинской И.И. (РОЗ) такие приемы раскрываются на основе сравнения со случаями 7+2 и 6 – 4.

Далее рассматриваются правила прибавления и вычитания числа и суммы и на их основе вводятся вычислительные приемы.

Первое правило - прибавление числа к сумме.

Введению свойства прибавления числа к сумме должна предшествовать специальная подготовительная работа, в результате которой учащиеся знакомятся с математическими выражениями «сумма чисел...» и «разность чисел...», учатся читать и записывать выражения со скобками, заменять двузначные неразрядные числа суммой их разрядных слагаемых. Эти вопросы рассматриваются при изучении сложения и вычитания в пределах 10 и нумерации чисел в пределах 100.

Изучение каждого свойства строится примерно по одному плану: сначала, используя наглядные пособия, надо раскрыть суть самого свойства, затем научить детей применять его при выполнении различных упражнений учебного характера, и, наконец, научить, пользуясь знанием свойства, находить рациональные приемы вычислений с учётом особенностей каждого конкретного случая.

Как только будет усвоено свойство, можно переходить к изучению вычислительных приемов, основанных на соответствующем свойстве.

Методика работы над каждым вычислительным приемом строится примерно по одному плану: сначала ведется подготовка к ознакомлению с приемом, затем вводится приём и выполняются упражнения, направленные на формирование умения применять приём в разных конкретных условиях и на формирование вычислительного навыка.

Рассмотрим, как можно провести работу над приёмами для случаев:

2) 46+20 и 46+2, которые вводятся после усвоения учащимися свойства прибавления числа к сумме.

В качестве подготовки предлагается решение удобным способом примеров вида:

(50 + 3) + 40 и (30 + 6) + 2. При решении примеров учащиеся должны уяснить, что удобнее десятки прибавлять к десяткам, а единицы к единицам. При ознакомлении с приемом надо, выполняя соответствующие действия, опираться на наглядность, сопровождая их записями и словесными пояснениями.

Важно с самого начала научить детей выделять при решении примеров главные моменты:

26+4= (20+6)+4=20+(6+4)=20+10=30 – частный случай

3) Случаи вида 48-30, 48-3, 30-6основаны направиле вычитания числа из суммы.

48-30=(40+8)-30=(40-30)+8=10+8=18

48-3=(40+8)-3=40+(8-3)=40+5=45

30-6=(20+10)-6=20+(10-6)=20+4=24 – частный случай

Основным способом введения вычислительного приема является показ образца действия, который в некоторых случаях разъясняется на предметном уровне, а затем закрепляется в процессе тренировочных упражнений.

4)47+5 –вычислительный прием основан направиле прибавления суммы к числу.

В данном случае второе слагаемое заменяется суммой удобных слагаемых:

47+5=47+(3+2)=(47+3)+2=50+2=52

5) 42-5– в основе приема– правило вычитания суммы из числа

42-5=42-(2=3)=(42-2)-3=40-3=37

6)40+16, 40-16 –основаны направилах прибавления суммы к числу и вычитания суммы из числа:

40+16=40+(10+6)=(40+10)+6=50+6=56

40-16=40-(10+6)=(40-10)-6=30-6=24

7)Наиболее сложные случаи: 45+12, 45-12 –основаны направилах прибавления суммы к числу и вычитания суммы из числа:

45+12= 45+(10+2)=(45+10)+2=55+2=57

45-12=45-(10+2)=9=(45-10)-2=35-2=33

П и с ь м е н н ы е п р и е м ы .Вычисления выполняются, начиная с единиц низшего разряда.

1) Сначала рассматриваются случаи сложения и вычитания без перехода через разряд. Используя счетные палочки, обосновываются письменные приемы 34+23, 56-32.Дается алгоритм.

4+3=7 34

30+20=55 +23

50+7=57 57

Объяснение:

1) Пишудесятки под десятками, единицы под единицами.

2) Складываю единицы: 4+3=7, пишу 7 под единицами.

3) Складываю десятки: 3+2=5, пишу 5 под десятками.

4) Читаю ответ: сумма равна 57

Аналогично

2) Затем рассматриваютсяслучаи с переходом через разряд: 49+23 72-34

Сначала повторяется устный прием вычисления, в строчку. Обращается внимание на неудобство счета, возможность ошибки: 49+23=49+(20+3)=69+3=72

72-34=72-(30+4)=42-4=38 Дается образец записи в столбик:

+23

Объяснение:

1) Пишу…

2) Складываю единицы:9+3=12; 12 – это 1дес. и 2ед.; пишу под единицами 2, а 1 десяток запомню и прибавлю к десяткам.

3) Складываю десятки: 4+2=6; 6 да еще 1, получится 7. Пишу 7 под десятками.

4) Читаю ответ: сумма равна 72

-34

Объяснение:

1) Пишу…

2) Вычитаю единицы:из 2 нельзя вычесть 4; беру 1 дес. из 7дес.(чтобы помнить об этом, ставлю точку над цифрой 7); 1дес.и 2ед – это 12. 12-4=8; пишу под единицами 8.

3) Вычитаю десятки.Стало не 7, а 6дес. 6-3=3.

4) Читаю ответ:разность равна 38

Случай90-36– частный, рассматривается аналогично предыдущему.

Вопрос 9. Сложение и вычитание трёхзначных и многозначных чисел

В концентре «Тысяча» последовательно рассматриваются устные приемы сложения и вычитания, а затем письменные.

Трёхзначные числа

Устные приемы: На подготовительном этапе приёмы основаны на знании нумерации:

а) 700 + 40, 820 + 8, 948 - 40, 948 - 8

б) 789 + 1, 870 - 1, 870 + 1, 699 + 1

в) 400 + 200, 400 - 200, 800 - 500, 800 + 500, 250 + 50, 250 - 50.

На первом этапе изучения приемов сложения и вычитания трёхзначных чисел учащиеся знакомятся с приёмами вида: 540 + 300, 540 - 300, 540 + 30, 540 - 30. Дети повторяют правила прибавления числа к сумме и вычитания числа из суммы, выполняя знакомые упражнения с двузначными числами. Учащиеся устанавливают, что эти приёмы схожи.

Можно показать другой прием:

540 + 30 / 54 дес. + 3 дес. = 57 дес.

540 - 300 / 54 дес. - 30 дес. = 24 дес.

Этот прием подготавливает детей к изучению приёмов умножения и деления в пределах 1000.

На втором этапе рассматриваются случаи сложения и вычитания, основанные на использовании правил прибавления суммы к числу и вычитания суммы из числа.

430 + 210 = 430 + (200 + 10) = (430 + 200) + 10 = 640

Также используется приемы поразрядного сложения и вычитания:

430 + 210 = (400 + 30) + (200 + 10) = (400 + 200) + (30 + 10) = 640.

Также дети рассматривают сложение и вычитание с переходом через разрядную единицу: второе слагаемое представляют в виде суммы удобных слагаемых, которая дополняет первое слагаемое до простых сотен.

280 + 160 = 280 + (20 + 140) = (280 + 20) + 140 = 440.

Письменные приёмы: Сначала изучаются письменные приемы сложения, а затем - вычитания. Подготовительная работа начинается с повторения действий для двузначных чисел.

Повторяют правило прибавления суммы к сумме. Затем это правило применяется для сложения двух сумм из трёх слагаемых: (300 + 40 + 5) + (200 + 20 + 4). Дети выясняют, что удобнее складывать сотни с сотнями, десятки - с десятками, а единицы - с единицами. Подготовительная работа закончена.

Первыми рассматриваются примеры на сложение без перехода через разрядную единицу. Сначала примеры вида 232 + 347 решаются устно с подробной записью в строчку, а затем - в столбик. При решении примеров вида 427 + 133, 363 + 245 легко показать, почему письменное сложение нужно начинать не с высших разрядов, а с единиц первого разряда.

Работа над письменными приемами вычитания строится аналогично.

Наиболее трудными являются примеры вида: 900 - 547, 906 - 547.

Многозначные числа

Основными задачами учителя являются: обобщить и систематизировать знания учащихся о действиях сложения и вычитания, закрепить навыки устного сложения и вычитания, выработать осознанные и прочные навыки письменных вычислений.

Подготовительная работа начинается при изучении нумерации многозначных чисел. Повторяют устные приёмы сложения и вычитания и свойства действий, на которые они опираются: 8400 + 600, 9800 - 700 ...

Повторяют письменные приемы сложения и вычитания трёхзначных чисел.

6 сот. + 8 сот. = 14 сот. = 1 тыс. 4 сот.

При ознакомлении с письменным сложением и вычитанием многозначных чисел учащиеся решают такие примеры, где каждый последующий включает в себя предыдущий:

752 + 246, 4752 + 3246, 54752 + 43246, 837 - 425, 6837 - 2425, 76837 - 52425.

Ребята приходят к выводу, что сложение и вычитание многозначных чисел выполняется так же, как и трёхзначных.

Далее рассматриваются случаи постепенного увеличения числа переходов через разрядную единицу, включаются случаи, где в уменьшаемом содержатся нули, изучается сложение нескольких слагаемых, а также сложение и вычитание величин.

Трудность представляют случаи вычитания, когда уменьшаемое выражено разрядным числом.

400100 - 205708.

Из нуля единиц мы не можем вычесть 8 единиц. Берем одну сотню и раздробляем её в десятки. В 1 сотне - 10 десятков, берём из 10 десятков 1 десяток. Раздробляем десяток в единицы, получаем 10 единиц.

Больше внимания должно уделяться устным вычислениям, а то даже в простых примерах дети будут вычислять письменно.

Вслед за изучением сложения и вычитания многозначных чисел приступают к сложению и вычитанию величин, которое выполняется, как и с отвлечёнными числами

Вопрос 10. Методика первоначального ознакомления с действием умножения. Методика ознакомления с названиями чисел при умножении и зависимость между ними.

Необходимость введения нового действия осознается учащимися в процессе рассмотрения различных ситуаций. Например, учащимся предлагается схематический чертёж поля прямоугольной формы, которое разбито на равные участки (квадраты). Нужно определить, на сколько участков (квадратов) разбито данное поле.

Они самостоятельно приходят к выводу, что достаточно посчитать число квадратов в одном ряду (их 11) и повторить это число слагаемыми 4 раза (11+11+11+11). Можно также предложить ситуации с величинами: цена, кол-во, стоимость. Например: один батон стоит 10 р. Сколько нужно заплатить денег за 2 батона? (10+10). За три батона? (10+10+10). За 12 батонов (10+10+10+...). Такую длинную запись можно выполнить иначе: 10х12. Определяя умножениекаксложение одинаковых слагаемых и показывая новую математическую запись, учитель, используя действия с предметами разъясняет детям значение каждого числа в этой записи. Особенно важно обратить их внимание на то, что число, на которое мы умножаем, показывает, сколько раз первое число повторяется слагаемым.

Для усвоения учащимися смысла умножения можно использовать упражнения:

а) выполнение рисунка по данной математической записи

б) выполнение математической записи, соответствующей рисунку

в) соотнесение математической записи и рисунка

Так же, как и при сложении, полезно при разъяснении смысла умножения предлагать ученикам задания, в процессе выполнения которых у них может возникнуть догадка о закономерности, связанной с переместительным свойством умножения.

г) замена произведения суммой

д) замена суммы произведением

е) сравнение числовых выражений

ж) сравнение двух произведений, значение одного из которых известно (Используя первое равенство, найдите значение второго произведения).

Затем вводятся названия компонентов при умножении :

множительмножительпроизведение

8 * 4 = 32

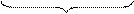
произведение

и рассматривается зависимость между ними. С этой целью можно использовать подвижные карточки.

Составляется пример на умножение, записывается широко на доске:

3 * 2 = 6

Учитель предлагает назвать компоненты умножения. Появляются карточки:

3 * 2 = 6

множитель множитель произведение

По данному примеру на умножение составляются 2 примера на деление:

6 : 2 = 3

6 : 2 = 3

Дети называют числа так, как они назывались в первом примере,учитель крепит карточки:

6 : 2 = 3

произведение множитель множитель

6 : 2 = 3

произведение множитель множитель

Теперь зависимость дети могут увидеть сами: если произведение двух чисел разделить на один из множителей, то получим другой множитель.

Для обоснования частных случаев вида 1∙ аи0∙ адетям предлагается задание:

Найди результат, пользуясь сложением:

1 ∙ 2, 1 ∙ 3, 1 ∙ 4, 1 ∙ 6, 1 ∙ 7

0 ∙ 2, 0 ∙ 6, 0 ∙ 3, 0 ∙ 5

После выполнения задания делается вывод.

Случаи а∙ 1, а∙ 0 запоминаются (так договорились), так как их нельзя объяснить, используя конкретный смысл умножения (нет повторяемости слагаемых)

Вопрос 11. Методика обучения решению простых задач на умножение и деление, в которых задано отношение «больше в…», «меньше в…»

При введении любой задачи выделяется три этапа: подготовительный, ознакомление, закрепление. Перед рассмотрением задачи на увеличение в несколько раздети знакомятся со смыслом отношения «больше в…». При этом можно использовать наглядность: «Положите в первый ряд 4 треугольника. Ниже положите 2 раза по столько кругов, сколько треугольников в первом ряду. В этом случае говорят: кругов в 2 раза больше, чем треугольников, а треугольников в 2 раза меньше, чем кругов». Дети не могут не видеть, что смысл отношения «больше в несколько раз» тесно связан с умножением: совокупность предметов увеличивается, мы 4 кружка повторяем 2 раза.Делается вывод: если говорят «больше в …», надо умножить.

На этом же уроке вводится текстовая задача: « Для детского сада купили 4 зеленых мяча, а красных в 3 раза больше. Сколько красных мячей купили?»

З. – 4 м.

К. - ?, в 3 раза Б.

Выбор действия: «Если сказано в3 раза больше, то каким действием будем решать?»

Решение записывается. Вместо традиционной краткой записи можно использовать схему (отрезки).

В некоторых образовательных направлениях («Школа 2000», «Нач. школа XXI век») одновременно с задачей на увеличение в несколько раз в прямой форме, вводится косвенная форма: «Купили 4 зеленых мяча, это в 3 раза меньше, чем красных. Сколько красных мячей купили?»

З. – 4 м., в 3 раза М.

К. - ?

Ребенок должен понимать обратную связь: если зеленых мячей в 3 раза меньше, то красных в 3 раза больше. «Больше в…», значит, надо умножить.

Чтобы дети не путали задачи, связанные с отношениями «больше в…» и «больше на…» следует научить их при выборе действия ориентироваться на предлог: «на… больше» - значит выполняем сложение, «в…больше» - значит умножение. Решение задач этих видов следует перемежать.

Смысл отношения «меньше в…» связан с делением на равные части.

«В первом ряду 8 кружков, во второй надо положить в 4 раза меньше»

Используется наглядность: чтобы получить в 4 раза меньше кружков, чем 8, разделим 8 кружков на 4 равные части и возьмем столько, сколько их в одной такой части. Дети подводятся к выводу: если говорится «меньше в…», выполняется деление. Работа над текстовой задачей аналогична предыдущему виду.

Следует иметь ввиду, что прочное сравнение двух чисел, связанное с ответом на вопрос: «Во сколько раз одно число больше (меньше) другого?»фактически сводится к делению по содержанию.

Рассмотрим, например, такую ситуацию: «У Коли 10 тетрадей, у Пети - 2. Во сколько раз у Коли тетрадей больше, чем у Пети?»

Для того, чтобы ответить на этот вопрос, нужно узнать, сколько раз 2 содержится в 10. Для этого необходимо выполнить деление по содержанию: 10:2 = 5(раз).

Число 5 означает, что 2 содержится в 10 5 раз. Значит 10 больше 2 в 5 раз, и 2 меньше 10 в 5 раз.

Вывод: чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее.

Вопрос 12. Раскрытие смысла деления и методика изучения зависимости между числами при делении. Частные случаи деления с 0 и 1.

Основа формирования у младших школьников представлений о смысле деления - теоретико-множественный подход к трактовке частного, суть которого сводится к разбиению конечных множеств на равночисленные множества, не имеющих общих элементов.

Выбор подхода обусловлен тем, что он позволяет опирать на жизненный опыт ребёнка при введении новой терминологии и математической записи. Действительно, большинство учащихся легко справляются с таким практическим заданием: «Раздай 10 яблок по 2 каждой девочке. Сколько девочек получат яблоки?».

Наглядное изображение выполняемых действий помогает ребенку осознать их математический смысл.

Он сводится к разбиению конечного множества яблок на равночисленные множества (по 2 яблока). В результате - получаем число частей в этом разбиении. На языке, доступном младшему школьнику, это означает, что он разделил яблоки на части, по 2 в каждой, т.е. узнал, «сколько раз по 2 содержится в 10». Выполненное действие в математике принято записывать так: 10 : 2 = 5 ( десять разделить на 2 - получится 5).

Доступно им и такое задание: «Раздай 10 яблок поровну двум девочкам. Сколько яблок получит каждая?»

В данной ситуации учащиеся могут действовать по-разному:

а) Одни будут брать по одному яблоку и раздавать их по очереди, сначала одной девочке, потом другой, пока не раздадут все яблоки.

б) Другие могут сразу взять 2 яблока, т.к. девочек две и разделить между ними эти яблоки, затем так же поступить со второй парой яблок, с третьей и т.д., пока все не раздадут.

В результате выполнения описанных действий множество всех яблок будет разделено на 2 равные части, численность каждой из которых равна 5.

Процесс деления на равные части довольно трудно изобразить на рисунке, но когда деление выполнено практически и определена численность каждой части, рисунок можно использовать для того, чтобы учащиеся осознали результат выполненного предметного действия.

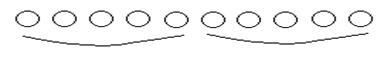
Таким образом, частное может обозначать число частей, на которое разделили данное количество яблок ( при этом делили поровну, по 2 в каждой части ). Этот случай деления в методике математики принято называть «делением по содержанию», но частное может обозначать количество яблок в каждой части (при этом делили опять же поровну, на 2 равные части). Этот случай называют «делением на 2 равные части».

В практике начального обучения принято сначала рассматривать ситуации, связанные только с первым случаем деления, затем уже со вторым. Некоторые учителя вводят даже термины «деление по содержанию» и «деление на равные части», требуя от школьников узнать каждый случай деления и назвать его, употребляя при этом соответствующие термины. При этом, когда выполняется «деление по содержанию», требуется говорить, что «10 разделили по 2», когда выполняется «деление на равные части», требуется говорить, что «10 разделили на 2». Но при чтении числовых равенств «10:2=5; 8:4 = 2) целесообразно пользоваться формулировкой (10 разделить на 2, 8 разделить на 4). Термин «разделить по» употребляется тогда, когда речь идет о конкретных предметах и связан с особенностями русского языка. Например, по-русски не говорят «10 яблок разделить на 2 яблока», говорят так «10 яблок разделить по 2 яблока». Так как при чтении числового равенства мы не называем предметы, поэтому можно сказать: «10 разделить на 2, получим 5». Поэтому не следует вводить термины «деление по содержанию» и «деление на равные части», т.к. математический смысл одного и другого случая деления сводится к разбиению данного множества на равночисленные подмножества. Но учителю необходимо знать эти термины, чтобы учитывать оба случая при подборе практических заданий и ситуаций, нацеленных на формирование представлений о смысле деления.

При изучении зависимости между компонентами деления можно использовать подвижные карточки. Сначала составляется пример на деление, называются компоненты:

8 : 2 = 4

делимое делитель частное

Затем учитель предлагает детям составить еще один пример на деление и на умножение с этими же числами. Примеры записываются, компоненты называются так же, как в первомпримере:

8 : 4 = 2

делимое частное делитель

4∙2 = 8

частное делитель делимое

Под руководством учителя дети делают вывод: если делимое разделить на частное, получится делитель. Если частное умножить на делитель, получится делимое.

Частные случаи деления с 1 и 0 основываются на взаимосвязи деления и умножения:

3:1 = 5:1= 18:1= 25:1=

1 ∙ 3 = 3 1∙ 5 = 5 1∙18 = 18 1 ∙ 25 = 25

Рассуждение: разделить 3 на 1 – значит, найти такое число, при умножении на которое 1 получится 3. Это число 3. Значит, 3:1=3. После рассмотрения нескольких частных случаев делается вывод: при делении любого числа на единицу в частном получается то число, которое делили.

0:2=0, так как 0*2=0;

0:8=0, так как 0*8=0

Вывод: при делении нуля на любое другое число получается нуль.

Делить на нуль нельзя. 5:0 – значит, надо найти такое число, при умножении которого на 0 получится 5.Такого числа нет.

Вопрос 13. Обучение табличному умножению и делению

Знание таблицы умножения и деления является основой формирования вычислительных навыков учащихся. Ее изучение начинается с таблицы умножения двух. Вначале (первый этап) составляется таблица умножения двух, которую дети должны будут постепенно запомнить. Другие таблицы составляются несколько позднее. Это позволяет рассредоточить во времени изучение материала, который надо запомнить наизусть.

При составлении таблицы умножения двух результат находят сложением, используя при этом наглядные пособия, например, квадрат с уголком, или обводят в тетради 9 рядов клеток, по 2 клетки в ряду. Составление этой таблицы можно осуществить по частям:

1) 2 ∙ 2= 2+2=4

2 ∙ 3= 2+2+2=6

2 ∙ 4= 2+2+2+2=8

2 ∙ 5= 2+2+2+2+2=10

Дети замечают, что результат следующего произведения на 2 больше предыдущего. Эту закономерность можно использовать при получении остальных случаев:

2) 2 ∙ 6= 12 10+2=12

2 ∙ 7=14 12 +2=14

2 ∙ 8=16 14+2=16

2 ∙ 9=18 16+2=18

Получилась таблица умножения двух, которую дети должны постепенно запомнить.

На основе переместительного свойства умножения составляется таблица умножения на два. Ученикам предлагается самим составить эту таблицу, пользуясь известной им таблицей умножения двух.

На основе связи между произведением и множителями рассматриваются табличные случаи деления с числом 2. Ученики записывают по памяти известную им таблицу умножения на 2. Затем, используя знание связи между компонентами и результатом действия умножения, находят результаты соответствующих случаев деления. Получается запись:

2 ∙ 2 = 4 4 : 2 = 2

2 ∙ 3 = 6 6 : 2 = 3 6 : 3 = 2

2 ∙ 4 = 8 8 : 2 = 4 8 : 4 = 2 и т.д.

Ученики рассуждают: произведение чисел 2 и 3 равно 6; если произведение 6 разделить на первый множитель 2, то получится второй множитель 3, а если произведение 6 разделить на второй множитель 3, то получится первый множитель 2 и т.д.

Чтобы усвоили рассмотренные случаи деления с числом 2, их надо чаще включать в устные упражнения и письменные работы.

Знания о действиях умножения и деления, а также умения, полученные на первом этапе, являются основой изучения на втором этапе табличных случаев умножения и соответствующих случаев.

Вопрос 14. Методика изучения внетабличных случаев умножения и деления в концентре «Сотня»

Задачи изучения темы

1. Познакомить учащихся со свойствами арифметических действий (умножение и деление суммы на число) и сформировать умение пользоваться ими при устных вычислениях.

2. Усвоить приемы устных вычислений в пределах 100 при умножении двузнач­ного числа на однозначное и однозначного на двузначное, при делении двузначного числа на однозначное и двузначное.

3. Сформировать умение выполнять устные вычисления для случая деления с остатком.

При объяснении каждого из свойств учитель использует дидактические материалы, наглядные пособия, иллюстрации учебника.

В основе формирования вычислительных приемов лежит усвоение различных вопросов курса математики начальных классов.