Дисперсія випадкової величини
На практиці зустрічаються випадкові величини, які мають однакові математичні сподівання, але відхилення значень від математичного сподівання є зовсім різним. Тому необхідно ввести числову характеристику, яка задає розсіювання випадкової величини навколо математичного сподівання. Такою характеристикою буде дисперсія.
Означення 11.3. Дисперсією випадкової величини називається математичне сподівання квадрата відхилення цієї величини від її математичного сподівання, тобто
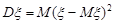 . (11.3)
. (11.3)
Відхилення 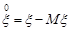 назвемо центрованою випадковою величиною, яка відповідає величині
назвемо центрованою випадковою величиною, яка відповідає величині  . Зрозуміло, що
. Зрозуміло, що 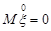 . За допомогою центрованої випадкової величини формулу (11.3) можна записати коротше
. За допомогою центрованої випадкової величини формулу (11.3) можна записати коротше
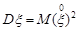 .
.
Для дискретної випадкової величини формула (11.3) розписується так:
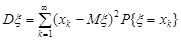 . (11.4)
. (11.4)
Зауваження. Помітимо, що ряд (11.4) має тільки додатні члени, тоді він може збігатися і, отже, дисперсія випадкової величини  буде скінченою. Цей ряд може розбігатися до
буде скінченою. Цей ряд може розбігатися до 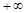 , тоді дисперсія величини
, тоді дисперсія величини  – необмежена. Отже, дисперсія будь-якої дискретної випадкової величини, як міра розсіювання можливих значень випадкової величини, завжди існує та є або скінченою невід’ємною величиною, або необмеженою. Зрозуміло, що всі ці висновки мають місце при умові існування математичного сподівання випадкової величини
– необмежена. Отже, дисперсія будь-якої дискретної випадкової величини, як міра розсіювання можливих значень випадкової величини, завжди існує та є або скінченою невід’ємною величиною, або необмеженою. Зрозуміло, що всі ці висновки мають місце при умові існування математичного сподівання випадкової величини  .
.
Якщо величина  набуває лише скінчену множину значень, то ряд (11.4) буде скінченою сумою.
набуває лише скінчену множину значень, то ряд (11.4) буде скінченою сумою.
Якщо  – неперервна випадкова величина, то формула (11.3) набуває вигляду:
– неперервна випадкова величина, то формула (11.3) набуває вигляду:
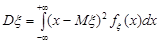 . (11.5)
. (11.5)
Аналогічне зауваження можна зробити відносно дисперсії неперервної випадкової величини.
Дисперсія, з точки зору механічної інтерпретації, дорівнює моменту інерції розподілення одиничної маси відносно центра тяжіння (математичного сподівання) цієї маси.
Наведемо основні властивості дисперсії.
1. Дисперсія сталої величини завжди дорівнює нулю, тобто DC = 0, де C – будь-яка стала.
Властивість очевидна, оскільки стала величина не має ніякого розсіювання.
2. Постійний множник виноситься за знак дисперсії в квадраті, тобто 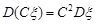 .
.
Доведення. За формулою (11.3) і властивістю 1 математичного сподівання випадкової величини
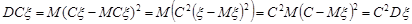 .
.
3. Дисперсія будь-якої випадкової величини дорівнює
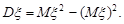
Доведення. За означенням (11.3)
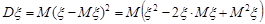 =
=
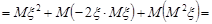
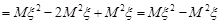 .
.
Цю властивість часто використовують для обчислення дисперсії. Для дискретної випадкової величини вона набуває вигляду:
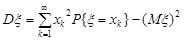 .
.
А для неперервної випадкової величини  вона записується так:
вона записується так:
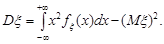
4. Якщо 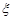 та
та 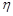 – незалежні випадкові величини, то
– незалежні випадкові величини, то
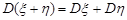 .
.
Доведення. Враховуючи попередню властивість дисперсії та властивості математичного сподівання, маємо
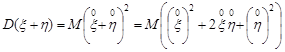 =
=
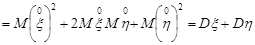 .
.
Наведемо деякі приклади обчислення дисперсії.
Приклад 11.3. За умовою задачі прикладу 9.2 обчислити дисперсію випадкової величини  , яка задає кількість влучень при трьох пострілах.
, яка задає кількість влучень при трьох пострілах.
Розв’язання. Беручи до уваги ряд розподілу випадкової величини  (приклад 9.2) та властивість 3 дисперсії, маємо
(приклад 9.2) та властивість 3 дисперсії, маємо
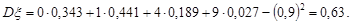
Приклад 11.4. В умовах прикладу 10.1 обчислити математичне сподівання неперервної випадкової величини  , яка розподілена за законом Сімпсона.
, яка розподілена за законом Сімпсона.
Розв’язання. Знаючи щільність розподілу ймовірностей випадкової величини  та математичне сподівання
та математичне сподівання 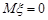 , за формулою (11.5) маємо
, за формулою (11.5) маємо
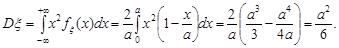

Розмірність математичного сподівання співпадає з розмірністю випадкової величини, а розмірність дисперсії – ні. Для того, щоб розмірність характеристики розсіювання була така сама, як розмірність випадкової величини, вводять середньоквадратичне відхилення ( або стандартне відхилення)
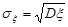 .
.
Дата добавления: 2016-11-02; просмотров: 3871;
