Ряды предпочтительных чисел (ГОСТ 8032-84)

Предпочтительными числами называются такие числа, которым отдается предпочтение по сравнению с другими.

Примеры использования предпочтительных чисел встречаются повсюду: размеры одежды и обуви, длина гвоздей, диаметр резьбы, номинальные значения масс гирь, мощность электрических машин, двигателей внутреннего сгорания и т. д.

Результатом использования предпочтительных чисел является такое согласование параметров и размеров, которое обеспечивает взаимозаменяемость деталей и узлов, создает предпосылки для гибких производственных систем, механизации и автоматизации производства, повышения производительности труда и в конечном итоге – повышения качества продукции.

Предпочтительным числам свойственны определенные математические закономерности. Наиболее простые ряды чисел строятся на основе арифметической прогрессии, в которой разность между последующим и предыдущим членами остается постоянной. Ряды, основанные на арифметической прогрессии, применяются сравнительно редко: ряд диаметров внутренних колец подшипников качения (через 5 мм), стандарты на размеры обуви. Преимуществом таких рядов является простота, а недостатком – относительная неравномерность. Например, в ряде из 100 членов разность – единица, но второй член относительно первого отличается на 100 %, десятый относительно девятого – на 11 %, а сотый относительно девяносто девятого – на 1 %. Таким образом, больших значений оказывается больше, чем маленьких, что не вполне соответствует потребностям.

Для преодоления этого недостатка может применяться ступенчатая арифметическая прогрессия, но гораздо чаще применяется геометрическая прогрессия, которая имеет важные преимущества:

1) постоянная относительная разность между любыми соседними членами ряда;

2) произведение или частное от деления любых двух членов прогрессии является новым членом ряда той же прогрессии.

Современный ряд предпочтительных чисел основан на геометрической прогрессии, которую в 1877 – 1879 гг. применил офицер французского инженерного корпуса Шарль Ренар при конструировании воздушных шаров. Ренар взял за основу канат имеющий массу а в граммах на 1 метр длины, и построил ряд, приняв знаменатель прогрессии, обеспечивающий десятикратное увеличение каждого пятого члена ряда, т. е. a g⁵ = 10 a, откуда g = .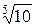

Получился следующий числовой ряд: a – 1,5849а – 2,5119а – 3,9811а – – 6,3096а – 10а. При этом а^к, где к – любое целое число и 0. При к = 0 получается ряд Ренара R5: 1 – 1,6 – 2,5 – 4 – 6,3 – 10.

Труд Ренара был опубликован в 1886 г., но тогда не привлек к себе внимания. Только в 1910 г. (Германия), 1912 г. (Франции) были утверждены стандарты по этим рядам.

По ГОСТ 8032-84 установлено четыре основных и два дополнительных ряда:

R5 → 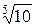= 1,5849 ≈ 1,6;

R10 → 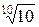= 1,2589 ≈ 1,25;

R20 → 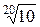= 1,12;

R40 → 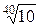= 1,0593 ≈ 1,06;

R80 → 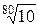= 1,0292 ≈ 1,03;

R160 → 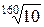= 1,015 ≈ 1,02.

На основе рядов предпочтительных чисел определены значения нормальных линейных размеров (ГОСТ 6636-69), из числа которых выбираются номинальные величины. Номинальным размером называется такой, значение которого определяется любым видом расчета и округляется в соответствии с ГОСТ 6636-69. Номинальный размер затем проставляется на чертеже в качестве основного.