Тести на наявність автокореляції.
При розв’язуванні задачі §2 було зроблено висновок про високу якість побудованої лінійної моделі парної регресії. Проте суттєвою обставиною є те, що всі оцінки і висновки отримані при умові, що виконуються передумови 1-4. Тому для достовірності прийнятих рішень необхідно перевірити виконання цих передумов. При цьому слід мати на увазі, що перевірці при МНК-оцінюванні підлягають лише передумови 2, 3, 4 (див. зауваження до рівності (2.21)). У випадку констатації невиконання хоча б однієї передумови модель класичної парної регресії перетворюється на економетричну модель і актуальними стають шляхи її дослідження.
1. Розпочнемо із перевірки виконання передумови 4 про нормальність розподілу випадкового збурення 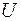 .
.
Якщо обсяг вибірки є дуже великим, тоді згідно з центральною граничною теоремою Ляпунова є підстави стверджувати виконання цієї передумови. У випадку малих вибірок ( 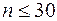 ) вже неправомірно робити такий висновок. Проблема також полягає у тому, що випадкова величина
) вже неправомірно робити такий висновок. Проблема також полягає у тому, що випадкова величина 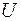 є неспостережуваною. Для отримання інформації про можливі значення цієї величини будемо виходити з двох обставин:
є неспостережуваною. Для отримання інформації про можливі значення цієї величини будемо виходити з двох обставин:
1) лінійності моделі (2.9)
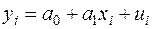 ,
, 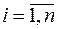 ;
;
2) отримання оцінок коефіцієнтів регресії 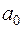 ,
, 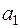 з допомогою МНК.
з допомогою МНК.
Тоді
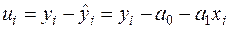 ,
, 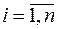 (3.1)
(3.1)
можна тлумачити як «спостережені» значення збурення 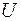 . Наявність лапок в слові «спостережені» зумовлене врахуванням двох попередніх обставин (лінійна модель може виявитись не найкращою, а оцінки
. Наявність лапок в слові «спостережені» зумовлене врахуванням двох попередніх обставин (лінійна модель може виявитись не найкращою, а оцінки 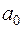 та
та 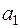 можуть отримуватися з допомогою інших методів).
можуть отримуватися з допомогою інших методів).
Отже, будемо вважати, що 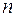 чисел
чисел 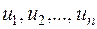 , визначені (3.1), відомі. Вони є можливими (спостереженими) значеннями випадкової величини
, визначені (3.1), відомі. Вони є можливими (спостереженими) значеннями випадкової величини 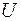 . Ставиться задача про перевірку статистичної гіпотези
. Ставиться задача про перевірку статистичної гіпотези 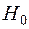 :
: 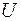 розподілена за нормальним законом (
розподілена за нормальним законом ( 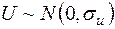 ). Якщо обсяг вибірки великий (див. [4]), то можна використати критерії узгодженості Пірсона або Колмогорова. Проте в багатьох випадках обсяги вибірки є малими, тому використаємо критерій Фішера.
). Якщо обсяг вибірки великий (див. [4]), то можна використати критерії узгодженості Пірсона або Колмогорова. Проте в багатьох випадках обсяги вибірки є малими, тому використаємо критерій Фішера.
В якості основних характеристик розподілу зручніше всього брати коефіцієнт асиметрії і ексцес:
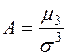 ,
, 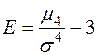 ,
,
де 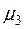 та
та 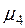 — центральні моменти третього та четвертого порядків відповідно. Для випадку нормального розподілу
— центральні моменти третього та четвертого порядків відповідно. Для випадку нормального розподілу 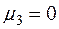 ,
, 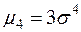 . Тому для цього розподілу виконуються рівності
. Тому для цього розподілу виконуються рівності
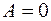 ,
, 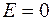 . (3.2)
. (3.2)
Відповідні вибіркові (емпіричні) коефіцієнти асиметрії і ексцесу визначаються формулами:
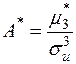 ,
, 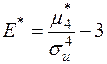 , (3.3)
, (3.3)
де центральний емпіричний момент 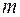 -го порядку
-го порядку 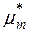 визначається за формулою (для даного випадку позначень):
визначається за формулою (для даного випадку позначень):
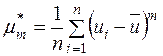 ,
, 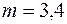 . (3.4)
. (3.4)
Емпіричні асиметрія і ексцес, як і всі числові характеристики нефіксованої вибірки, є випадковими величинами і тому навіть для нормального розподілу можуть відрізнятися від нуля. Закони розподілу 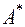 і
і 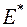 дуже складні і мало вивчені. Фішер запропонував модифікацію оцінок коефіцієнта асиметрії
дуже складні і мало вивчені. Фішер запропонував модифікацію оцінок коефіцієнта асиметрії 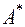 та ексцесу
та ексцесу 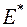 :
:
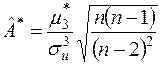 ,
, 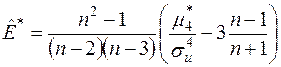 . (3.5)
. (3.5)
При невеликих обсягах вибірок 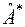 та
та 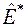 помітно відрізняються від
помітно відрізняються від 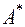 та
та 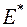 . Виявляється, що у випадку нормального розподілу оцінки
. Виявляється, що у випадку нормального розподілу оцінки 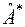 та
та 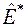 мають з великим ступенем точності нормальні випадкові розподіли, причому
мають з великим ступенем точності нормальні випадкові розподіли, причому 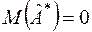 ,
, 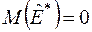 , а дисперсії визначаються виразами:
, а дисперсії визначаються виразами:
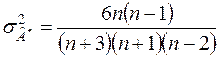 ,
, 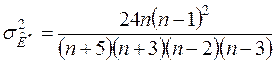 . (3.6)
. (3.6)
Отже, задача полягає у відповіді на питання: чи значуще оцінки 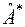 і
і 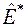 відрізняються від своїх математичних сподівань, тобто від нуля?
відрізняються від своїх математичних сподівань, тобто від нуля?
На практиці можна користуватися таким наближеним критерієм згоди:
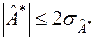 ,
, 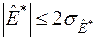 . (3.7)
. (3.7)
Задача 3.1. На основі статистичних даних задачі 2.1 здійснити перевірку виконання передумови 4 про нормальність розподілу випадкової величини 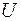 .
.
¡ Для знаходження 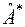 і
і 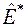 згідно з формулами (3.5) потрібно обчислити
згідно з формулами (3.5) потрібно обчислити 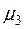 ,
, 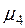 ,
, 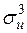 ,
, 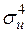 . Згідно з останнім рядком табл. 2.2
. Згідно з останнім рядком табл. 2.2 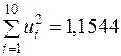 . Тому
. Тому 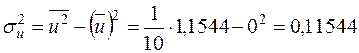 ,
, 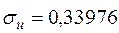 ,
, 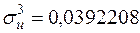 ,
, 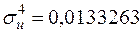 . Значення
. Значення 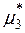 та
та 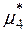 знайдемо за формулами (3.4). Для цього складемо розрахункову табл. 3.1, дані першого стовпця якої взяті з четвертого рядка табл. 2.2.
знайдемо за формулами (3.4). Для цього складемо розрахункову табл. 3.1, дані першого стовпця якої взяті з четвертого рядка табл. 2.2.
Таблиця 3.1
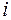
| 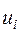
| 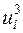
| 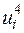
|
| 1 | -0,1938 | -0,0072788 | 0,0014106 |
| 2 | 0,7178 | 0,369837 | 0,265469 |
| 3 | -0,059 | -0,0002054 | 0,0000121 |
| 4 | -0,4474 | -0,0895546 | 0,0400667 |
| 5 | -0,3242 | -0,0340752 | 0,0110472 |
| 6 | 0,099 | 0,0009703 | 0,0000961 |
| 7 | -0,2894 | -0,0242379 | 0,0070145 |
| 8 | 0,4222 | 0,0752583 | 0,0317741 |
| 9 | 0,1338 | 0,0023953 | 0,0003205 |
| 10 | -0,0546 | -0,0001628 | 0,0000089 |
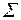
| 0,0044 | 0,2929462 | 0,3572197 |
Врахувавши, що 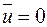 , отримаємо:
, отримаємо:
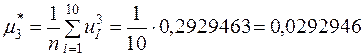 ,
,
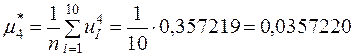 .
.
За формулами (3.5), (3.6) знаходимо:
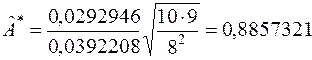 ,
,
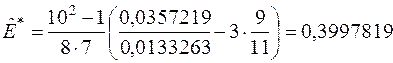 ,
,
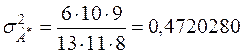 ,
, 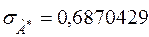 ,
,
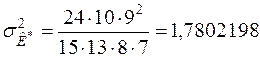 ,
, 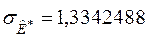 .
.
Обидві нерівності (3.7) виконуються:
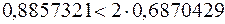 ,
, 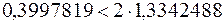 ,
,
а тому згідно з цим критерієм згоди гіпотеза 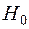 про нормальність закону розподілу
про нормальність закону розподілу 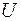 приймається. ¥
приймається. ¥
2. Друга передумова (гомоскедастичність або «однаковий розкид») передбачає виконання 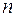 рівностей
рівностей
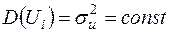 ,
, 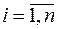 . (3.8)
. (3.8)
Якщо хоча б одна з цих рівностей не виконується, тобто
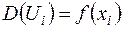 ,
, 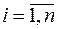 , (3.9)
, (3.9)
тоді має місце гетероскедастичність («неоднаковий розкид»).
Появу проблеми гетероскедастичності часто можна передбачити заздалегідь, ґрунтуючись на значенні характеру даних. Припущення про гомоскедастичність виправдане в тих випадках, коли досліджувані об’єкти є достатньо однорідними. Якщо ж досліджуються неоднорідні об’єкти, то, як правило, виникає проблема гетероскедастичності.
Приклади:
1) Якщо вивчається залежність прибутку фірми від розміру основних фондів, то природно очікувати, що для великих фірм коливання прибутку буде вищим, ніж для малих.
2) Якщо досліджується залежність витрат на харчування в родині від загального доходу, то розкид у даних буде більшим для родин із більш високим доходом.
Графічна форма розкиду спостережень залежить від форми зв’язку між 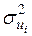 та
та 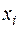 . Приклади зображені на мал. 3.1.
. Приклади зображені на мал. 3.1.

Малюнок 3.1.
У прикладних дослідженнях, як правило, використовується зручне припущення, що 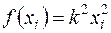 , де
, де 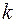 — стала, яку потрібно оцінити.
— стала, яку потрібно оцінити.
Розглянемо наслідки порушення передумови про гомоскедастичність. Можна довести, що оцінки коефіцієнтів регресії залишаються лінійними і незміщеними, але вже не володіють властивістю ефективності, тобто їх дисперсії вже не будуть мінімальними в класі лінійних оцінок. У зв’язку з цим розширюються довірчі інтервали. Як наслідок, тести Ст’юдента і Фішера-Снедокора дають неточні результати. Крім того, формулу для оцінки 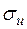 , строго кажучи, застосовувати вже не можна.
, строго кажучи, застосовувати вже не можна.
Отже, гетероскедастичність є серйозною проблемою. Досліднику потрібно знати: є вона чи немає. У випадку тестування гетероскедастичності вихідну модель необхідно модифікувати.
3. Виявляється, єдиних правил діагностування гетероскедастичності немає, а є різні тести з своїми недоліками та перевагами. Розглянемо найпростіші з них за змістом та розрахунками. В кожному тесті в якості нульової гіпотези розглядається 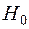 — гіпотеза про відсутність гетероскедастичності.
— гіпотеза про відсутність гетероскедастичності.
3.1. Тест рангової кореляції Спірмена передбачає найбільш загальні припущення про залежність дисперсій помилок регресії від значень незалежної змінної:
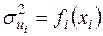 ,
, 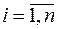 . (3.10)
. (3.10)
При цьому ніяких додаткових припущень відносно виду функцій 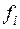 не робиться. Відмітимо також, що відсутнє обмеження стосовно закону розподілу помилок.
не робиться. Відмітимо також, що відсутнє обмеження стосовно закону розподілу помилок.
Ідея тесту полягає в тому, що абсолютні величини залишків регресії 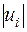 розглядаються як оцінки
розглядаються як оцінки 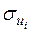 , тому при наявності гетероскедастичності
, тому при наявності гетероскедастичності 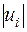 і значення
і значення 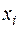 будуть корелювати. Проте кореляція в цьому випадку передбачається ранговою.
будуть корелювати. Проте кореляція в цьому випадку передбачається ранговою.
Рангова кореляція досліджується тоді, коли необхідно встановити силу зв’язку між ординальними (порядковими) змінними. Прикладами ординальних змінних є житлові умови, тестові бали, екзаменаційні оцінки. Джерелом ординальних змінних можуть бути і кількісні змінні, для яких здійснюється процес ранжування. Наприклад, кожну з двох множин чисел 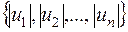 ,
, 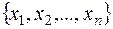 можна ранжувати в порядку зростання. В результаті
можна ранжувати в порядку зростання. В результаті 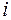 -тий об’єкт характеризується двома рангами
-тий об’єкт характеризується двома рангами 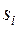 та
та 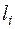 по змінних
по змінних 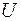 та
та 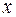 . Тоді коефіцієнт рангової кореляції Спірмена знаходиться за формулою
. Тоді коефіцієнт рангової кореляції Спірмена знаходиться за формулою
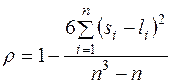 . (3.11)
. (3.11)
Якщо ранги всіх об’єктів рівні між собою, тобто 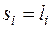
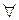
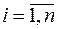 , то
, то 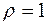 . Цей випадок називається повним прямим зв’язком. При повному оберненому зв’язку, коли ранги об’єктів по обох змінних розташовані в оберненому порядку, можна довести, що
. Цей випадок називається повним прямим зв’язком. При повному оберненому зв’язку, коли ранги об’єктів по обох змінних розташовані в оберненому порядку, можна довести, що 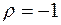 . У решті випадків
. У решті випадків 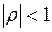 .
.
При перевірці значущості 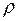 виходять із того, що у випадку правильності нульової гіпотези (про відсутність кореляційного зв’язку між змінними) при
виходять із того, що у випадку правильності нульової гіпотези (про відсутність кореляційного зв’язку між змінними) при 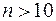 статистика
статистика
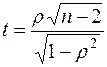 (3.12)
(3.12)
має 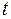 -розподіл Ст’юдента із
-розподіл Ст’юдента із 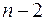 ступенями вільності. Тому
ступенями вільності. Тому 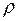 значущий на рівні
значущий на рівні 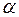 , якщо
, якщо
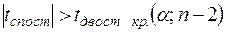 . (3.13)
. (3.13)
Задача 3.2. На основі статистичних даних задачі 2.1 на рівні 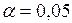 перевірити виконання передумови 2 з допомогою тесту рангової кореляції Спірмена.
перевірити виконання передумови 2 з допомогою тесту рангової кореляції Спірмена.
¡ Здійснимо ранжування змінних 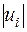 та
та 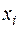 . Для цього складемо табл. 3.2, використавши дані табл. 2.1 (другий стовпець) та табл. 2.2 (передостанній рядок). При заповненні останнього стовпця вибирається найменше число в третьому стовпці і поруч з ним записується 1. Найменшому з тих чисел, що залишилися, відповідає 2, і т.д.
. Для цього складемо табл. 3.2, використавши дані табл. 2.1 (другий стовпець) та табл. 2.2 (передостанній рядок). При заповненні останнього стовпця вибирається найменше число в третьому стовпці і поруч з ним записується 1. Найменшому з тих чисел, що залишилися, відповідає 2, і т.д.
Таблиця 3.2
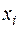
| 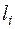 (ранг (ранг 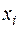 ) )
| 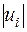
| 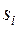 (ранг (ранг 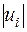 ) )
|
| 0,2 | 0,1938 | ||
| 0,3 | 0,7178 | ||
| 0,5 | 0,059 | ||
| 0,6 | 0,4474 | ||
| 0,8 | 0,3242 | ||
| 0,099 | |||
| 1,1 | 0,2894 | ||
| 1,2 | 0,4222 | ||
| 1,3 | 0,1338 | ||
| 1,4 | 0,0546 |
За формулою (3.11) знайдемо коефіцієнт рангової кореляції Спірмена:
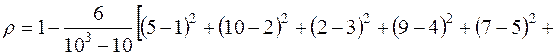
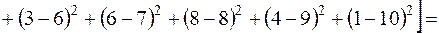
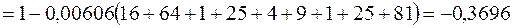 .
.
Згідно із (3.12)
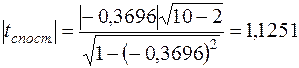 .
.
За табл. 3 додатків 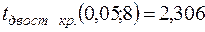 .
.
Оскільки на рівні 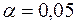 нерівність (3.13) не виконується, то нульова гіпотеза про відсутність кореляційного зв’язку є правильною. Отже, на цьому ж рівні приймається і гіпотеза
нерівність (3.13) не виконується, то нульова гіпотеза про відсутність кореляційного зв’язку є правильною. Отже, на цьому ж рівні приймається і гіпотеза 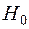 про відсутність гетероскедастичності (виконання передумови 2). ¥
про відсутність гетероскедастичності (виконання передумови 2). ¥
3.2. Тест Голдфелда-Квандта використовується у тому випадку, коли помилки регресії 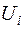 можна вважати нормально розподіленими випадковими величинами. При цьому спостережень має бути хоча б удвічі більше, ніж число оцінюваних параметрів. Як правило, тест застосовується до великих вибірок.
можна вважати нормально розподіленими випадковими величинами. При цьому спостережень має бути хоча б удвічі більше, ніж число оцінюваних параметрів. Як правило, тест застосовується до великих вибірок.
Припустимо, що середні квадратичні відхилення збурень 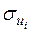 пропорційні значенням пояснюючої змінної
пропорційні значенням пояснюючої змінної 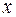 . Це означає постійність відносного, а не абсолютного, як у класичній моделі, розкиду збурень регресійної моделі.
. Це означає постійність відносного, а не абсолютного, як у класичній моделі, розкиду збурень регресійної моделі.
Впорядкуємо 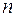 спостережень в порядку зростання значень
спостережень в порядку зростання значень 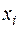 і виберемо
і виберемо 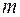 перших і
перших і 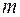 останніх спостережень (число
останніх спостережень (число 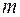 визначимо пізніше). Тоді гіпотеза про гомоскедастичність буде рівносильна тому, що значення
визначимо пізніше). Тоді гіпотеза про гомоскедастичність буде рівносильна тому, що значення 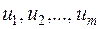 та
та 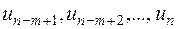 є вибірковими спостереженнями нормально розподілених випадкових величин, які мають однакові дисперсії.
є вибірковими спостереженнями нормально розподілених випадкових величин, які мають однакові дисперсії.
Зауваження. Для знаходження 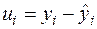 для двох груп (
для двох груп ( 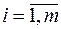 та
та 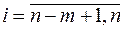 ) необхідно попередньо знайти два емпіричні рівняння для кожної з груп.
) необхідно попередньо знайти два емпіричні рівняння для кожної з груп.
Гіпотеза про рівність дисперсій двох нормально розподілених сукупностей, як відомо [4], перевіряється з допомогою критерія Фішера-Снедокора. Нульова гіпотеза про рівність дисперсій двох сукупностей по 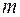 спостережень (тобто гіпотеза про відсутність гетероскедастичності) відкидається на рівні
спостережень (тобто гіпотеза про відсутність гетероскедастичності) відкидається на рівні 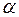 , якщо
, якщо
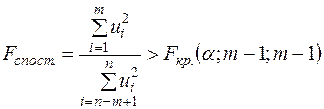 . (3.14)
. (3.14)
Відмітимо, що чисельник і знаменник в (3.14) слід було розділити на відповідне число ступенів вільності, проте в даному випадку ці числа однакові і рівні 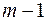 .
.
Виявляється, що коли вибрати 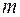 порядку
порядку 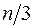 , тоді потужність тесту, тобто імовірність відкинути гіпотезу про наявність гомоскедастичності, коли насправді гетероскедастичності немає, буде максимальною.
, тоді потужність тесту, тобто імовірність відкинути гіпотезу про наявність гомоскедастичності, коли насправді гетероскедастичності немає, буде максимальною.
Задача 3.3. На рівні значущості 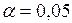 для задачі 2.1 перевірити виконання передумови 2 (ігноруючи малість вибірки) з допомогою тесту Голдфелда-Квандта.
для задачі 2.1 перевірити виконання передумови 2 (ігноруючи малість вибірки) з допомогою тесту Голдфелда-Квандта.
¡ За аналогією із розв’язуванням задачі 2.1. (п.1) знайдемо статистичні оцінки параметрів 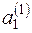 ,
, 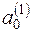 та
та 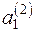 ,
, 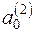 , виходячи з двох груп даних (
, виходячи з двох груп даних ( 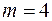 ):
):
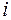
| 1 | 2 | 3 | 4 | 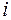
| 7 | 8 | 9 | 10 | ||
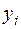
| 1,5 | 2,9 | 3,1 | 3,2 | 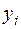
| 5,8 | 7,2 | 7,5 | |||
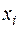
| 0,2 | 0,3 | 0,5 | 0,6 | 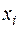
| 1,1 | 1,2 | 1,3 | 1,4 |
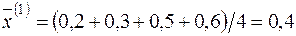 ;
;
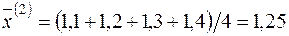 ;
;
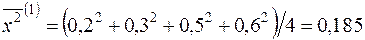 ;
;
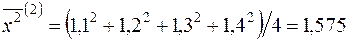 ;
;
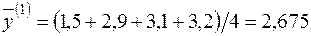 ;
;
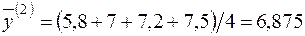 ;
;
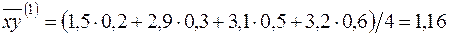 ;
;
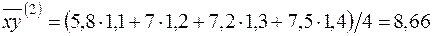 ;
;
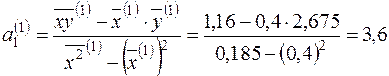 ;
;
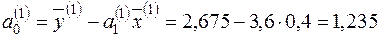 ;
;
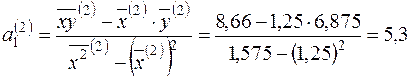 ;
;
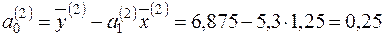 .
.
Отже, емпіричне рівняння для першої групи має такий вигляд:
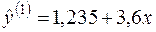 ,
,
а другої
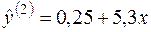 .
.
Тоді
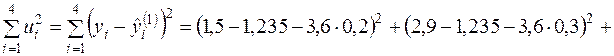
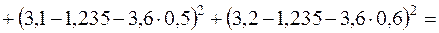
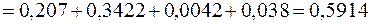 ;
;
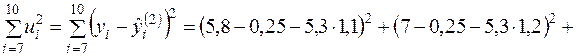
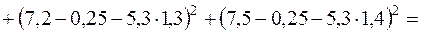
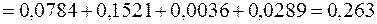 ;
;
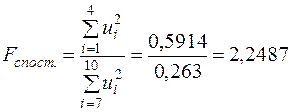 .
.
Врахувавши, що 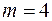 ,
, 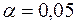 , за табл. 5 додатків знайдемо
, за табл. 5 додатків знайдемо 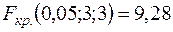 .
.
Оскільки 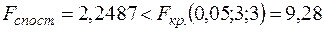 , тобто нерівність (3.14) не виконується, то робимо висновок, що гіпотеза
, тобто нерівність (3.14) не виконується, то робимо висновок, що гіпотеза 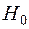 про відсутність гетероскедастичності на рівні
про відсутність гетероскедастичності на рівні 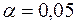 приймається.
приймається.
Отже, за тестом Голдфелда-Квандта на рівні 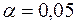 для статистичних даних задачі 2.1. передумова 2 виконується. ¥
для статистичних даних задачі 2.1. передумова 2 виконується. ¥
3.3. Тест рангової кореляції Спірмена і тест Голдфелда-Квандта дозволяють лише виявити наявність гетероскедастичності, але вони не дають можливості з’ясувати кількісний характер залежності дисперсій помилок регресії від значень незалежної змінної, і, отже, не дають методів усунення гетероскедастичності.
Для досягнення цієї мети необхідні деякі додаткові припущення стосовно характеру гетероскедастичності. Справді, без цих припущень, очевидно, неможливо було б оцінити 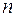 дисперсій помилок регресії
дисперсій помилок регресії 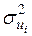 (
( 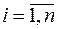 ) з допомогою
) з допомогою 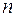 спостережень.
спостережень.
Найбільш простий і часто використовуваний тест на гетероскедастичність — тест Уайта. При його використанні припускається, що дисперсії помилок регресії є однією і тією ж функцією від спостережених значень незалежної змінної, тобто рівняння (3.10) набирають такого виду:
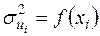 ,
, 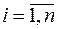 . (3.15)
. (3.15)
Найчастіше функція 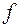 обирається квадратичною:
обирається квадратичною:
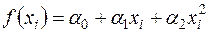 , (3.16)
, (3.16)
що відповідає тому, що 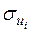 залежить від
залежить від 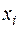 приблизно лінійно. У випадку гомоскедастичності
приблизно лінійно. У випадку гомоскедастичності 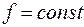 , тобто вибіркові коефіцієнти регресії
, тобто вибіркові коефіцієнти регресії 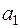 ,
, 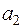 , які є оцінками невідомих чисел
, які є оцінками невідомих чисел 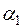 ,
, 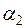 відповідно, незначуще відрізняються від нуля.
відповідно, незначуще відрізняються від нуля.
Ідея тесту Уайта полягає в оцінці функції 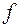 з (3.15) за допомогою відповідного рівняння регресії для квадратів залишків:
з (3.15) за допомогою відповідного рівняння регресії для квадратів залишків:
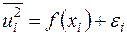 ,
, 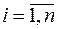 , (3.17)
, (3.17)
де 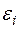 випадкова величина (за аналогією з
випадкова величина (за аналогією з 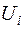 із рівняння (2.3)).
із рівняння (2.3)).
Відмітимо, що ліві частини рівнянь (3.15) та (3.17) співпадають, оскільки 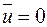 (див. 2.21)).
(див. 2.21)).
Гіпотеза про відсутність гетероскедастичності (умова 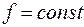 ) приймається у випадку незначущості регресії (3.17) в цілому (тобто одночасної незначущості теоретичних коефіцієнтів регресії
) приймається у випадку незначущості регресії (3.17) в цілому (тобто одночасної незначущості теоретичних коефіцієнтів регресії 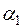 та
та 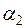 ).
).
Якщо обрати функцію 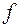 у вигляді (3.16), тоді знаходити «вручну» оцінки
у вигляді (3.16), тоді знаходити «вручну» оцінки 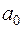 ,
, 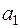 ,
, 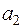 , а також їх середні квадратичні відхилення — достатньо працемісткий процес. Оптимальний шлях — використання персонального комп’ютера із відповідним програмним забезпеченням.
, а також їх середні квадратичні відхилення — достатньо працемісткий процес. Оптимальний шлях — використання персонального комп’ютера із відповідним програмним забезпеченням.
3.4. Тест Глейзера аналогічний тесту Уайта, тільки в якості залежної змінної для вивчення гетероскедастичності вибирається не квадрат залишків, а їх абсолютна величина, тобто розглядається регресія
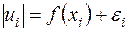 ,
, 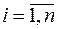 . (3.18)
. (3.18)
В якості функції 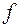 зазвичай обирається функція виду
зазвичай обирається функція виду
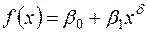 , (3.19)
, (3.19)
Регресія (3.18) вивчається при різних значеннях 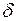 , а потім вибирається те конкретне значення, при якому коефіцієнт
, а потім вибирається те конкретне значення, при якому коефіцієнт 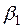 виявляється найбільш значущим, тобто має найбільше значення
виявляється найбільш значущим, тобто має найбільше значення 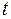 -статистики. При цьому в якості значень
-статистики. При цьому в якості значень 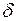 беруться числа: 1, 2, 3, 1/2, 1/3 тощо. Якщо ж
беруться числа: 1, 2, 3, 1/2, 1/3 тощо. Якщо ж 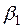 незначущий для всіх розглянутих значень
незначущий для всіх розглянутих значень 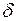 (випадок
(випадок 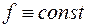 ), тоді робиться висновок про відсутність гетероскедастичності.
), тоді робиться висновок про відсутність гетероскедастичності.
Задача 3.4. На рівні значущості 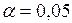 для задачі 2.1 перевірити виконання передумови 2 за тестом Глейзера.
для задачі 2.1 перевірити виконання передумови 2 за тестом Глейзера.
¡ Покладемо у функції (3.19) 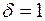 . Нехай
. Нехай 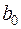 і
і 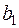 — оцінки невідомих параметрів
— оцінки невідомих параметрів 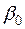 і
і 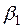 відповідно. Тоді оцінкою моделі (3.18) за статистичними даними
відповідно. Тоді оцінкою моделі (3.18) за статистичними даними 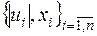 (
( 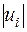 знайдені, а, отже, відомі) є
знайдені, а, отже, відомі) є 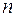 рівнянь
рівнянь
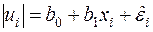 ,
, 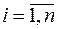 ,
,
де 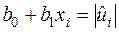 ,
, 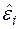 — вибіркова оцінка збурення
— вибіркова оцінка збурення 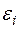 .
.
За формулами (2.12), (2.13) знайдемо МНК-оцінки 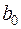 та
та 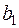 , використавши дані табл. 2.1 і 2.2:
, використавши дані табл. 2.1 і 2.2:
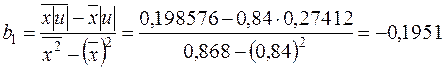 ,
,
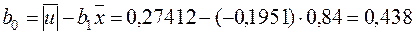 .
.
Незміщену точкову оцінку 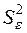 невідомої дисперсії збурень
невідомої дисперсії збурень 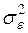 знайдемо за аналогом формули (2.22):
знайдемо за аналогом формули (2.22):
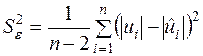 ,
,
попередньо обчисливши
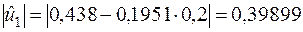 ,
,
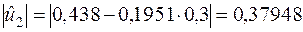 ,
,
… … … … … … … … … … … … …,
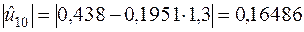 .
.
Отже, 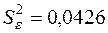 ,
, 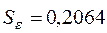 .
.
Для визначення значущості 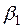 знайдемо
знайдемо 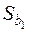 за формулою (2.30):
за формулою (2.30):
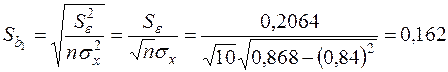 .
.
Тоді 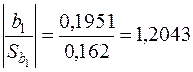 .
.
Але оскільки 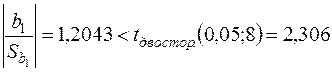 , то на рівні
, то на рівні 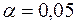 робимо висновок, що
робимо висновок, що 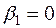 . Таким чином, у випадку
. Таким чином, у випадку 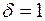
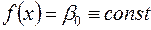 .
.
При розгляді випадків 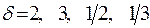 доцільно досліджувати рівняння
доцільно досліджувати рівняння
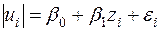 ,
, 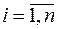 ,
,
де 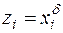 , за вище розглянутою схемою. Відповідні чисельні розрахунки для цих випадків наведені в §5.
, за вище розглянутою схемою. Відповідні чисельні розрахунки для цих випадків наведені в §5.
Виявляється, що і в цих випадках коефіцієнт регресії 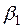 незначущий, тобто для статистичних даних задачі 2.1 передумова 2 виконується. ¥
незначущий, тобто для статистичних даних задачі 2.1 передумова 2 виконується. ¥
Зауваження. Припустимо, що значення 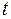 -статистики
-статистики 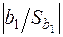 при
при 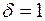 більше
більше 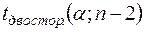 , що на рівні
, що на рівні 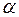 означає наявність гетероскедастичності. Тоді необхідно з’ясувати, який вид функції (3.19), тобто, якому значенню
означає наявність гетероскедастичності. Тоді необхідно з’ясувати, який вид функції (3.19), тобто, якому значенню 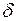 слід віддати перевагу. Для цього потрібно при різних значеннях
слід віддати перевагу. Для цього потрібно при різних значеннях 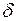 обчислити значення
обчислити значення 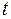 -статистики або значення коефіцієнта детермінації. Знайдене максимальне значення і відповідатиме шуканому значенню
-статистики або значення коефіцієнта детермінації. Знайдене максимальне значення і відповідатиме шуканому значенню 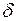 .
.
3.5. Повернемося до моделі (2.3)
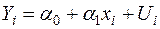 ,
, 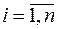 , (3.20)
, (3.20)
для якої встановлено існування гетероскедастичності, а за припущенням збурення 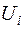 не корелюють між собою (
не корелюють між собою ( 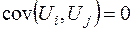
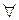
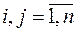 ,
, 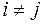 ). Поділимо ліву і праву частину рівнянь (3.20) на
). Поділимо ліву і праву частину рівнянь (3.20) на 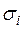 , де
, де 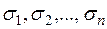 є фіксованими додатними числами, не рівними між собою. Тоді для моделі
є фіксованими додатними числами, не рівними між собою. Тоді для моделі
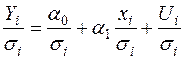 ,
, 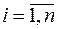 , (3.21)
, (3.21)
вже виконується умова гомоскедастичності, оскільки при 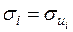
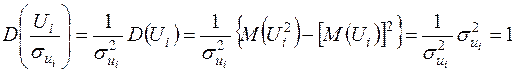 .
.
Нехай 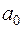 і
і 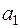 — оцінки невідомих параметрів
— оцінки невідомих параметрів 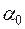 і
і 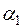 відповідно. Тоді оцінкою моделі (3.21) по вибірці
відповідно. Тоді оцінкою моделі (3.21) по вибірці 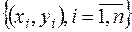 є
є 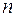 рівнянь
рівнянь
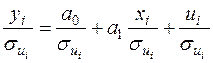 ,
, 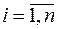 .
.
Оцінки 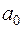 ,
, 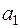 знайдемо із умови мінімізації функції
знайдемо із умови мінімізації функції
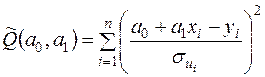 .
.
За аналогією із п.2 §2 отримаємо систему нормальних рівнянь
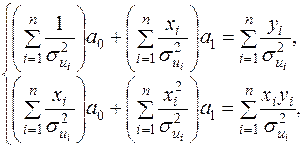 (3.22)
(3.22)
яка однозначно визначає невідомі оцінки 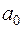 ,
, 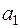 .
.
Описаний метод знаходження оцінок параметрів регресії називається методом зважених найменших квадратів (МЗНК). Можна безпосередньо перевірити, що МЗНК покращує точність моделі: оцінки коефіцієнтів для моделі (3.21) (її називають зваженою регресією) більш ефективні в порівнянні з оцінками звичайної регресії (3.20).
Для практичної реалізації МЗНК потрібно в системі рівнянь (3.22) замість 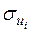 підставити знайдені за допомогою теста Глейзера значення
підставити знайдені за допомогою теста Глейзера значення 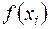 , які є статистичними оцінками невідомих
, які є статистичними оцінками невідомих 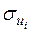 .
.
Зауваження. На практиці процедура усунення гетероскедастичності може викликати технічні труднощі. Справа в тому, що внаслідок використання оцінок 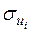 модель (3.21) не обов’язково виявиться гомоскедастичною з огляду на такі причини. По-перше, далеко не завжди виявляється правильним саме припущення (3.16) або (3.18). По-друге, функція
модель (3.21) не обов’язково виявиться гомоскедастичною з огляду на такі причини. По-перше, далеко не завжди виявляється правильним саме припущення (3.16) або (3.18). По-друге, функція 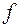 у формулі (3.15), взагалі кажучи, не обов’язково степенева (і, тим більше, не обов’язково квадратична), і у цьому випадку її підбір може виявитися далеко не таким простим.
у формулі (3.15), взагалі кажучи, не обов’язково степенева (і, тим більше, не обов’язково квадратична), і у цьому випадку її підбір може виявитися далеко не таким простим.
Другим недоліком тестів Уайта і Глейзера є те, що факт не виявлення ними гетероскедастичності, взагалі кажучи, не означає її відсутності. Справді, приймаючи гіпотезу 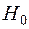 , ми приймаємо лише той факт, що відсутня певного виду залежність дисперсій помилок регресії від незалежної змінної.
, ми приймаємо лише той факт, що відсутня певного виду залежність дисперсій помилок регресії від незалежної змінної.
4. Передумова 3 передбачає відсутність кореляції між збуреннями 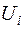 та
та 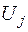 при
при 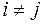 , тобто
, тобто 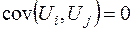
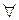
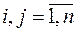 ,
, 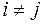 . Моделі, для яких не виконується ця передумова, називаються моделями із наявністю автокореляції.
. Моделі, для яких не виконується ця передумова, називаються моделями із наявністю автокореляції.
Відмітимо, що у випадку просторової вибірки відсутність автокореляції постулюється. Разом з тим при використанні комп’ютерних регресійних пакетів (незалежно від виду вибірки) наводиться значення статистики Дарбіна-Уотсона стосовно наявності автокореляції між сусідніми членами вибірки.
Для часових рядів модель (2.3) запишеться у такому вигляді:
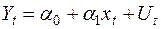 ,
, 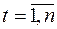 . (3.23)
. (3.23)
Якщо збурення 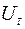 в різні моменти часу
в різні моменти часу 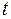 корелюють між собою, тоді між значеннями збурення існує залежність, яку у загальному випадку можна записати у вигляді
корелюють між собою, тоді між значеннями збурення існує залежність, яку у загальному випадку можна записати у вигляді
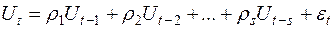 ,
, 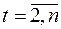 , (3.24)
, (3.24)
де 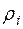 —
— 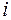 -тий коефіцієнт кореляції,
-тий коефіцієнт кореляції, 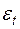 — випадкова величина,
— випадкова величина, 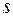 — величина запізнення.
— величина запізнення.
При виконанні співвідношення (3.24) із 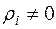 ,
, 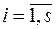 , говорять, що послідовність
, говорять, що послідовність 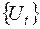
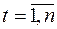 утворить авторегресійний процес
утворить авторегресійний процес 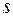 -го порядку. Назва «авторегресійний» зумовлена тим, що
-го порядку. Назва «авторегресійний» зумовлена тим, що 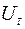 визначається значеннями цієї ж самої величини в попередніх моментах часу (запізненнями).
визначається значеннями цієї ж самої величини в попередніх моментах часу (запізненнями).
МНК при наявності корельованості збурень регресії дає незміщені і спроможні оцінки коефіцієнтів регресії, але вони вже є неефективними. Більше того, оцінки їх дисперсій неспроможні і зміщені (як правило, у бік заниження), тобто результати тестування гіпотез виявляються недостовірними.
Таким чином, актуальними є такі питання:
1) як діагностувати наявність автокореляції?
2) яким чином модель із автокореляцією можна було б привести до класичної регресійної моделі?
Відповідь на друге питання пов’язана з необхідністю розгляду узагальненого методу найменших квадратів (УМНК), який буде викладено пізніше.
5. Якщо в моделі (3.23) присутня автокореляція, тоді, як правило, найбільший вплив на наступне спостереження виявляє результат попереднього спостереження. Наприклад, коли розглядається ряд значень курсу деякої акції, то, очевидно, саме результат останніх торгів слугує відправною точкою для формування курсу на наступних торгах.
Ситуація, коли на значення спостереження 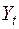 виявляє основний вплив не результат
виявляє основний вплив не результат 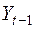 , а більш ранні значення, є достатньо рідкісною.
, а більш ранні значення, є достатньо рідкісною.
Таким чином, відсутність кореляції між сусідніми членами служить достатньою підставою вважати, що кореляція відсутня в цілому, і звичайний МНК дає адекватні і ефективні результати.
Тест Дарбіна-Уотсона визначає наявність автокореляції між сусідніми членами (часового) ряду. Він ґрунтується на простій ідеї: якщо кореляція збурень (залишків) регресії 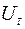 існує, то вона присутня у залишках регресії
існує, то вона присутня у залишках регресії 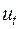 , які отримуються в результаті використання звичайного МНК. У тесті Дарбіна-Уотсона для оцінки кореляції використовується статистика виду
, які отримуються в результаті використання звичайного МНК. У тесті Дарбіна-Уотсона для оцінки кореляції використовується статистика виду
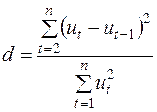 . (3.25)
. (3.25)
Можна довести, що статистика Дарбіна-Уотсона пов’язана з вибірковим коефіцієнтом кореляції між сусідніми спостереженнями таким чином:
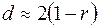 .
.
Природно, що у випадку відсутності автокореляції вибірковий коефіцієнт кореляції 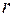 є близьким до нуля, а значення статистики
є близьким до нуля, а значення статистики 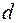 буде близьким до двох.
буде близьким до двох.
Якщо спостережене значення 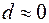 , то
, то 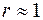 , тобто спостерігається додатна автокореляція, а якщо
, тобто спостерігається додатна автокореляція, а якщо 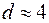 , то
, то 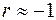 , тобто наявна від’ємна кореляція. У зв’язку з цим бажано мати відповідні порогові (критичні) значення, присутні у статистичних критеріях, і які або дозволяють прийняти гіпотезу, або примушують її відкинути. Проте, на жаль, такі критичні або порогові значення однозначно вказати неможливо.
, тобто наявна від’ємна кореляція. У зв’язку з цим бажано мати відповідні порогові (критичні) значення, присутні у статистичних критеріях, і які або дозволяють прийняти гіпотезу, або примушують її відкинути. Проте, на жаль, такі критичні або порогові значення однозначно вказати неможливо.
Тест Дарбіна-Уотсона має один суттєвий недолік — розподіл статистики 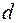 залежить не тільки від числа спостережень
залежить не тільки від числа спостережень 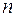 , але і від значень незалежної змінної
, але і від значень незалежної змінної 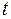 . Це означає, що тест Дарбіна-Уотсона, взагалі кажучи, не можна віднести до статистичних критеріїв, оскільки не можна вказати критичну область, яка дозволяла б відкинути гіпотезу про відсутність кореляції, якби виявилося, що в цю область потрапило б спостережене значення статистики
. Це означає, що тест Дарбіна-Уотсона, взагалі кажучи, не можна віднести до статистичних критеріїв, оскільки не можна вказати критичну область, яка дозволяла б відкинути гіпотезу про відсутність кореляції, якби виявилося, що в цю область потрапило б спостережене значення статистики 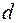 .
.
Проте існують два порогові значення 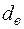 і
і 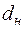 , які залежать тільки від
, які залежать тільки від 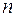 і рівня значущості, і такі, що виконуються наступні твердження.
і рівня значущості, і такі, що виконуються наступні твердження.
Якщо спостережене значення 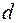 :
:
а) 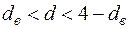 , то гіпотеза про відсутність автокореляції приймається;
, то гіпотеза про відсутність автокореляції приймається;
б) 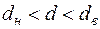 або
або 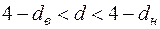 , то питання про відхилення або прийняття гіпотези залишається відкритим (значення
, то питання про відхилення або прийняття гіпотези залишається відкритим (значення 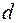 потрапляє у область невизначеності критерія);
потрапляє у область невизначеності критерія);
в) 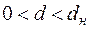 , то приймається альтернативна гіпотеза про додатну автокореляцію;
, то приймається альтернативна гіпотеза про додатну автокореляцію;
г) 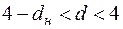 , то приймається альтернативна гіпотеза про від’ємну автокореляцію.
, то приймається альтернативна гіпотеза про від’ємну автокореляцію.
 Зобразимо наведені результати графічно:
Зобразимо наведені результати графічно:
Для 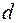 -статистики знайдені верхня
-статистики знайдені верхня 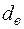 і нижня
і нижня 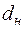 межі на рівнях значущості
межі на рівнях значущості 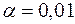 ;
; 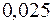 і
і 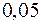 .
.
У табл. 5 додатків наведені значення статистик 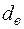 і
і 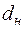 критерія Дарбіна-Уотсона для рівня значущості
критерія Дарбіна-Уотсона для рівня значущості 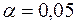 .
.
Недоліком критерія Дарбіна-Уотсона є наявність зон невизначеності цього критерія, а також те, що критичні значення 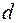 -статистики визначені для обсягів вибірки
-статистики визначені для обсягів вибірки 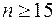 . Тим не менше, тест Дарбіна-Уотсона є найбільш використовуваним.
. Тим не менше, тест Дарбіна-Уотсона є найбільш використовуваним.
При використанні комп’ютерних регресійних пакетів значення статистики 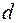 наводиться автоматично при оцінюванні моделі методом найменших квадратів.
наводиться автоматично при оцінюванні моделі методом найменших квадратів.
Задача 3.5. На рівні значущості 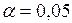 для задачі 2.1 перевірити виконання передумови 3 за тестом Дарбіна-Уотсона.
для задачі 2.1 перевірити виконання передумови 3 за тестом Дарбіна-Уотсона.
¡ Підсумок останнього рядка табл. 2.2 визначає знаменник дробу (3.25):
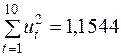 . Для обчислення чисельника цього ж дробу використаємо дані передостаннього рядка табл. 2.2:
. Для обчислення чисельника цього ж дробу використаємо дані передостаннього рядка табл. 2.2:
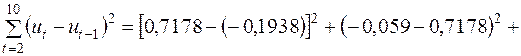
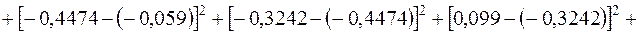
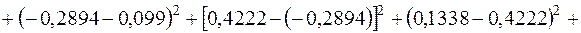
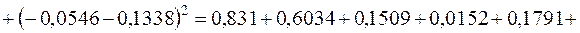
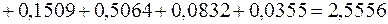 .
.
Спостережене значення статистики (3.25):
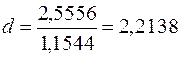 .
.
За табл. 5 додатків при 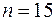 критичні значення
критичні значення 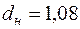 ,
, 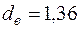 , тобто
, тобто 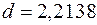 знаходиться в межах від
знаходиться в межах від 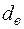 до
до 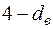 (
( 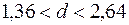 ). Як було відмічено вище, при
). Як було відмічено вище, при 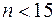 критичних значень
критичних значень 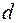 -статистики в таблиці немає, проте згідно з тенденцією їх змін із зменшенням
-статистики в таблиці немає, проте згідно з тенденцією їх змін із зменшенням 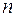 , можна припустити, що знайдене значення залишиться в інтервалі
, можна припустити, що знайдене значення залишиться в інтервалі 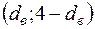 , тобто для статистичних даних задачі 2.1 на рівні значущості
, тобто для статистичних даних задачі 2.1 на рівні значущості 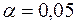 гіпотеза про відсутність автокореляції збурень не відхиляється (приймається). ¥
гіпотеза про відсутність автокореляції збурень не відхиляється (приймається). ¥
6. Статистика Дарбіна-Уотсона є найбільш важливим індикатором наявності автокореляції. Проте недоліками цієї статистики, окрім наявності зон невизначеності, є також обмеженість результату, яка полягає у тому, що кореляція виявляється тільки між сусідніми членами. Ця обставина приводить до необхідності використання інших тестів на наявність автокореляції. У всіх цих тестах в якості основної гіпотези 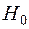 розглядається гіпотеза про відсутність автокореляції.
розглядається гіпотеза про відсутність автокореляції.
Тест серій (Бреуша-Годфрі) ґрунтується на такій ідеї: якщо існує кореляція між сусідніми спостереженнями, то природно очікувати, що у рівнянні
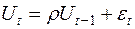 ,
, 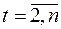 (3.26)
(3.26)
коефіцієнт 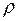 виявиться значуще відмінним від нуля. Відмітимо, що рівняння (3.26) є частковим видом рівняння (3.24) при
виявиться значуще відмінним від нуля. Відмітимо, що рівняння (3.26) є частковим видом рівняння (3.24) при 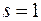 .
.
Практичне використання тесту серій полягає в оцінюванні методом найменших квадратів моделі (3.26).
Припустимо, що випадкова величина 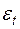 задовольняє передумовам 1-4. Порівняння моделей (3.26) і (2.3) дозволяє зробити висновок, що
задовольняє передумовам 1-4. Порівняння моделей (3.26) і (2.3) дозволяє зробити висновок, що 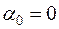 ,
, 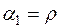 . Крім цього, вибіркою обсягом
. Крім цього, вибіркою обсягом 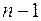 є дані
є дані
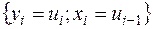 ,
, 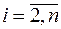 . (3.27)
. (3.27)
Тоді згідно з МНК із другого рівняння (2.12), де 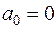 , отримаємо оцінку параметра
, отримаємо оцінку параметра 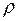 :
:
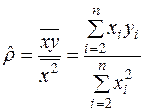 (3.28)
(3.28)
або із врахуванням (3.27)
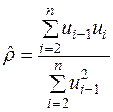 . (3.28*)
. (3.28*)
За аналогією із формулою (2.22) незміщеною оцінкою дисперсії збурень 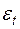 є
є
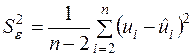 , (3.29)
, (3.29)
де 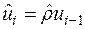 , а величина знаменника зумовлена тим, що обсяг вибірки
, а величина знаменника зумовлена тим, що обсяг вибірки 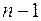 і число оцінюваних параметрів дорівнює 1.
і число оцінюваних параметрів дорівнює 1.
Із (3.28) та (3.27) отримаємо з урахуванням передумов 2, 3 та детермінованості 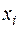 і
і 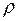
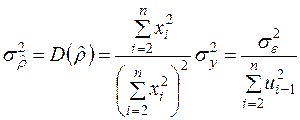 .
.
Незміщена оцінка 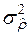 із врахуванням (3.29) має такий вигляд:
із врахуванням (3.29) має такий вигляд:
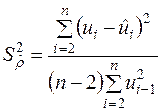 , (3.30)
, (3.30)
Зміст основної гіпотези Дата добавления: 2016-06-13; просмотров: 1872;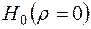 та альтернативної
та альтернативної 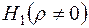 дозволяє сформулювати двосторонній критерій значущості оцінки
дозволяє сформулювати двосторонній критерій значущості оцінки
