Ошибки аппроксимации

Практически всегда фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим, тем лучше подобрано уравнение регрессии. Величина отклонений фактических и расчетных значений результативного признака 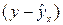по каждому наблюдению представляет собой ошибку аппроксимации. Число ошибок соответствует размеру совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю (когда в одном наблюдении фактическое и теоретическое значения результата совпадают).

Отклонения 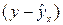несравнимы между собой, исключая величину, равную нулю. Отклонения 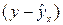можно рассматривать как абсолютную ошибку аппроксимации.

Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.

Поскольку 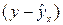может быть как величиной положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю:

.

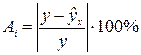Эти ошибки уже поддаются сравнению, но они оценивают каждое наблюдение в отдельности. Такую ошибку принято называть относительной ошибкой аппроксимации.

Чтобы оценить качество модели в целом, можно определить среднюю ошибку аппроксимации, представляющую собой среднюю арифметическую относительных ошибок аппроксимации по всем наблюдениям, включаемым в модель:

.

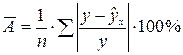Модель считается подобранной достаточно хорошо, если средняя ошибка аппроксимации не превышает 8–10%. Предпочтение отдается модели с наименьшей ошибкой .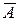

Возможно и другое определение средней ошибки аппроксимации:

.

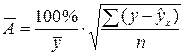Значения ошибок, рассчитанных по разным формулам будут отличаться друг от друга. Наиболее часто используется первый вариант расчета средней ошибки аппроксимации.