Сопряженное преобразование. Свойства.

Пусть e₁,…,e_n базис V, 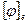- матрица линейного преобразования 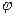, G_e – матрица Грама скалярного произведения. Перейдем от равенства векторов 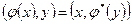к равенству координат 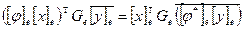. Из этого равенства выводим 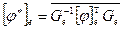. В случае ортонормированного базиса формула принимает более простой вид 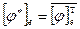. Для евклидова пространства, знак комплексного сопряжения можно опустить.

Свойство 8.3. Перечислим свойства сопряженного преобразования

1)

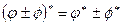
2)

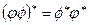
3)

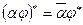
4)

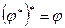
5) Если W инвариантное подпространство 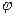, то ортогональное дополнение к W инвариантно относительно .

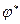Доказательство. Из равенства 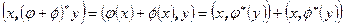выводим первое свойство. Второе свойство получается из равенств 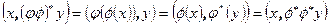. Для доказательства третьего свойства достаточно рассмотреть равенства 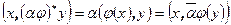. Четвертое свойство доказывается равенствами 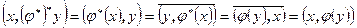. Докажем пятое свойство. Для произвольного вектора x из W и произвольного вектора 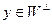скалярное произведение 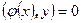. По определению сопряженного преобразования 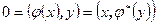, и, значит 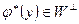, что и требовалось доказать.

Пятое свойство позволяет дать другое доказательство теоремы Шура.