Представление булевой функции формулой логики высказываний
Булевы функции.
DEF. Булевой функцией f(  ,
,  ,…,
,…, 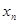 ) называется произвольная функция от п-переменных, отображающая множество {0;1} на это же самое множество {0;1}.
) называется произвольная функция от п-переменных, отображающая множество {0;1} на это же самое множество {0;1}.
Таким образом, все аргументы булевой функции (Б.ф.) принимают значения из множества {0;1} и сама функция принимает значения из этого же множества.
Всякую булеву функцию можно задать таблицей. Если f зависит от n переменных в таблице будет 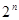 строк, в каждой из которых записан один из возможных наборов списка переменных.
строк, в каждой из которых записан один из возможных наборов списка переменных.
Пример: Если f(x) , то n=1; 21=2 строки в таблице;
Если f(x1,x2) , то n=2; 22=4 строки в таблице;
Если f(x1,x2,x3) , то n=3; 23=8 строки в таблице и т.д.
Например, для случая n=2 булеву функцию можно задать таблицей:
| x1 | x2 | f(x1, x2) |
Т.е. f(0,0)=f(1,1)=1 и f(0,1)=f(1,0)=0.
Если булева функция содержит n переменных, то различных наборов переменных будет 2n, а различных функций 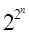 .
.
Пример: Если f(x), то n=1. Тогда 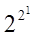 = 4 различных булевых функций:
= 4 различных булевых функций:
| x | f1 | f2 | f3 | f4 |
| 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| Б.ф. | 0 | 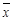
| 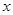
| 1 |
Очевидно, что каждой формуле логики высказываний можно поставить в соответствие булеву функцию, причем если формуле 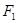 соответствует функция
соответствует функция 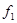 , а
, а 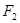 соответствует функция
соответствует функция 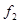 и при этом
и при этом 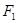 и
и 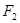 тождественно равны (
тождественно равны ( 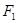 ≡
≡ 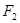 ), то
), то 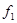 =
= 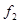 .
.
Докажем, что формулы алгебры логики дают все булевы функции. Для этого сформулируем:
DEF. 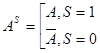 ,
,
(т.е. при 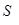 = 1 под
= 1 под 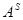 будем подразумевать формулу
будем подразумевать формулу 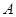 , а при
, а при 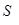 = 0 – формулу
= 0 – формулу 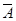 ).
).
При этом с каждым набором переменных < 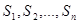 > будем ассоциировать элементарную конъюнкцию
> будем ассоциировать элементарную конъюнкцию 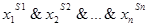 .
.
Лемма: Конъюнкция 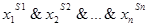 , ассоциированная с набором <
, ассоциированная с набором < 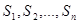 > обращается в единицу на одном и только одном наборе переменных <
> обращается в единицу на одном и только одном наборе переменных <  ,
,  ,…,
,…, 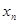 >, а именно на наборе <
>, а именно на наборе < 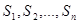 >.
>.
Доказательство:
В самом деле, элементарная конъюнкция 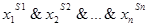 принимает значение единицы на наборе <
принимает значение единицы на наборе < 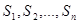 >, так как каждый её конъюнктивный член принимает значение единицы.
>, так как каждый её конъюнктивный член принимает значение единицы.
Действительно, возможны два случая:
1) если 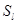 =1, то
=1, то 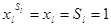 ;
;
2) если 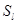 = 0, то
= 0, то 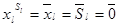 = 1, где l =1, 2, …, n.
= 1, где l =1, 2, …, n.
Таким образом, в каждом из этих случаев конъюнктивный член 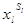 =1, но т.к. l- произвольное значение, тоэлементарная конъюнкция
=1, но т.к. l- произвольное значение, тоэлементарная конъюнкция 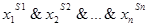 принимает значение единицы на наборе <
принимает значение единицы на наборе < 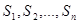 >.
>.
С другой стороны, пусть некоторый набор < 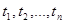 > не совпадает с набором <
> не совпадает с набором < 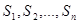 >, следовательно, при некотором номере l :
>, следовательно, при некотором номере l : 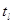 ¹
¹ 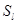 .
.
Здесь также возможны два случая:
1) 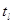 =1,
=1, 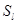 = 0;
= 0;
2) 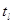 =0,
=0, 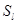 = 1.
= 1.
В первом случае: 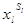 =
= 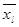 =
= 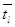 =
= 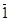 = 0; во втором случае
= 0; во втором случае 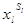 =
= 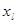 =
= 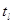 =0. Тогда в любом из этих случаев на наборе <
=0. Тогда в любом из этих случаев на наборе < 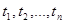 > конъюнктивный член
> конъюнктивный член 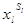 =0. А значит, элементарная конъюнкция
=0. А значит, элементарная конъюнкция 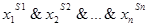 принимает значение 0 на этом наборе.
принимает значение 0 на этом наборе.
Лемма доказана.
Th: Пусть f(  ,
,  ,…,
,…, 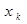 ) – булева функция от k переменных, где k ³ 1. Если функция f не равна тождественно нулю, то существует такая формула F, зависящая от списка переменных <
) – булева функция от k переменных, где k ³ 1. Если функция f не равна тождественно нулю, то существует такая формула F, зависящая от списка переменных <  ,
,  ,…,
,…, 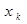 > и находящаяся с совершенной дизъюнктивной нормальной форме, что формула F выражает собой функцию f(
> и находящаяся с совершенной дизъюнктивной нормальной форме, что формула F выражает собой функцию f(  ,
,  ,…,
,…, 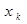 ). Формула F определена однозначно с точностью до порядка дизъюнктивных членов.
). Формула F определена однозначно с точностью до порядка дизъюнктивных членов.
Доказательство:
Существование
Пусть функция f(  ,
,  ,…,
,…, 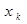 ) задана с помощью таблицы. Выберем в таблице все строки, соответствующие наборам, на которых функция f принимает значение истины. Такие строки существуют, так как по условию функция не равна тождественно нулю. Для каждого такого набора построим ассоциированную с ним элементарную конъюнкцию и составим дизъюнкцию таких конъюнкций. Полученная таким образом формула и будет искомой. Для подтверждения этого необходимо доказать два утверждения:
) задана с помощью таблицы. Выберем в таблице все строки, соответствующие наборам, на которых функция f принимает значение истины. Такие строки существуют, так как по условию функция не равна тождественно нулю. Для каждого такого набора построим ассоциированную с ним элементарную конъюнкцию и составим дизъюнкцию таких конъюнкций. Полученная таким образом формула и будет искомой. Для подтверждения этого необходимо доказать два утверждения:
1) f ( 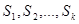 ) = 1, то и F=1 на этом наборе;
) = 1, то и F=1 на этом наборе;
2) f ( 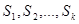 ) = 0, то и F=0 на этом наборе.
) = 0, то и F=0 на этом наборе.
Итак:
1) Пусть на некотором наборе < 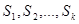 > функция f равна 1, тогда в таблице соответствующая строка находится среди выбранных, а значит, элементарная конъюнкция
> функция f равна 1, тогда в таблице соответствующая строка находится среди выбранных, а значит, элементарная конъюнкция 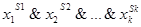 находится среди дизъюнктивных членов. По лемме данная конъюнкция принимает значение 1, а, следовательно, вся формула F равна 1 на этом наборе.
находится среди дизъюнктивных членов. По лемме данная конъюнкция принимает значение 1, а, следовательно, вся формула F равна 1 на этом наборе.
2) Пусть на некотором наборе < 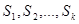 > функция f равна 0. Любой дизъюнктивный член формулы F имеет вид
> функция f равна 0. Любой дизъюнктивный член формулы F имеет вид 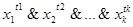 , причем набор <
, причем набор < 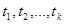 >отличен от набора <
>отличен от набора < 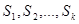 >, так как строка, соответствующая набору <
>, так как строка, соответствующая набору < 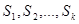 > не могла быть выбрана. По лемме каждая такая конъюнкция обращается в 0, а, следовательно, и вся формула F будет равна 0.
> не могла быть выбрана. По лемме каждая такая конъюнкция обращается в 0, а, следовательно, и вся формула F будет равна 0.
Единственность
Предположим противное: Пусть 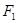 и
и 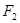 - две формулы, находящиеся в совершенной дизъюнктивной нормальной форме и выражающие функцию f, причем
- две формулы, находящиеся в совершенной дизъюнктивной нормальной форме и выражающие функцию f, причем 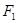 ¹
¹ 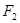 . Тогда либо в формуле
. Тогда либо в формуле 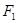 есть элементарная конъюнкция, не содержащаяся в
есть элементарная конъюнкция, не содержащаяся в 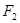 , либо в формуле
, либо в формуле 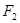 есть элементарная конъюнкция, не содержащаяся в
есть элементарная конъюнкция, не содержащаяся в 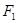 . Рассмотрим первый случай:
. Рассмотрим первый случай:
Если 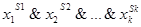 - элементарная конъюнкция, содержащаяся в
- элементарная конъюнкция, содержащаяся в 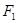 и не содержащаяся в
и не содержащаяся в 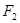 , то она будет ассоциирована с набором <
, то она будет ассоциирована с набором < 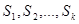 >. С одной стороны, т.к. она содержится в
>. С одной стороны, т.к. она содержится в 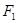 , то на данном наборе она принимает значение 1, а следовательно, и вся формула
, то на данном наборе она принимает значение 1, а следовательно, и вся формула 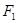 принимает значение 1. С другой стороны, любая элементарная конъюнкция, содержащаяся в
принимает значение 1. С другой стороны, любая элементарная конъюнкция, содержащаяся в 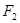 , будет ассоциирована с другим набором, значит, на этом наборе <
, будет ассоциирована с другим набором, значит, на этом наборе < 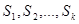 > будет принимать значение равное 0, а следовательно,
> будет принимать значение равное 0, а следовательно, 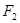 = 0. Тогда
= 0. Тогда 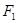 и
и 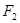 будут выражать собой различные булевы функции.
будут выражать собой различные булевы функции.
Таким образом, предположение о существовании двух формул неверно – единственность доказана.
Пример: Найти СДНФ.

| 
| 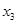
| f | |
| 1 | 1 | 1 | 1 | × |
| 1 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | × |
| 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | × |
| 0 | 0 | 1 | 0 | |
| 0 | 0 | 0 | 0 |
F = (  &
&  &
& 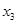 )Ú(
)Ú(  &
& 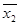 &
& 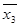 )Ú(
)Ú( 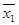 &
&  &
& 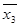 )
)
Замечания к теореме:
1. Из доказанной теоремы следует утверждение: для любой не тождественно ложной формулы А существует равносильная ей формула F, находящаяся в совершенной дизъюнктивной нормальной форме. Это утверждение было ранее доказано (формулу F получали с помощью равносильных преобразований). Таким образом, данная теорема дает второй способ получения совершенной дизъюнктивной нормальной формы.
2. Из доказанной теоремы следует утверждение об единственности совершенной дизъюнктивной нормальной формы для любой формулы А: если формула А выражает булеву функцию f, то и любая совершенная дизъюнктивная нормальная форма должна выражать собой ту же функцию, поэтому все совершенные дизъюнктивные нормальные формы должны совпадать с точностью до порядка элементарных конъюнкций.
Аналогично совершенной дизъюнктивной нормальной форме можно рассмотреть совершенную конъюнктивную нормальную форму и для нее справедлива следующая теорема:
Th: Пусть f(  ,
,  ,…,
,…, 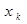 ) – булева функция от k переменных, где k ³ 1 и f не равна тождественно 1, тогда существует такая формула F, зависящая от списка переменных <
) – булева функция от k переменных, где k ³ 1 и f не равна тождественно 1, тогда существует такая формула F, зависящая от списка переменных <  ,
,  ,…,
,…, 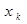 > и находящаяся с совершенной конъюнктивной нормальной форме, что формула F выражает собой функцию f(
> и находящаяся с совершенной конъюнктивной нормальной форме, что формула F выражает собой функцию f(  ,
,  ,…,
,…, 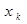 ). Формула F определена однозначно с точностью до порядка своих конъюнктивных членов.
). Формула F определена однозначно с точностью до порядка своих конъюнктивных членов.
Доказывается аналогично теореме о совершенной дизъюнктивной нормальной форме.
Пример: Найти СКНФ.

| 
| 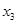
| f | |
| 1 | 1 | 1 | 1 | |
| 1 | 1 | 0 | 0 | × |
| 1 | 0 | 1 | 0 | × |
| 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 0 | × |
| 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 0 | × |
| 0 | 0 | 0 | 0 | × |
F = (x1\/x2\/x3)&( x1\/x2\/x3)&( x1\/x2\/x3)&( x1\/x2\/x3)&( x1\/x2\/x3)
Рассмотри все булевы функции от двух переменных.
Если n = 2,то 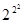 = 16различных булевых функций:
= 16различных булевых функций:

| 
| f1 | f2 | f3 | f4 | f5 | f6 | f7 | f8 | f9 |
| Булева функция |  & & 
|  & & 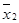
| 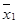 & & 
| 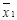 & & 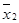
| 
| 
|  Û Û 
| 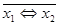
|

| 
| f10 | f11 | f12 | f13 | f14 | f15 | f16 |
| Булева функция | 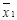
| 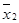
|  Ú Ú 
|  Ú Ú 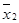
| 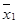 Ú Ú 
| 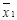 Ú Ú 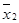
|
| <== предыдущая лекция | | | следующая лекция ==> |
| Защита окружающей местности от загрязнений поверхностными сточными водами. | | | ПРОИЗВОДСТВЕННОЕ ОСВЕЩЕНИЕ |
Дата добавления: 2016-05-16; просмотров: 2059;
