Постановка задачи интерполяции
Лекция 8
ОБРАБОТКА ДАННЫХ. ЧИСЛЕННЫЕ МЕТОДЫ ПРИБЛИЖЕНИЯ ФУНКЦИЙ. ИНТЕРПОЛЯЦИЯ
Содержание
· Области применения задачи приближения функций.
· Основные виды обработки данных: интерполяция, экстраполяция и аппроксимация.
· Постановка задачи интерполяции.
· Метод неопределенных коэффициентов
· Интерполяционный полином Лагранжа.
· Интерполяционный полином Ньютона.
· Погрешность полиномиальной интерполяции.
· Сплайн-интерполяция.
· Тригонометрическая интерполяция.
8.1. Области применения задачи приближения функций
В технологии обработки данных важное место занимают методы приближения функций более простыми, хорошо изученными функциями, методы численного дифференцирования и численного интегрирования. При этом исследуемая приближаемая функция может быть задана как в аналитическом, так и дискретном виде (в виде таблицы экспериментальных данных).
Подобные задачи (иначе интерполяция или аппроксимация функций) возникают в тех случаях, когда:
· функция задана в виде таблицы, и необходимо знать значения функции для промежуточных значений аргументов, расположенных в таблице между узлами xi, i = 0,…. n, а также для аргументов, расположенных вне таблицы;
· известно лишь табличное представление функции и требуется определить ее аналитическое выражение;
· известно аналитическое выражение функции, но оно имеет очень сложный вид, вследствие чего возникает необходимость представления этой функции в более простом виде. Например, при вычислении определенных интегралов вида
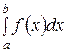
можно заменить подынтегральную функцию f(x) некоторой приближенной функцией P(x) в виде многочлена. Тогда
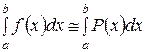 .
.
8.2. Основные виды обработки данных: интерполяция, экстраполяция и аппроксимация
Разберемся с рядом терминов, используемых в литературе при описании технологии приближения функций. Итак, пусть некоторая функция f(x)определена рядом своих узловых точек (xi, yi) на некотором отрезке [a, b]. Под интерполяцией мы будем подразумевать вычисление значений f(x) в любом промежутке [xi, xi+1] в пределах отрезка [a, b]. Соответственно, любое вычислениеf(x)вне отрезка [a, b] является экстраполяцией.
Наиболее распространены следующие виды интерполяции:
· линейная интерполяция, при которой промежуточные точки, расположенные между двумя узловыми точками (xi, yi) и (xi+1, yi+1), лежат на отрезке прямой, соединяющей две ближайшие узловые точки;
· квадратичная интерполяция, при которой промежуточные точки между узловыми точками (xi, yi), (xi+1, yi+1) и (xi+2, yi+2) лежат на отрезке параболы, соединяющей эти узловые точки;
· полиномиальная интерполяция, при которой промежуточные точки вычисляются как значение некоторого многочлена pn(x), имеющего значения в узловых точках точно совпадающие с fi(xi);
· сплайновая интерполяция, при которой промежуточные точки находятся с помощью отрезков полиномов невысокой степени, проходящих через узловые точки и поддерживающие определенные условия стыковки в концевых точках;
Подчеркнем ещё раз, что при интерполяции задача сводится к вычислению значений функции между узловыми точками (узлами), в то время как при экстраполяции — к вычислению функции вне того интервала, на котором она задана в виде таблицы, графически или иным способом.
При аппроксимации таблично заданная функция (что, кстати, не является обязательным признаком аппроксимации) заменяется другой функцией, как правило, более простой и поэтому более быстро вычисляемой. Последняя приближенно описывает поведение исходной функции на некотором отрезке. При этом на различных отрезках аппроксимирующие функции могут быть (и чаще всего бывают) разными.
Примечание. Для иллюстрации возможного использования процедуры аппроксимации можно привести задачу экстракции параметров моделей микроэлектронных приборов из экспериментальных данных.
Постановка задачи интерполяции
Пусть на отрезке xÎ[a, b] задана функция f(x), с помощью которой построена сеточная функция (табл. 8.1) или задана экспериментальная таблица (табл. 8.1).
Определение 1.Точки x0 , …, xn называются узлами интерполяции.
Требуется найти аналитическое выражение функции F(x), совпадающей в узлах интерполяции со значениями данной функции, т.е.
F(x0) = y0, F(x1) = y1, …, F(xn) = yn . (8.5)
Определение 2.Процесс вычисления значений функции F(x) в точках отличных от узлов интерполирования называется интерполированием функции f(x). Если xÎ[x0, xn], то задача вычисления приближенного значения функции в точке х называется интерполированием, иначе — экстраполированием.
Геометрически задача интерполирования функции одной переменной означает построение кривой, проходящей через заданные точки (x0, y0), (x1, y1), …, (xn, yn) (рис. 8.1).
8.3.1. Метод неопределенных коэффициентов
В рассмотренной постановке задача может иметь бесконечное число решений или не иметь ни одного решения. Однако эта задача становится однозначно разрешимой, если вместо произвольной функции F(x) искать полином Pn(x)
степени не выше n, удовлетворяющий условиям (8.5), т. е. такой, что в каждой узловой точке i выполняется условие:
Pn(xi)= f(xi) при i= 1, 2,…, n
При сглаживании функции (или экспериментальной таблицы) с помощью интерполяции в соответствии с условием интерполяции (8.2) значение интерполирующей функции и значение заданной функции в узлах сетки должны быть одинаковыми, следовательно, погрешность интерполяции в узлах xi, i = 0,…, n равна нулю (рис. 8.1).
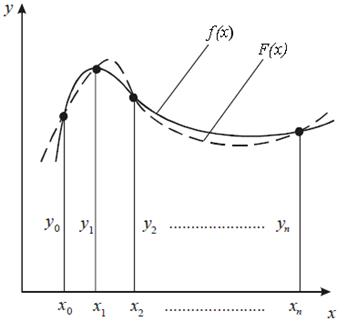
Рис. 8.1. Иллюстрация процедуры интерполяции
В общем случае задача интерполяции имеет не единственное решение, но в случае использования в качестве интерполирующей функции многочлена n-й степени (требующий n+1 узел интерполяции) задача интерполяция табличной функции вида (8.1) имеет единственное решение, т.е. коэффициенты a0,…, an (в количестве n+1) определяются единственным образом.
Действительно, используя табл. 8.1, можно составить систему из n+1 линейных уравнений (СЛАУ) относительно неизвестных коэффициентов a0,…, an:
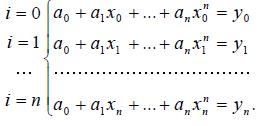 (8.6)
(8.6)
Матрица коэффициентов этой СЛАУ (8.6) носит специальное название — матрицы Вандермонда. Ее определитель не равен нулю, поскольку все значения узлов интерполяции различны между собой и ни одна из строк не является линейной комбинацией других строк, т.е.
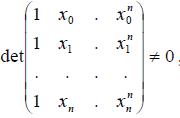 (8.7)
(8.7)
Таким образом, СЛАУ, а значит и задача полиномиальной интерполяции имеет единственное решение, поэтому вектор коэффициентов a0 ,…, an может быть выбран единственным образом.
Примечание. Отметим, что вычисление коэффициентов полинома посредством решения системы (8.6) в вычислительной практике реализуется крайне редко. Причиной этого является плохая обусловленность матрицы Вандермонда, приводящая к заметному росту погрешности при выполнении условий интерполирования уже при сравнительно невысоких порядках полинома. К этому следует добавить, что вычислительные затраты реализации метода пропорциональны n3.
Дата добавления: 2016-04-22; просмотров: 7194;
