МОСТОВОЙ МЕТОД ИЗМЕРЕНИЯ
Мостовые схемы широко применяются в лабораторной практике для измерения электрических характеристик (например, R, C, L) методом сравнения с аналогичными величинами, значения которых известны. Такой метод обладает многими достоинствами, в частности, можно достичь большой точности измерений без использования сложных и дорогостоящих приборов.
Мост Уитстона
Простейшим примером мостовой схемы может служить «мост Уитстона» – схема, впервые разработанная в 1844 г. Чарльзом Уитстоном (Charles Wheatstone, 1802-75) для измерения сопротивлений (рис. 24).
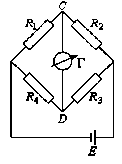
Рис. 24.
Рассмотрим принцип действия мостовой схемы на этом простом примере (рис. 24). Мост Уитстона включает в себя четыре резистора (R1, R2, R3, R4) – четыре плеча моста, соединенные четырехугольником, источник тока (Е), включенный в одну диагональ моста, и гальванометр (Г), включенный в другую диагональ. Одно из сопротивлений неизвестно, три другие известны и хотя бы одно из них может изменяться. Варьируя величину регулируемого сопротивления, можно добиться такого состояния схемы, при котором разность потенциалов между точками С и D равна 0. Индикатором служит гальванометр, показывающий в этом случае отсутствие тока в ветви CD. В таком состоянии мост называется сбалансированным. Очевидно, что в этом случае
I1 = I2, I3 = I4, I1·R1 = I4·R4, I2·R2 = I3·R3.
Решив эту систему уравнений, получаем:
R1·R3 = R4·R2 или 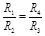 .
.
То есть если мост сбалансирован, то между сопротивлениями существует определенное соотношение и, следовательно, неизвестное сопротивление можно выразить через три другие.
Мосты переменного тока
Мостовые схемы можно применять и для измерения таких величин, как емкости (C) и индуктивности (L). Однако для этих целей уже необходимо использовать мосты переменного тока.
По аналогии с мостом Уитстона изобразим схему моста переменного тока (рис. 25).
Пусть в мост переменного тока входят четыре элемента (Z1, Z2, Z3, Z4), один из которых следует определить, а также источник питания (E) и измерительный прибор (V). При отсутствии тока в измерительном приборе мост будет сбалансирован. Так же как для моста Уитстона, в этом случае между импедансами (полными сопротивлениями) плеч моста имеет место соотношение, которое позволяет вычислить искомый импеданс одного из плеч по известным импедансам других плеч. Найдем это соотношение.
Баланс моста достигается только в том случае, когда потенциалы в точках C и D равны друг другу в любой момент времени. Это имеет место при равенстве падений напряжения (U1 и U4) на Z1 и Z4 как по амплитуде, так и по фазе. При балансе имеем
I1 = I2 = 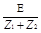 , I3 = I4 =
, I3 = I4 = 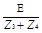 .
.
Выразим U1 и U4:
U1 = I1·Z1 = 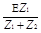 , U4 = I4·Z4 =
, U4 = I4·Z4 = 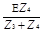 .
.
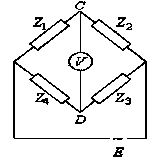
Рис. 25.
Так как U1 = U4, получаем соотношение для импедансов:
Z1·Z3 = Z4·Z2 или 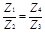 . .
| (51) |
Значения величин полных сопротивлений (импедансов) при математических действиях с ними обычно выражают комплексными числами[1]:
Z = R + i·X,
где R – активная составляющая полного сопротивления Z, X – реактивная составляющая полного сопротивления Z.
Тогда уравнение (51) примет вид:
| (R1 + i·X1)·(R3 + i·X3) = (R2 + i·X2)·(R4 + i·X4). | (52) |
Выполнение такого равенства возможно только при одновременном выполнении двух условий – равенстве действительных и мнимых частей, т.е. оно преобразуется в систему из двух уравнений:
| R1·R3 - X1·X3 = R2·R4 - X2·X4, | (53) |
| X1·R3 + X3·R1 = X2·R4 + X4·R2. | (54) |
Отсюда вытекает необходимость выполнения одновременно двух условий. Физический смысл этого требования заключается в том, что для баланса требуется совпадение переменных потенциалов в точках С и D по фазе и по амплитуде. Следовательно, для балансировки такого моста необходимо в общем случае регулировать как минимум два элемента. Также видно, что если импеданс искомого плеча включает в себя реактивную составляющую (C или L), то, по крайней мере, еще одно из плеч тоже должно включать таковую.
При работе с мостами следует иметь в виду, что принципиальная схема является идеализированной. Элементы схемы связаны между собой не только изображенными проводами, но и паразитными емкостями, а иногда и паразитными взаимоиндуктивностями; кроме того, реальные конденсаторы часто обладают «утечкой», т.е. их активное сопротивление не равно нулю. Эти причины, а также неидеальность приборов и т.п., приводят к тому, что на практике обычно невозможно добиться идеального баланса. При работе добиваются не отсутствия тока в ветви CD, а его минимума.
Лабораторная работа 44
ИЗМЕРЕНИЕ ЕМКОСТЕЙ КОНДЕНСАТОРОВ С ПОМОЩЬЮ МОСТА ПЕРЕМЕННОГО ТОКА
Задачи работы
1. Измерение величин нескольких емкостей.
2. Расчет емкостных сопротивлений.
Физическое обоснование эксперимента
Прежде чем приступать к выполнению работы, необходимо ознакомиться в данном учебном пособии с главой «Мостовой метод измерений».
Метод исследования и описание установки
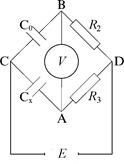
Рис. 44.1.
Экспериментальная установка представляет собой мостовую схему, изображенную на рис. 44.1. Здесь R3 и R2 – магазины сопротивлений. С0 – магазин емкостей, СX – конденсатор, емкость которого требуется определить. В качестве источника питания используется звуковой генератор ГЗ-34. В другую диагональ моста включен милливольтметр В3-39.
Как известно, конденсаторы обладают емкостным сопротивлением 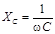 , где C – емкость, w = 2p·f – круговая частота (f – частота переменного тока). Полные сопротивления плеч такого моста представляют собой соответственно:
, где C – емкость, w = 2p·f – круговая частота (f – частота переменного тока). Полные сопротивления плеч такого моста представляют собой соответственно:
Z1 = X1 = 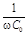
| (R1 = 0); |
| Z2 = R2 | (X2 = 0); |
| Z3 = R3 | (X3 = 0); |
Z4 = X4 = 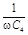
| (R4 = 0). |
Запишем применительно к такой схеме систему уравнений (53) и (54), которая должна выполняться при балансе моста. Видно, что уравнение (53) выполняется автоматически, так как R1 = 0, X2 = 0, X3 = 0, R4= 0. А уравнение (54) принимает вид
X1·R3 = X4·R2.
Подставив в него значения Х1 и Х2, получаем
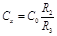 . .
| (44.1) |
Таким образом, если мост сбалансирован, то Сx можно определить, зная величины С0, R3 и R2.
Порядок выполнения работы
1. Собрать электрическую схему в соответствии с рис. 44.1, включив в нее один из исследуемых конденсаторов.
2. Установить на генераторе частоту 1000 Гц.
3. Установить на магазинах сопротивлений R3 и R2 по 500Ом.
4. Установить на магазине емкостей С0 = 0.
5. Установить предел измерений вольтметра 10 В.
6. Проверить электрическую схему.
7. Включить генератор и вольтметр (после проверки схемы лаборантом), дать приборам прогреться.
8. Изменяя величину емкости магазина емкостей С0, добиться минимального показания вольтметра. При этом, так как В3-39 – прибор многопредельный, то, по мере уменьшения его показаний, следует увеличивать его чувствительность (уменьшать пределы измерений).
9. Повторить балансировку, изменяя сопротивления R3 и R2 или частоту (по указанию преподавателя).
10. Провести аналогичные измерения для других неизвестных конденсаторов. Рассчитать их емкостные сопротивления.
11. В данной работе требуется определить, также, емкости и емкостные сопротивления некоторых (по указанию преподавателя) комбинаций конденсаторов при их параллельном и последовательном соединениях. Полученные значения сравнить со значениями, рассчитанными по формулам для данных комбинаций.
Содержание отчета
1. Схема установки.
2. Результаты всех измерений (желательно в виде таблицы).
3. Расчет значений емкостей и емкостных сопротивлений всех исследованных конденсаторов и их комбинаций.
4. Расчет теоретических значений емкостей исследованных комбинаций конденсаторов. Сравнение теоретических результатов с экспериментальными.
5. Расчеты погрешности измерений двумя способами: на основании класса точности приборов и, где возможно, учитывая разброс результатов измерений при варьировании сопротивлений.
6. Окончательные результаты с указанием погрешностей.
Контрольные вопросы
s От каких параметров зависит емкостное сопротивление?
s В чем принципиальное различие мостов постоянного и переменного тока?
s Каков сдвиг по фазе на емкости (индуктивности) между током и напряжением?
s В каком случае общая емкость (емкостное сопротивление) больше: при параллельном или при последовательном включении конденсаторов?
Лабораторная работа 45
ИЗМЕРЕНИЕ ИНДУКТИВНОСТЕЙ КАТУШЕК С ПОМОЩЬЮ МОСТА ПЕРЕМЕННОГО ТОКА
Задачи работы
1. Измерение величины индуктивностей нескольких катушек.
2. Расчет их активных и реактивных сопротивлений.
Физическое обоснование эксперимента
Прежде чем приступать к выполнению работы, необходимо ознакомиться в данном учебном пособии с главой «Мостовой метод измерений».
Метод исследования и описание установки
Экспериментальная установка представляет собой мостовую схему, изображенную на рис.45.1. Здесь R1, R2, R3 и R4 – магазины сопротивлений, L0 – эталонная катушка с известной индуктивностью L0и известным активным сопротивлением r0, LX – исследуемый соленоид, для которого требуется определить индуктивность LX и активное сопротивление rX. В качестве источника питания в одну из диагоналей моста включается либо звуковой генератор Гз, либо источник постоянного тока Е (переключение производится ключом К2). Ключ К служит для замыкания цепи гальванометра при измерении на постоянном токе.
В другую диагональ моста (CD) могут быть включены либо гальванометр Г (в случае измерений на постоянном токе), либо ламповый милливольтметр В3-39 (в случае измерений на переменном токе). Переключение производится ключом К1.
Как известно, сопротивление соленоида имеет активную и реактивную составляющие, и, в общем случае, равно:
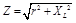 ,
,
где ХL = wL – индуктивное сопротивление, w = 2pf – круговая частота (f – частота переменного тока).
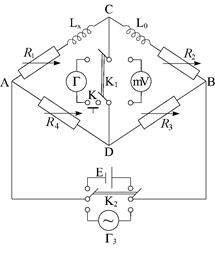
Рис. 45.1.
Или, используя способ записи с помощью комплексных чисел:
Z = r + i·w·L.
Полные сопротивления плеч такого моста представляют собой соответственно:
Z1 = R1 + rX + i·w·LX,
Z2 = R2 + r0 + i·w·L0,
Z3 = R3 (X3 = 0),
Z4 = R4 (X4 = 0).
Запишем, применительно к такой схеме, систему уравнений (53) и (54), которая должна выполняться при балансе моста. Так как X4 = 0 и X3 = 0, уравнения (53) и (54) принимают вид
| (R1 +rX)·R3 = (R2 + r0)·R4 , | (45.1) |
| LX·R3 = L0·R4. | (45.2) |
Перепишем получившуюся систему уравнений в более наглядном виде и проанализируем ее[2]:
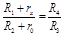 , ,
| (45.3) |
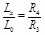 . .
| (45.4) |
Если в плечи моста, содержащие индуктивности, не включать дополнительные сопротивления (R1 = R2 = 0), то одновременное выполнение этих двух равенств в общем случае невозможно. Такое совпадение означало бы, что активные сопротивления катушек и их индуктивности находятся в одинаковом соотношении, что весьма маловероятно, так как активное сопротивление катушки и ее индуктивность определяются различными физическими причинами. Для балансировки рассматриваемого моста необходимо подключать дополнительные активные сопротивление R1 и R2 (или хотя бы одно из них). При этом выбор того плеча, в которое надо включать сопротивление, определяется соотношением между включенными в мост индуктивностями и их активными сопротивлениями.
Выполнение уравнений (45.3) и (45.4) соответствует балансу моста, т.е. отсутствию разности потенциалов между точками C и D в любой момент времени. Анализ уравнений показывает, что для достижения этого необходимо регулировать, как минимум, два параметра R1 и/или R2 и отношение R4/R3. Практически это довольно сложно в условиях, когда в плечах моста уже есть неизменные сопротивления (r0 + i·w·L0) и (rX + i·w·LX).
Кроме того, в диагонали моста CD возможно получение минимумов напряжения и не соответствующих состоянию баланса в случае, когда потенциалы в точках C и D не совпадают по фазе. Дополнительно затрудняет измерения то обстоятельство, что, и при условии выполнения уравнений (45.3) и (45.4) практически не достигается полное отсутствие тока, а только более «глубокий» минимум. Вспомогательное уравновешивание моста на постоянном токе позволяет проверить достижение состояния истинного баланса, а кроме того, упрощает поиски «истинного», наиболее глубокого минимума.
Отсутствие тока в диагонали CD при балансе на постоянном токе свидетельствует о выполнении уравнения (45.3). Если минимум сигнала в CD на переменном токе получен при том же отношении R4/R3, что и на постоянном токе, то это будет означать, что оба уравнения выполняются и баланс достигнут.
Используя полученные значения сопротивлений R1, R2, R3 и R4, можно из уравнения (45.3) вычислить значение активного сопротивления исследуемой катушки, а из уравнения (45.4) – значение ее индуктивности.
Порядок выполнения работы и обработка результатов измерений
1. Собрать электрическую схему в соответствии с рис. 45.1, включив в нее один из исследуемых соленоидов. На генераторе уже установлена частота, равная 1000 Гц.
2. Установить на магазинах сопротивлений: R1 = R2 = 0, R3 = R4 = 500 Ом.
3. Установить предел измерений вольтметра 30 В.
4. Перевести ключи К1 и К2 в положение «переменный ток». Включить генератор и вольтметр (после проверки схемы), дать приборам прогреться.
5. Провести первичную балансировку на переменном токе, т.е. изменяя величины сопротивлений R3 и R4, добиться минимального показания вольтметра. При этом, так как В3-39 – прибор многопредельный, то, по мере уменьшения его показаний, следует увеличивать его чувствительность (уменьшать пределы измерений). Записать получившиеся значения R3 и R4.
6. Переключить схему на постоянный ток (ключи К1 и К2 в положение «постоянный ток»). Изменяя R3 и R4, добиться баланса (отсутствия тока в гальванометре) при постоянном токе. При измерении замыкать ключ К. Вспомним рабочую систему уравнений, которые должны выполняться одновременно: (R1 + rX)/(R2 + r0) = R4/R3 и LX/L0 = R4/R3. Первое из этих уравнений выполняется и при балансе на постоянном токе, так как в него входят только чисто активные сопротивления. Сравним получившиеся в эксперименте отношения (R4/R3)пост и (R4/R3)перем. Чтобы оба уравнения выполнялись одновременно, необходимо изменить R1 или R2, а так как и R1, и R2 пока равны нулю, необходимо сделать одно из них отличным от нуля. В зависимости от соотношения между (R4/R3)пост и (R4/R3)перем, надо вводить или R1, или R2. Из системы уравнений видно, что для того, чтобы оба уравнения выполнялись при одном и том же отношении R4/R3, надо:
если (R4/R3)пост > (R4/R3)перем, то увеличить R2,
если (R4/R3)пост < (R4/R3)перем, то увеличить R1.
7. Восстановить на магазинах сопротивлений R3 и R4 значения, найденные при балансировке на переменном токе. И, изменяя R1 или R2 (в соответствии с выше сказанным), вновь добиться баланса на постоянном токе.
8. Переключить схему на переменный ток (ключи К1 и К2 в положение «переменный ток»). Изменяя R3 и R4, вновь добиться баланса на переменном токе.
9. Вновь переключить схему на постоянный ток (ключи К1 и К2 в положение «постоянный ток»). Изменяя R1 или R2, добиться баланса на постоянном токе.
10. Повторять операции 8 и 9 до тех пор, пока баланс не будет выполняться одновременно на постоянном и переменном токе (при одних и тех же значениях R1, R2, R3 и R4). Из уравнений (45.3) и (45.4), используя полученные значения величин R1, R2, R3 и R4, рассчитать величины LX и rX. Параметры эталонного соленоида: L0 = 1 Гн и r0 = 222,7 Ом.
11. Провести аналогичные измерения для других соленоидов (по указанию преподавателя). Рассчитать их индуктивности и активные сопротивления.
В данной работе рекомендуется определить также индуктивности и активные сопротивления некоторых (по указанию преподавателя) комбинаций соленоидов при их согласованном и бифилярном соединениях. В этом случае требуется дополнительно рассчитать коэффициенты взаимоиндукции М и связи К этих катушек из следующих формул (подробнее см. Лабораторную работу 42):
L = L1 + L2 ± 2M,
 .
.
Здесь знак «плюс» берется при согласованном, а «минус» – при бифилярном включении катушек.
Содержание отчета
1. Схема установки.
2. Результаты всех измерений в виде таблицы.
3. Расчет значений индуктивностей и активных сопротивлений всех исследованных соленоидов и их комбинаций.
4. Расчет индуктивностей и активных сопротивления комбинаций соленоидов при их согласованном и бифилярном соединениях, коэффициента взаимоиндукции и коэффициента связи (по указанию преподавателя).
5. Расчеты погрешностей измерений на основании класса точности приборов.
6. Окончательные результаты с указанием погрешностей.
Контрольные вопросы
s От каких параметров зависит индуктивное сопротивление?
s В чем принципиальное различие мостов постоянного и переменного тока?
s Каков сдвиг по фазе на емкости (индуктивности) между током и напряжением?
s В каком случае общая индуктивность больше: при согласованном или при бифилярном включении соленоидов?
[1] Между падениями напряжения на активном и реактивном сопротивлениях существует сдвиг по фазе на p/2. Полное сопротивление можно представить как векторную сумму активного и реактивного сопротивлений, аналогично тому, как представляют комплексные числа, состоящие из действительной и мнимой частей. Поэтому и математические операции с полными сопротивлениями можно производить как с комплексными числами, где активное сопротивление - вещественная часть числа, реактивное - мнимая.
[2] Заметим, что равенства выполняются автоматически при R4 = R3 = 0 и в процессе работы необходимо следить, чтобы R3 и R4 были отличны от нуля.
| <== предыдущая лекция | | | следующая лекция ==> |
| Среднеквадратичная погрешность среднего арифметического | | | Дослідження насосної функції серця |
Дата добавления: 2016-04-19; просмотров: 7373;
