Уравнение пьезопроводности

Уравнение неразрывности:

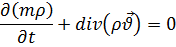
Закон Дарси:

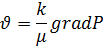
Уравнение состояния:

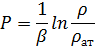
Путем синтеза данных трех уравнений выведено уравнение пьезопроводности:

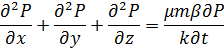
Или

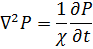
Уравнение пьезопроводности справедливо при следующих допущениях:

1. Процесс фильтрации и деформаций изотермический;

2. Режим пласта упругий, в пласте движется однородная ньютоновская жидкость по линейному закону фильтрации Дарси;

3. Пористая среда однородна и изотропна по проницаемости; предполагается, что при фильтрации отсутствует физико-химическое взаимодействие между пористой средой и флюидом;

4. Пористая среда и пластовый флюид упругие и их объемные деформации подчиняются линейному закону Гука, а именно, пористость и плотность жидкости линейно зависят от давления;

5. Силы инерции и гравитации не учитываются.

Для простейших одномерных фильтрационных потоков уравнение пьезопроводности может быть записано в виде:

где j=0; 1; 2 для ЛФП, РФП иСФП соответственно

Тема №2. Внутренние и внешние граничные условия

Внутренние граничные условия (на забое, на стенке скважины).

1. Скважина работает на установившемся режиме, с постоянным дебитом и, если фильтрация происходит по закону Дарси,

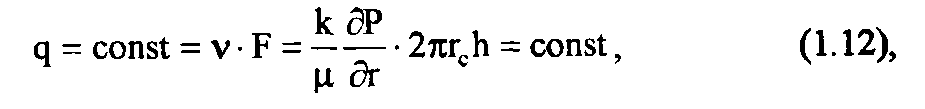
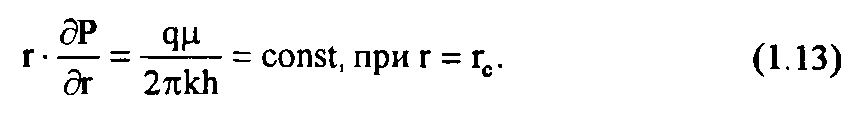
2. Скважина закрыта (отключена, не работает), q=0:

3. Скважина работает с постоянным давлением на забое:

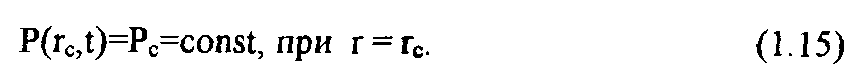
4. Скважина работает с заданным переменным забойным давлением:

5. Скважина работает с переменным дебитом на забое:

Возможны следующие из краевых условий, соответствующие физическим геолого-промысловым условиям залежи:

1. Модель «бесконечного» пласта (бесконечный по простиранию пласт):

где r —> ω.

2. Модель «замкнутого, закрытого» пласта, когда внешняя граница непроницаема и на границе q==0:

или

где n - нормаль к границе (непроницаемому сбросу, кровле, подошве пласта).

3. Модель «открытого пласта» с постоянным перетоком через границу, на контуре питания. В случае, если фильтрация происходит по закону Дарси,

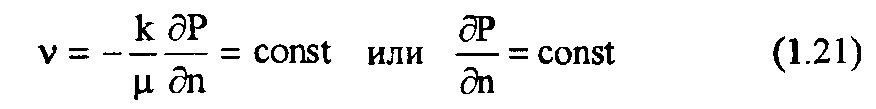
4. Модель открытого пласта с постоянным давлением на контуре питания, на внешней границе:

P(Rk,t)=Pk=const (1.22)

5. Переменный приток через границу (заданный, известный приток Rk):

Тема №3. Основная задача линейной теории упругого режима

В пласте образуется неустановившийся плоскорадиальный поток упругой жидкости. Предположим, что фильтрация однофазного флюида происходит по линейному закону Дарси при упругом режиме (при давлениях выше давления насыщения или начала конденсации). Распределение давления в любой точке пласта в любой момент времени P(r,t) определяется интегрированием уравнения пьезопроводности при следующих начальных и граничных условиях:

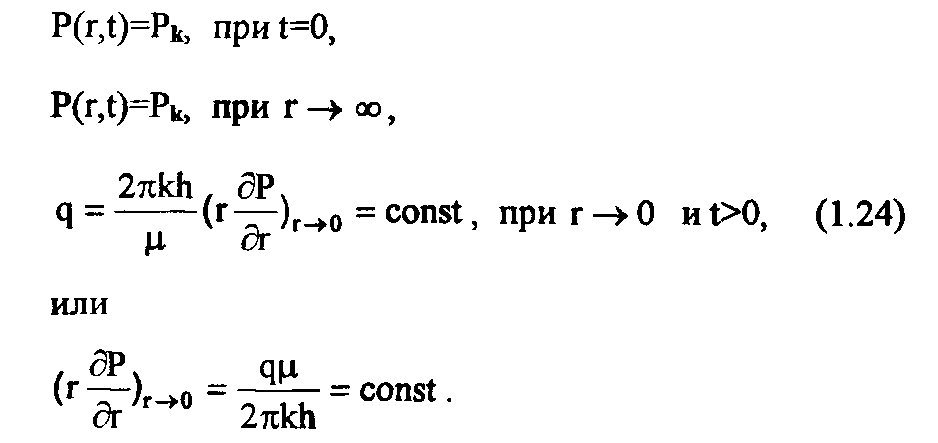
Решение уравнения пьезопроводности при данных условиях имеет вид:

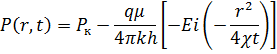
Где

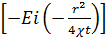– интегральная показательная функция.

Данная формула называется основной формулой теории упругого режима фильтрации, так как широко применяется на практике при интерпретации данных ГДИС, расчетах распределения давления в пласте в процессе разработки при фильтрации упругой жидкости и газа.

При малых значениях аргумента при интегрально показательной функции, данная функция аппроксимируется функцией:

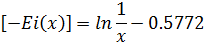
Т.е. давление в бесконечном пласте можно определять по приближенной простой формуле:

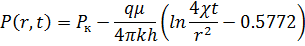
В частном случае при 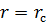(давление на забое скважины) изменение давления определяется формулой:

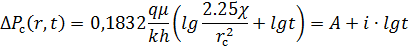
Тема №4. Метод касательной

Данные формулы являются основными расчетными формулами, применяемыми при обработке, анализе и интерпретации данных ГДИС на неустановившихся режимах при упругом режиме фильтрации. Так, из формулы следует, что графическое изображение зависимости изменения давления в скважине (КВД-КПД) от логарифма времени (т.н. полулогарифмическая анаморфоза) представляется с некоторого момента прямолинейным, где по уклону 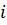и отрезку 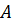, отсекаемому на оси ординат продолжением прямолинейного участка графика, возможно определение параметров пласта.

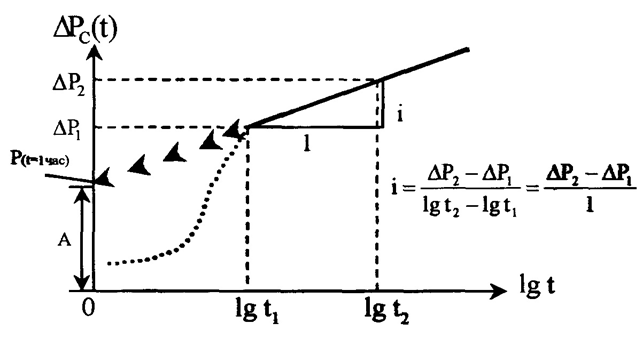
Рисунок 1 – Схематическое представление КПД-КВД в полулогарифмических координатах.

Простейший способ оценки параметров пласта по фактическим данным замеренных КПД-КВД схематически заключается в следующем:

1) фактическая КПД-КВД строится в полулогарифмических координатах;

2) по нанесенным точкам находится (выделяется) прямолинейный участок графика (в простейшем случае «на глаз» проводится прямолинейная касательная для точек в поздние моменты времени - по последним точкам; по методу наименьших квадратов с последовательным отбрасыванием начальных точек и определением коэффициентов корреляции или с помощью более сложных процедур линейного и нелинейного регрессионного анализа и др.). Этот пункт вызывает неопределенность в итоговых результатах;

3) затем по прямолинейному участку графика определяются численные значения его уклона i и отрезка А;

4) полагая, что фактическая КПД-КВД соответствует МПФС, описываемой уравнением (1.28), принимают

5) из этих соотношений по найденным i и А находят (оценивают) гидропроводность -

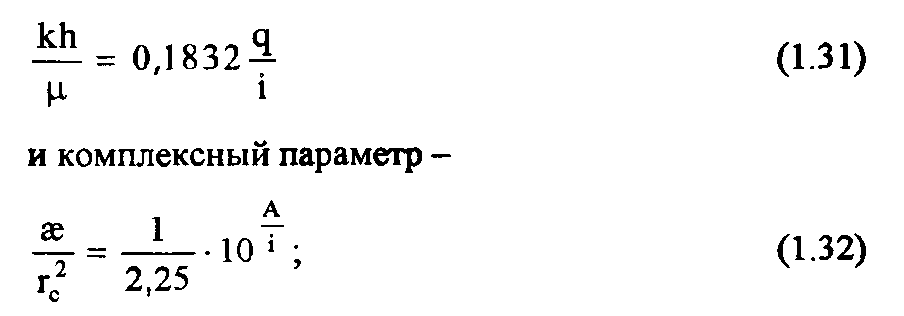
6) иногда предлагается последующее расчленение этих комплексных параметров, принимая известные значения вязкости 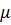,толщины пласта h, пористости m, упругоемкости 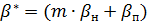и коэффициентов гидродинамического несовершенства скважин с целью оценки коэффициентов продуктивности (приемистости) скважины и пьезопроводности .

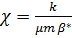Вышеизложенный простейший метод был предложен одним из первых и является традиционным и общепринятым. Часто его называют или методом обработки КПД-КВД без учета притока, или методом касательной, полулогарифмической анаморфозы, или методом МДХ (Миллера-Дайса-Хэтчинсона).

Основная трудность, сложность и неопределенность этого метода в изложенном варианте обработки заключается в необходимости предварительной оценки времени t₁ , начиная с которого нужно проводить прямолинейный участок КВД. Это время ti на замеренных КВД зависит от ряда факторов, вызванных несоблюдением внутренних граничных условий о мгновенном закрытии скважины (влияние ствола скважины и др.), которые могут искажать начальный участок реальных КВД и не учитывающихся в уравнении (1.28). Так, например, общее время t снятия КВД может быть очень коротким и меньшим t₁>t. Такую «короткую», фактическую КВД нельзя обрабатывать вышеизложенным методом (хотя прямолинейный участок может быть формально выделен согласно пункту 2), так как при этом могут быть получены ошибочные параметры пласта.

В работах отечественных и зарубежных исследователей метод без учета притока получил дальнейшее развитие с целью устранения этой неопределенности и более обоснованного выбора времени для начала прямолинейного участка КВД в полулогарифмических координатах.

Тема №5. Метод Хорнера

Пусть в некоторый момент времени в невозмущенном бесконечном однородном пласте с пластовым давлением Р_пл мгновенно пущена в работу добывающая скважина с постоянным дебитом q и через промежуток времени Т она мгновенно (т.е. на забое) остановлена - предполагается мгновенное прекращение притока жидкости к забою скважины. В интервале времени 0<t<T на забое происходит понижение забойного давления AP_c(t), которое описывается основной формулой теории упругого режима для РФП (1.28):

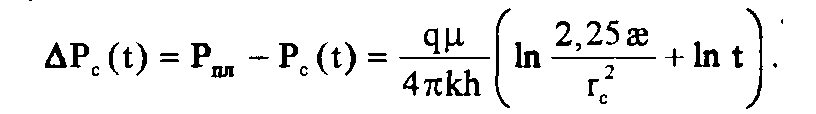
Для случаев фильтрации упругой жидкости в ограниченных открытых и закрытых пластах решения дифференциального уравнения (1) представляются более сложными формулами (бесконечными рядами по функциям Бесселя), чем для бесконечного пласта.

Начиная с момента остановки Т, которое принимается за начало отсчета времени снятия КВД происходит повышение забойного давления - Pc(t). Схематическое представление.

процесса изменения давления и дебитов при пуске и остановке скважины приведено на рисунке 2.

Рисунок 2 – Схема процессов изменения давления по методу суперпозиции

Для определения забойного давления в скважине в любой момент времени после ее остановки используется принцип суперпозиции. Так, следуя методу суперпозиции, мысленно допустим и заменим реальную картину изменения давления и дебитов другой - воображаемой эквивалентной картиной после остановки скважины. А именно, рекомендуется считать, что добывающая скважина не закрывается в момент времени Т, а продолжает работать и вызывает понижение давления в пласте и на забое скважины ∆P_c'(t) в моменты времени t>T:

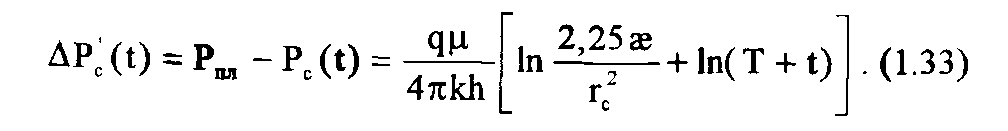
С момента времени Т в точке пласта, где расположена добывающая скважина, считается пущенной в работу воображаемая нагнетательная скважина (источник) с дебитом (приемистостью) «-q», которая вызывает повышение давления ∆P_c''(t):

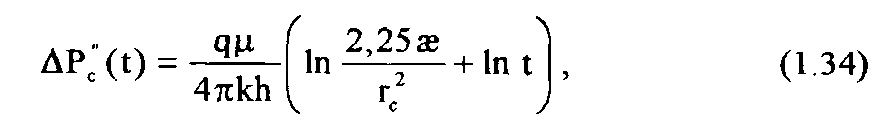
где t - время, отсчитываемое с момента остановки скважины.

Считается, что обе воображаемые скважины, добывающая и нагнетательная, при t>T работают независимо одна от другой. Таким образом выполняется условие задачи о закрытии скважины:

• дебит скважины после закрытия равен нулю: q=q+(-q)=0

• количество воображаемой нагнетаемой жидкости равно извлекаемому (рис. 1.11)

Тогда понижение давления, отсчитываемое с начального Рпл в момент времени t>T, определяется по методу суперпозиции наложением действий источника и стока:

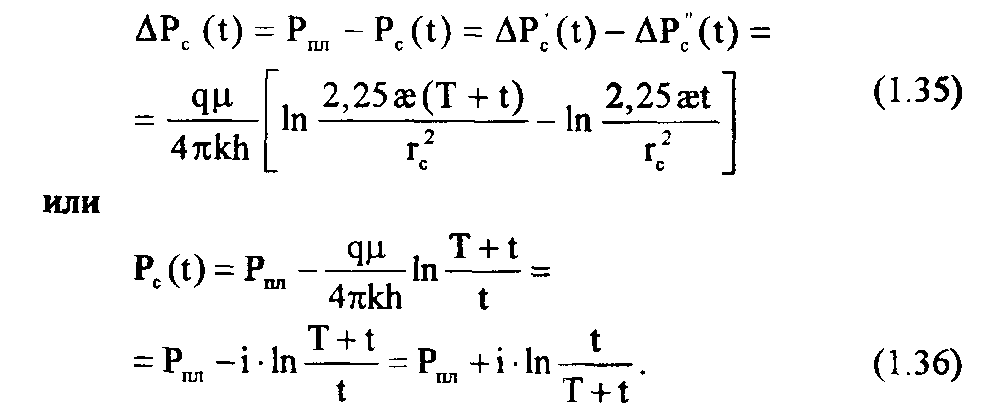
Формулу (1.36), характеризующую поведение КВД при выше сформулированных условиях, часто называют формулой Хорнера.

Метод Хорнера определения параметров пласта по КВД сводится к следующему. Фактическая КВД строится в координатах 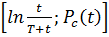, которые порой называют координатами Хорнера. Пользуясь диагностическими признаками, выделяют и проводят прямолинейный участок графика и находят уклон – 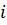, по величине которого определяется гидропроводность пласта, как и в методе касательной.

Тема №6. Влияния границ пласта на КВД

Реальные продуктивные пласты неоднородны и характеризуются различными геометрическими формами границ пласта, наличием прерывистости (непроницаемых и проницаемых барьеров, сбросов, сдвигов), зон с различными коллекторскими свойствами и изменением физических свойств насыщающих пласт флюидов,

Поэтому в теории ГДИС изучение влияния этих факторов на КВД и кривые гидропрослушивания (по данным исследования взаимодействия возмущающих и реагирующих скважин) представляет определенный практический интерес [4, 7, 13, 26 и др.]. Для изучения подобных задач в неоднородных пластах, в частности, используется метод суперпозиции. Для выполнения тех или иных условий на границах пласта и зон неоднородностей при этом приходится вводить фиктивные скважины-источники и скважины-стоки за пределами пласта.

Совокупность реальных и фиктивных скважин позволяет выполнять условия на границах пласта. Таким образом, изучение сводится к рассмотрению одновременной работы фиктивных и реальных скважин. Этот метод получил название метода зеркального отображения источников - стоков.

Целью подобного изучения, наряду с другими методами решения прямых и обратных задач подземной гидромеханики применительно к ГДИС, является получение основных расчетных формул МПФС и выделение соответствующих диагностических признаков для различных МПФС.

В качестве иллюстрации этой методологии рассмотрим некоторые простейшие случаи влияния формы границ пласта на КВД.

Рассмотрим особенности КВД в добывающей скв. 1, расположенной на расстоянии l вблизи прямолинейной непроницаемой границы (экрана) Г полубесконечного пласта (рис. 1.16) и пущенной в работу с дебитом q в момент времени t=0.

Применяя метод отображения источников - стоков зеркально отображают добывающую скв. 1 относительно непроницаемой границы Г воображаемой скв. 2 с дебитом «+q». В случае если вместо непроницаемого экрана находился бы прямолинейный контур питания с Р_k = const., то дебит скв. 2 был бы «-q». Таким образом, условия работы скв. 1 в полубесконечном пласте будут эквивалентны совместной работе скважин 1 и 2 в бесконечном пласте.

Динамику понижения давления в любой точке пласта М (которая может рассматриваться как реагирующая скважина) с непроницаемым экраном находят, используя принцип суперпозиции как сумму понижений давления, вызванных совместной работой скважин 1 и 2 в воображаемом бесконечном пласте [ 5, 7, 70, 71 и др.]:

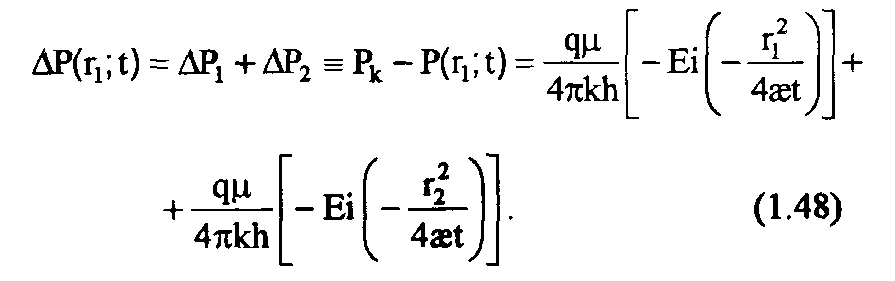
Забойное давление в скв. 1 находят, полагая r_i = r_c и заменяя функцию Ei(-x) ее аппроксимацией для малого аргумента в (1.48):

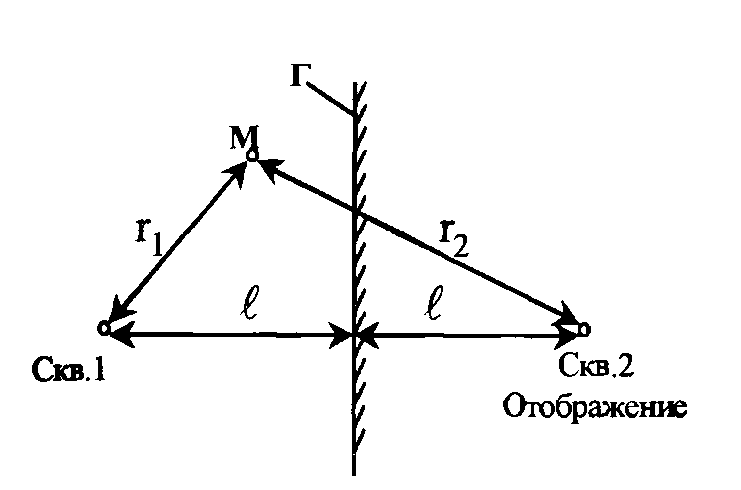
Рис. 1.16. Схема пласта с прямолинейной непроницаемой границей вблизи скважины Условные обозначения см. в тексте

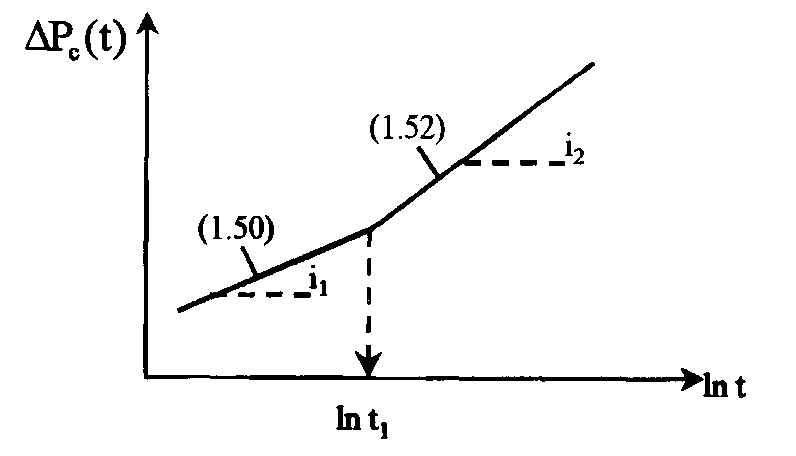
Рис. 1.17. Полулогарифмический график КВД-КГЩ в пласте с непроницаемой границей

• Уклон прямолинейного графика для ранних моментов времени i₁ в 2 раза меньше, чем уклон прямолинейного графика для поздних моментов времени i₂, т.е. график КВД-КПД состоит из двух прямолинейных участков с точкой пересечения в момент времени t1 (рис. 1.17). Причем, если имеется непроницаемый экран, то график КПД-КВД на втором участке отклоняется вверх, а если имеется контур питания, то отклоняется вниз:

• Наличие непроницаемого экрана проявляется в занижении в 2 раза гидропроводности по второму участку преобразованных КВД.

• В точке пересечения прямолинейных участков при t = t1 перепады давлений, подсчитанные по формулам (1.50) и (1.52), должны быть равны. Поэтому, приравнивая эти два выражения, можно найти расстояние до экрана:

Таким образом, для этой МПФС ДП является наличие двух прямолинейных пересекающихся участков, преобразованных КПД-КВД в полулогарифмических координатах. По найденным величинам уклонов, как и ранее, опре­деляются параметры пласта. Однако необходимо отметить, что при выделении двух прямолинейных участков могут возникнуть сложности:

• время ti может быть очень малым, начальный участок очень коротким, при очень небольшом расстоянии до сброса;

• начальный, прямолинейный участок может искажаться, маскироваться влиянием ствола Наконец, удвоение уклона второго прямолинейного участка полулогарифмического графика (диагностический признак) не гарантирует четкого и однозначного распознавания МПФС с непроницаемой границей вблизи скважины, так как подобные графики могут быть получены и при других видах ГДИС (КПД и КВД в нагнетательных скважинах, двух- и многоцикловых, снятии серии КВД-КПД при фильтрации аномально-вязких нефтей и др.).

Таким образом, нужно уметь отделять, разделять, распознавать влияние этих факторов для правильной интерпретации данных и выбора соответствующей МПФС.

В частности, задача определения МПФС с непроницаемой границей становится более определенной, если наряду с возмущающей скважиной одновременно исследуются две и более реагирующие скважины.