Прохождение микрочастицы через потенциальный барьер
(туннельный эффект)
Уникальным свойством квантовых частиц, в том числе и электронов, является их способность проникать через преграду даже в тех случаях, когда их энергия ниже потенциального барьера, соответствующего данной преграде. Это явление, т.е явление проникновения электрона через потенциальный барьер, в условиях, когда энергия электрона меньше высоты потенциального барьера, называется туннелированием (Т) (рыба проходит через стекло аквариума)..
Схематически оно представлено на рис.
Будь электрон классической частицей, обладающей энергией Е, он, встретив на своем пути преграду, требующую для преодоления большей энергии U, должен был бы отразиться от этой преграды. Однако как волна, он хотя и с потерей энергии, но проходит через эту преграду. Соответствующая волновая функция, а через нее и вероятность туннелирования рассчитываются из уравнений Шредингера. 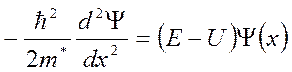
Эта вероятность тем выше, чем геометрически тоньше барьер и меньше разница между энергией падающего электрона и высотой барьера.
Туннелирование играет большую роль в МЭ, и особенно в НЭ. Этот эффект объясняет такие явления, как
· эмиссия электронов под действием сильного поля;
· прохождение тока через тонкие диэлектрические пленки;
· пробой р-п перехода.
В НЭ на эффекте туннелирования работают такие приборы, как резонансные туннельные диоды и транзисторы , одноэлектронные транзисторы, сканирующий туннельный микроскоп (СТМ).
Рассмотрим взаимодействие эектрона с потенциальным барьером. Задача 1-D (одномерная).
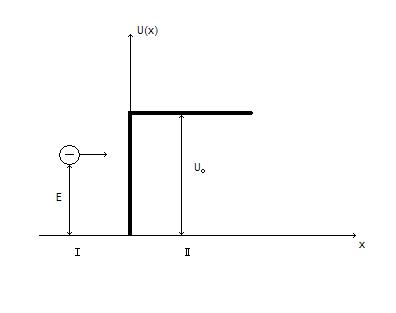
U0 при x > 0
U(x)=
0 при x < 0
Дя решения этой задачи пользуются я региональным методом нахождения волновых функций в отдельности для каждой из областей, а на их границе «склеивают» или «сшивают»полученное решение.
Условия склейки на границе потенциального барьера должны обеспечивать непрерывность волновой функции в точке х=0, а также непрерывность производных в этой точке.

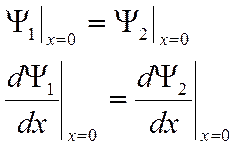
Для решения этой задачи необходимо найти волновую функцию, решая уравнение Шредингера:
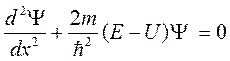
Для I области Для II области
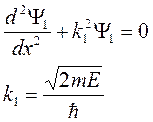
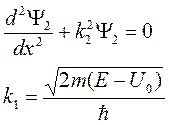
Общее решение для I области
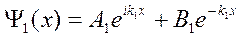
Для II области
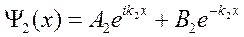
А1- амплитуда падающей волны;
В1 – амплитуда отраженной волны;
А2- амплитуда прошедшей волны;
В2 – амплитуда волны, двигающейся в противоположном направлении в области II.
Из физических соображений полагаем В2 равной 0 (т.к. х→∞ и волна отразиться не может), т.е. в области II нет условий для возникновения отраженной волны, тогда в области II
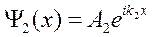
Дата добавления: 2016-04-14; просмотров: 1675;
