Что такое телесный угол?
Пусть L – некоторая замкнутая плоская линия, не имеющая самопересечений, S – некоторая точка, не принадлежащая плоскости, в которой лежит линия L (рис. 5.1).
Телесным углом W называется объединение всех лучей, имеющих общее начало в точке S и пересекающих часть плоскости, 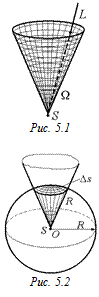 ограниченную линией L. Точка S называется вершиной телесного угла.
ограниченную линией L. Точка S называется вершиной телесного угла.
Телесный угол измеряется площадью поверхности, вырезаемой телесным углом на сфере радиуса R с центром в вершине телесного угла. Единица измерения телесного угла называется стерадиан (стер).
Один стерадиан – это такой телесный угол, который вырезает на поверхности сферы радиусом R фигуру площадью, равной R2 (рис. 5.2).
Чтобы измерить телесный угол, надо: 1) мысленно начертить сферу радиуса R с центром в вершине телесного угла; 2) найти площадь поверхности Ds, которую вырежет на сфере телесный угол; 3) вычислить телесный угол по формуле
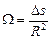 (стер).
(стер).
Пример 1. Полный телесный угол, охватывающий все пространство, равен
| Wполн = | Площадь поверхности сферы | = 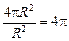 (стер). (стер).
|
| R2 |
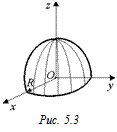 Пример 2. Частным случаем телесного угла является трехгранный угол, образованный в результате пересечения трех координатных плоскостей прямоугольной системы координат Охуz (рис. 5.3). Найдем этот угол.
Пример 2. Частным случаем телесного угла является трехгранный угол, образованный в результате пересечения трех координатных плоскостей прямоугольной системы координат Охуz (рис. 5.3). Найдем этот угол.
Пересечем этот телесный угол сферой радиуса R с центром в точке О. Поверхность сферы, вырезанная трехгранным углом, составляет 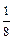 сферы. Тогда
сферы. Тогда
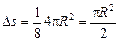 ;
;
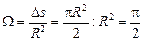 (стер).
(стер).
Пример 3.Конус с углом a при вершине и образующей R образует телесный угол W. Найдем этот угол.
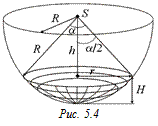 Пересечем конус сферой с центром в точке S и радиусом R. Тогда основание конуса будет прикрыто сферической «крышкой» – такая часть сферы называется сферическим сегментом.
Пересечем конус сферой с центром в точке S и радиусом R. Тогда основание конуса будет прикрыто сферической «крышкой» – такая часть сферы называется сферическим сегментом.
Площадь поверхности сферического сегмента Ds = 2prH, где
Н = R – h = R – Rcos(a/2)
– высота сегмента;
r = Rsin(a/2)
– радиус основания сегмента (рис. 5.4).
Отсюда
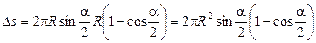 ;
;
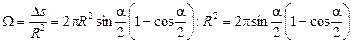 (стер).
(стер).
 Проверим правильность формулы:
Проверим правильность формулы:
1) пусть a = 0, тогда W = 0 (верно!);
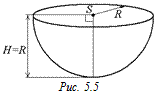
2) пусть a = p (рис. 5.5), тогда
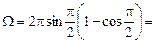
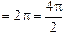 (стер) (верно!).
(стер) (верно!).
Заметим, что в задачах с симметрией удобно искать телесный угол как часть полного телесного угла, равного 4p (стер).
Пример 4. Найдем телесный угол, под которым видна из некоторой точки бесконечная плоскость. Ясно, что если плоскость бесконечна, то
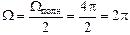 .
.
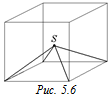 Пример 5. Найдем телесный угол, под которым видна из центра куба одна его грань (рис. 5.6). Ясно, что все шесть граней «видны» под полным углом, поэтому
Пример 5. Найдем телесный угол, под которым видна из центра куба одна его грань (рис. 5.6). Ясно, что все шесть граней «видны» под полным углом, поэтому
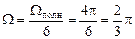 .
.
Дата добавления: 2016-04-11; просмотров: 10638;
