Принципы интегрирования рациональных функций
Важный класс функций, интегралы от которых всегда выражаются через элементарные функции, образуют так называемые рациональные функции, которые в самом общем случае можно представить в виде дроби:
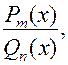
где 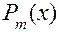 и
и 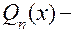 многочлены или целые рациональные функции степеней m и n, соответственно. Если степень многочлена в числителе больше или равна степени многочлена в знаменателе, т.е. m ³ n, то, выполнив деление, можно получить:
многочлены или целые рациональные функции степеней m и n, соответственно. Если степень многочлена в числителе больше или равна степени многочлена в знаменателе, т.е. m ³ n, то, выполнив деление, можно получить:
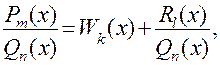
где 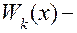 многочлен степени k, а степень многочлена
многочлен степени k, а степень многочлена 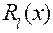 заведомо меньше степени многочлена
заведомо меньше степени многочлена 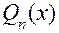 т.е. l < n.
т.е. l < n.
Таким образом, задача интегрирования «неправильной» дробно-рациональной функции всегда может быть сведена к задаче интегрирования многочлена, т.е. целой рациональной функции, а также к задаче интегрирования «правильной» дробно-рациональной функции.
Очевидно, что первая из них, т.е. задача интегрирования многочлена степени k, сводится к (k + 1) – кратному применению табличного интеграла 1. Для решения второй задачи необходимо предварительно разложить правильную дробно-рациональную функцию на сумму более простых, так называемых, элементарных дробей.
В курсе высшей алгебры доказывается, что любая правильная дробно-рациональная функция может быть единственным образом представлена в следующем виде:
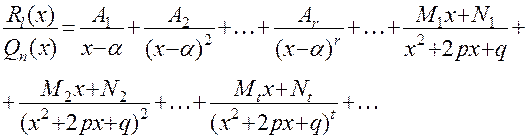 (*)
(*)
где α – любой действительный корень кратности r уравнения 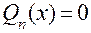 , (x2 + 2px + q) – неразложимый на линейные множители квадратный трехчлен, имеющий кратность t и также встречающийся при разложении на множители многочлена
, (x2 + 2px + q) – неразложимый на линейные множители квадратный трехчлен, имеющий кратность t и также встречающийся при разложении на множители многочлена 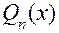 , наконец,
, наконец, 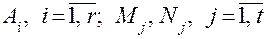 - некоторые, неизвестные числовые коэффициенты.
- некоторые, неизвестные числовые коэффициенты.
Чтобы определить значения этих коэффициентов, умножают обе части равенства (*) на 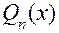 . Поскольку равенство между многочленом
. Поскольку равенство между многочленом 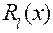 и многочленом, который получится в числителе правой части после приведения подобных, справедливо для всех x, кроме действительных корней многочлена
и многочленом, который получится в числителе правой части после приведения подобных, справедливо для всех x, кроме действительных корней многочлена 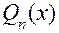 , то коэффициенты, стоящие при одинаковых степенях x в левом и правом многочленах, равны между собой. Таким образом, получают систему уравнений первой степени, в результате решения которой и находят искомые числовые коэффициенты. Изложенный метод носит название метода неопределенных коэффициентов.
, то коэффициенты, стоящие при одинаковых степенях x в левом и правом многочленах, равны между собой. Таким образом, получают систему уравнений первой степени, в результате решения которой и находят искомые числовые коэффициенты. Изложенный метод носит название метода неопределенных коэффициентов.
ПРИМЕР: Разложить функцию 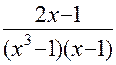 на элементарные дроби.
на элементарные дроби.
Поскольку: 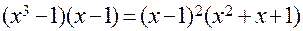 , заданную дробно-рациональную функцию можно представить в виде суммы элементарных дробей вида:
, заданную дробно-рациональную функцию можно представить в виде суммы элементарных дробей вида:
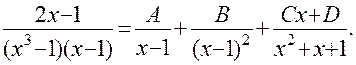
Умножая обе части последнего равенства на знаменатель исходной дроби, после приведения подобных получим:
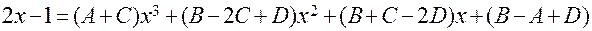
Приравнивая коэффициенты при одинаковых степенях x в правой и левой частях последнего равенства, получим систему уравнений вида:
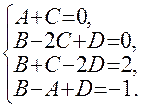
Решив ее, найдем: А = В = 1/3; С = - 1/3; D = - 1. Следовательно, искомое разложение имеет вид:
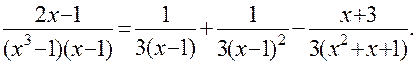
Как следует из рассмотрения формулы (*), после разложения правильной дробно-рациональной функции на сумму элементарных дробей задача ее интегрирования сводится к вычислению интегралов следующих четырех основных типов:
1). 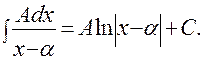 2).
2). 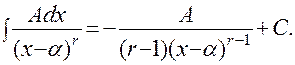
3). 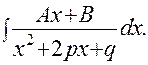 4).
4). 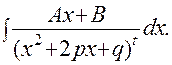
Первые два интеграла вычисляются сведением к табличным с помощью подстановки: t = x – α. В двух последних интегралах квадратный трехчлен, стоящий в знаменателе, действительных корней не имеет, т.к.: p2 – q < 0. Поскольку интегралы четвертого типа довольно редко встречаются на практике, а их вычисление связано с определенными трудностями, мы ограничимся только вычислением интеграла третьего типа.
Выделим из трехчлена, стоящего в знаменателе подынтегральной функции, полный квадрат: x2 + 2px + q = (x + p)2 + q – p2. Это выделение подсказывает подстановку: t = x + p; x = t – p; dx = dt.Обозначив q – p2 = h > 0, получим:
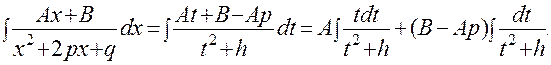
Первый из этих интегралов вычисляется непосредственно:
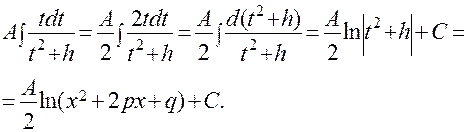
Второй – находится по формуле 13 таблицы интегралов:
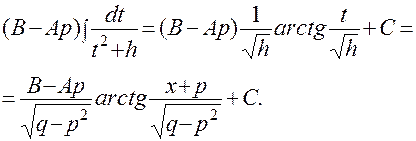
Поэтому окончательно можно записать:
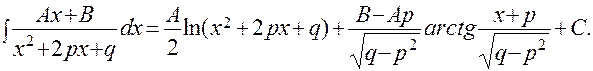
ПРИМЕР: Найти интеграл: 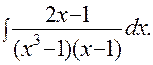
Используя результаты разложения подынтегральной функции на элементарные дроби, полученные в предыдущем примере этого подраздела, можно записать:
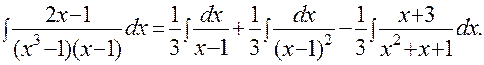
Для вычисления первых двух интегралов используем замену t = x – 1, x = t + 1, dx = dt и получим:
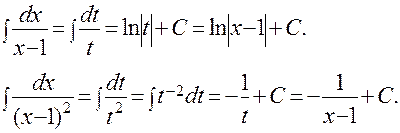
Для вычисления последнего, третьего интеграла воспользуемся полученной выше формулой, подставив в нее следующие числовые значения коэффициентов: А = 1, В = 3, p = 1/2 и q = 1, и получим:
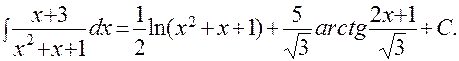
Учитывая числовые коэффициенты перед этими тремя интегралами, окончательно получим:
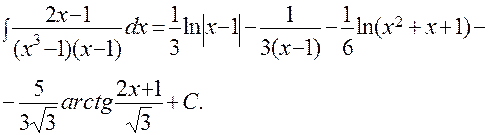
Дата добавления: 2016-04-11; просмотров: 925;
