Характеристики погрешности измерений
Рекомендация МИ 1317 – 2004 устанавливает следующие группы характеристик погрешности измерений:
1. Задаваемые в качестве требуемых или допускаемых – нормы характеристик погрешности измерений (нормы погрешности измерений).
2. Приписываемые любому результату измерений из совокупности результатов измерений, выполняемых по одной и той же аттестованной МВИ– приписанные погрешности измерений.
3. Отражающие близость отдельного, экспериментально полученного результата измерений к истинному значению измеряемой величины – статистические оценки характеристик погрешности измерений (статистические оценки погрешности измерений).
Нормы погрешности измерений, а также приписанные характеристики – представляют собой вероятные характеристики (характеристики генеральной совокупности) случайной величины – погрешности измерений. Эти нормы применяют преимущественно при массовых технических измерениях, выполняемых, например, при технологической подготовке производства, в процессе разработки, испытаний и эксплуатации продукции и т.п.
При измерениях, которые выполняются при проведении научно – исследовательских и метрологических работ (определение физических констант; свойств и состава стандартных образцов и т.п.) преимущественно применяют статистические оценки погрешности измерений. Они представляют собой статистические (выборочные) характеристики случайной величины – погрешности измерения.
В тоже время Рекомендация устанавливает следующие альтернативные вероятностные и статистические характеристики погрешности измерений:
1. среднее квадратическое отклонение погрешности измерений;
2. границы, в пределах которых погрешность измерений находится с заданной вероятностью;
3. характеристики случайной и систематической составляющих погрешности измерений.
Характеристики погрешности измерений и их статистическая оценка приведены в таблице 1.
Таблица 1.
| Характеристики погрешности измерений | Статистические оценки (по2.1.3) |
| Среднее квадратическое отклонение погрешности измерений | Оценка 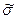 [Д] и (в случае необходимости) нижняя у1 [Д] и верхняя уh [Д] границы доверительного интервала, доверительная вероятность Pдов Д [Д] и (в случае необходимости) нижняя у1 [Д] и верхняя уh [Д] границы доверительного интервала, доверительная вероятность Pдов Д
|
| Границы, в которых погрешность измерений находится с заданной вероятностью | Оценка нижней 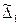 и верхней и верхней 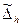 границ интервала, вероятность Р границ интервала, вероятность Р
|
| Характеристики случайной составляющей погрешности измерений: Среднее квадратическое отклонение нормализованная автокорреляционная функция Характеристики нормализованной автокорреляционной функции (например, интервал корреляции) | Оценка 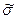 [ [ 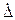 ] и (в случае необходимости) нижняя у1 [ ] и (в случае необходимости) нижняя у1 [ 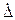 ] и верхняя уh [ ] и верхняя уh [ 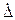 ] границы доверительного интервала, доверительная вероятность Pдов Д
Оценка функции ] границы доверительного интервала, доверительная вероятность Pдов Д
Оценка функции 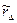 (ф)
Оценка характеристики (ф)
Оценка характеристики
|
| Характеристики неисключенной систематической составляющей погрешности измерений: среднее квадратическое отклонение неисключенной систематической составляющей границы, в которых неисключенная систематическая составляющая находится с заданной вероятностью | Оценка 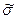 [Дs] и (в случае необходимости) нижняя у1 [Дs] и верхняя уh [Дs] границы доверительного интервала, доверительная вероятность Pдов s
Оценка нижней [Дs] и (в случае необходимости) нижняя у1 [Дs] и верхняя уh [Дs] границы доверительного интервала, доверительная вероятность Pдов s
Оценка нижней 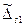 и верхней и верхней 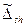 границ интервала, вероятность Рs границ интервала, вероятность Рs
|
В таблице 1 приведены обозначения для характеристик абсолютной погрешности измерений. Для обозначения характеристик относительной погрешности букву ∆ заменяют на д.
Рекомендуемое значение вероятности (доверительной вероятности) Р = 0,95 .
В особых случаях, например при измерениях, которые нельзя повторить, допускается указывать доверительные границы или расширенную неопределенность для уровня доверия Р и более высоких вероятностей.
Статистические оценки характеристик погрешности измерений представляют одной или при необходимости несколькими характеристиками и указывают их в единицах измерения (абсолютные) или процентах (долях) от результата измерения (относительные).
Дата добавления: 2016-04-06; просмотров: 2485;
