Законы Ома и Кирхгофа в символической форме
В символической форме можно представить не только отдельные синусоидальные функции времени, но и уравнения, содержащие такие функций. Рассмотрим последовательную цепь с R, L, С. Мгновенные значения напряжения и тока для такой цепи связаны, на основании второго закона Кирхгофа, уравнением:
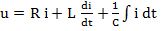 4.7
4.7
Пусть мгновенное значение тока в цепи определяется выражением
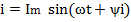
Тогда
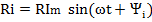
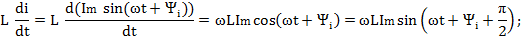
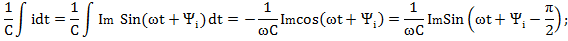
Полученным выражением соответствуют комплексные функции времени:
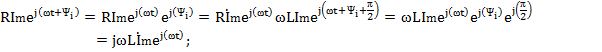
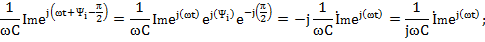
Здесь
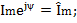
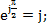
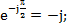
Напряжение на зажимах цепи является также синусоидальной функцией времени 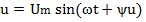 , которой соответствует комплексная функция
, которой соответствует комплексная функция
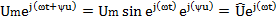
В соответствии с равенствам 4.5 мгновенные значения напряжений уравнения 4.7 представляют собой мнимые части соответствующих комплексных функций, взятые без множителя j:
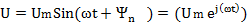
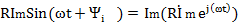
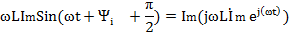
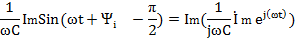
Поэтому
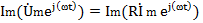 +
+ 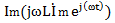 +
+ 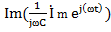
В данном случае при равенстве мнимых частей будут равны и действительные части комплексов напряжений, а следовательно равны и комплексные числа
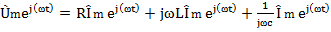 4.8
4.8
Разделим левую и правую части уравнения 4.8 на оператор вращения 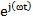 и на
и на 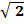 , получим:
, получим:
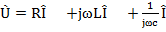 4.9
4.9
Сравнивая уравнения 4.7 и 4.9, можно сделать выводы:
а) для перехода от интегро-дифференциального уравнения к изображению в комплексной форме необходимо все мгновенные значения напряжений и токов заменить их комплексами; дифференцирование оригинала заменить умножением изображения на 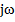 , а интегрирование оригинала—делением изображения на
, а интегрирование оригинала—делением изображения на 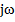
б) интетро-дифференциальному (или тригонометрическому) уравнению для мгновенных значений соответствует алгебраическое уравнение для изображений.
Таким образом, применение символического метода приводит к алгебраизации интегро-дифференциальных и тригонометрических уравнений, что позволяет применять для расчета цепей синусоидального тока все соотношения и законы цепей постоянного тока.
Из уравнения 4.9
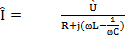 4.10
4.10
Полученное выражение представляет закон Ома в символической форме.
Величина, стоящая в знаменателе, называется комплексом полного сопротивления Z.
Комплекс полного сопротивления (или комплексное сопротивление) представляет собой комплексное число, действительная часть которого равна активному, а мнимая часть—реактивному сопротивлениям цепи.
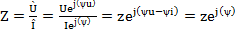 4.12
4.12
Модуль комплекса полного сопротивления равен полному сопротивлению цепи
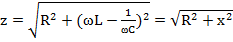 4.13
4.13
В выражении для комплекса полного сопротивления цепи
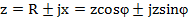
знак плюс перед мнимой частью ставится при индуктивном характере сопротивления (  > 0 ) и знак минус—при емкостном характере сопротивления (
> 0 ) и знак минус—при емкостном характере сопротивления (  <0).
<0).
При расчетах разветвленных цепей часто применяют комплексные проводимости, величины обратные комплексным сопротивлениям.
Комплекс полной проводимости равен:
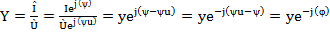 4.14
4.14
В тригонометрической и алгебраической формах комплекс полной проводимости имеет вид:
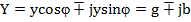 4.15
4.15
Модуль комплекса полной проводимости есть полная проводимость цепи, равная
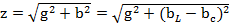 4.16
4.16
Действительная часть этого комплекса есть активная проводимость, а мнимая часть—реактивная проводимость.
Знак минус в выражении 4.15 перед мнимой частью ставится при индуктивном характере цепи (  >0), а знак плюс—при емкостном характере (
>0), а знак плюс—при емкостном характере (  <0).
<0).
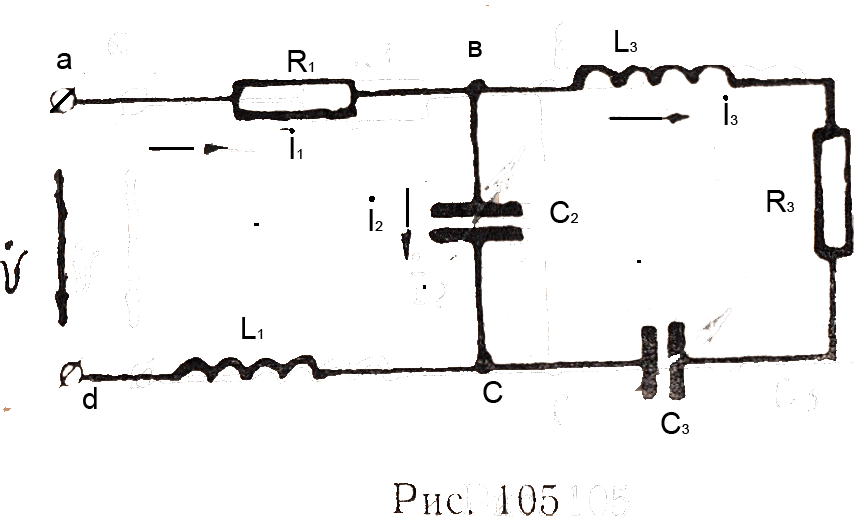
При изображении синусоидальных электрических величин в комплексной (символической) форме законы Кирхгофа имеют такой же вид, как и для цепей постоянного тока. Например, по первому закону Кирхгофа’ алгебраическая сумма комплексов токов, сходящихся в узле А (рис. 104), равна нулю, т.е. 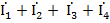 = 0 или в общем виде
= 0 или в общем виде
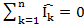 4.17
4.17
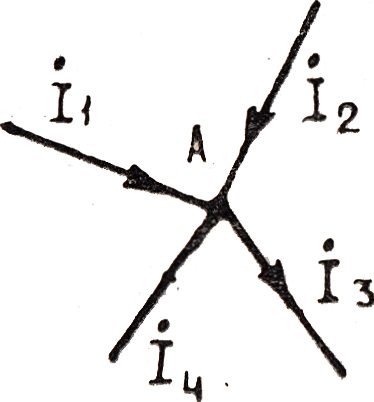
По второму закону Кирхгофа для замкнутого контура электрической цепи алгебраическая сумма комплексов э.д.с. действующих в контуре, равна алгебраической сумме комплексов падений, напряжений на отдельных участках этого контура. Так, для контура abed по второму закону Кирхгофа уравнение имеет вид:
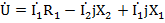
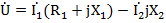 или
или 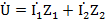 , где
, где 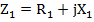
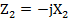
В общем виде уравнение по второму закону Кирхгофа записывается следующим образом:
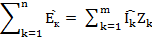 или
или 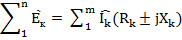
Пример 31. Определить ток в цепи если, активное сопротивление R = 80om,индуктивность L=90
мгн и конденсатор С = 35,5мкф, соединенные последовательно, включены в сеть с напряжением 220в и частотой 50гц.
Решение: Индуктивное сопротивление
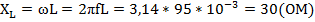
Емкостное сопротивление
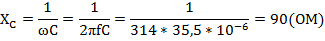
Комплекс полного сопротивления цепи
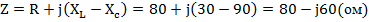
Комплекс тока в цепи по закону Ома
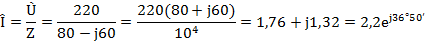
Действующее значение тока I =2,2 а. Так как начальная фаза напряжения, принята равной нулю( 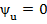 ) , то ток опережает напряжение на угол 36°50' (
) , то ток опережает напряжение на угол 36°50' ( 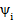 — 36°50') , т.е. угол сдвига фаз
— 36°50') , т.е. угол сдвига фаз
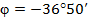 (характер цепи—емкостный).
(характер цепи—емкостный).
Пример 32. Катушка с активным сопротивлением R= 10 ом и индуктивностью L=95 мгн соединена параллельно с конденсатором емкостью С — 31,5 .мкф. Определить ток в цени 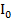 , если напряжение сети 220 в, частота 50 гц.
, если напряжение сети 220 в, частота 50 гц.
Решение. Индуктивное сопротивление
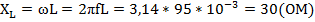
Емкостное сопротивление
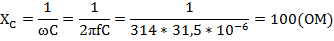
Комплекс полного сопротивления цепи
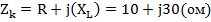
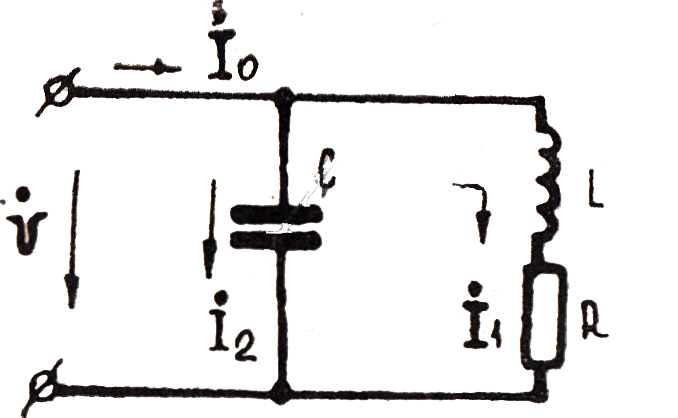
Рис. 106
Полная комплексная проводимость катушки
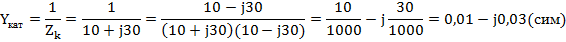
Комплексная проводимость конденсатора
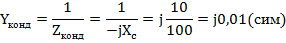
Полная комплексная проводимость всей цепи:
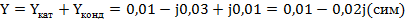
Ток в цепи (комплекс тока)
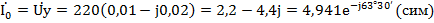
Характер сопротивления цепи активно-индуктивный, так как
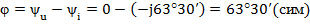
Дата добавления: 2016-04-06; просмотров: 3276;
