Определение теплового эффекта реакции нейтрализации
Опыт проводится в калориметре (риc. 3).
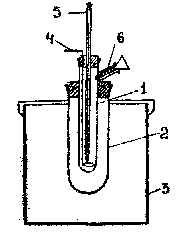
Рис.3. Стеклянный калориметр
Калориметр состоит из реакционного сосуда (1) емкостью 50 мл, помещенного в изотермическую оболочку (2) и (3). В пробке, закрывающей реакционный сосуд, имеются отверстия для мешалки (4) и термометра (5). Растворы реагирующих веществ наливают через боковой отросток (6).
Количество теплоты, выделяющейся или поглощающейся в калориметре, определяется по формуле: q = (tк - tн)ΣС, где tк - конечная температура; tн- начальная температура; ΣС - теплоемкость системы, состоящей из теплоемкости калориметрического сосуда и калориметрической жидкости: ΣС = С1m1 + С2m2, где С1 и m1 - удельная теплоемкость и масса реакционного сосуда; С2 и m2 - те же величины для жидкости, находящейся в калориметре (сумма массы воды и растворенного вещества). При использовании стеклянного реакционного сосуда его теплоемкостью можно пренебречь из-за его малой теплопроводности. Удельную теплоемкость растворов можно принять равной этой величине для воды, то есть С2 = 4,18 Дж /(моль·К). Стоит учесть, что тепловой эффект реакции нейтрализации сильных кислот сильными основаниями (щелочами) в разбавленных растворах не зависит от их природы, и взаимодействие определяется реакцией: Н+ + ОН- = Н2О (ж). Следовательно, при нейтрализации любой сильной кислоты сильным основанием должен наблюдаться практически одинаковый тепловой эффект ΔН0, что по мере разведения растворов реагентов приближается к предельной величине, равной: ΔН0298 = -55,9 кДж / моль (теплота нейтрализации).
Нейтрализации слабых кислот и оснований предшествует процесс диссоциации слабой кислоты (основания) на ионы, поэтому суммарная теплота нейтрализации в данном случае меньше, чем 55,9 кДж / моль, то есть, по закону Гесса можно определить теплоту диссоциации.
Данный опыт удобно выполнять вдвоем или втроем, так как необходимо одновременно перемешивать жидкость, следить по секундомеру, фиксировать положение ртутного столбика в термометре и производить запись экспериментальных данных.
Ход опыта:
Используя исходные 1н. растворы кислот и оснований, отмеряют в 4 стаканчика по 25 мл кислоты и основания в соответствии с полученной задачей (табл.1).
Т а б л и ц а 1
Индивидуальные задания по определению теплоты нейтрализации:
| Вариант | Задание | Вариант | Задание |
| NaOH + HCl NaOH + HАc | KOH + HCl NH4OH + HCl | ||
| NaOH + H2SO4 KOH + HАc | KOH + H2SO4 NH4OH + H2SO4 | ||
| NaOH + HNO3 NH4OH + HNO3 | NaOH + HNO3 KOH + HAc |
Через воронку внутреннего сосуда калориметра аккуратно переливают раствор кислоты во внутренний сосуд. В течение нескольких минут измеряют температурный ход калориметра при постоянном плавном перемешивании кислоты, фиксируют показания термометра с точностью до десятых долей градуса каждые 0,5 минуты. Если в ходе измерений в течение 5 минут изменение температуры равномерное или небольшое, начинают эксперимент, не прекращая перемешивать раствор кислоты.
Переливают через воронку во внутренний сосуд калориметра приготовленный раствор основания той же концентрации. Аккуратно перемешивают мешалкой раствор и следят за быстрым повышением температуры, пытаясь измерять температуру системы через возможно малые интервалы времени (5-10 с). Фиксируют максимальное значение (tк) ("скачок" температуры).
После того, как рост температуры прекратится и станет равномерно снижаться, продолжают измерения еще не менее 3 минут при постоянном перемешивании раствора.
По результатам опыта строят на миллиметровой бумаге график в координатах температура (t, 0C) - время (мин), аналогичный приведенному на рис. 4.
При построении графика следует помнить, что поскольку все измерения (времени и температуры) проводятся с определенной ошибкой, наблюдается некоторый разброс экспериментальных данных. Поэтому линии на графике проводят не строго через экспериментальные точки, а в виде плавной кривой. Уточняют по графику Δt реакции.
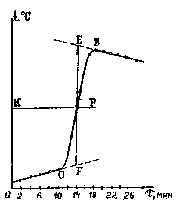
Рис. 4. График изменения температуры во времени
Определяют общую массу раствора: mр-ра = mк. + mщ. = Vкrк + Vщrщ, где Vк, Vщ - объемы (мл); rк , rщ - плотность (г / мл) кислоты и щелочи соответственно;
r Н2SO4 = 1,070; r HNO3 = 1,035; r NaOH = 1,0460;
r HCl = 1,023; r KOH = 1,050
Определяют количество выделившегося тепла: q = 4,18 ·mр-ра ·(tк - tн). Для определения теплового эффекта (энтальпии ΔНнейтр) реакции перечисляют количество выделившегося тепла на 1 эквивалентную массу.
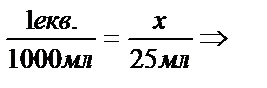 х =
х = 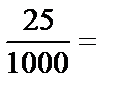 0,025 экв. Q =
0,025 экв. Q = 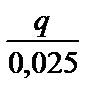 Дж; Q =
Дж; Q = 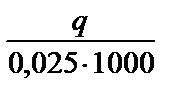 кДж Þ DНнейтр=-Q.
кДж Þ DНнейтр=-Q.
Оценивают погрешность полученного значения теплоты нейтрализации относительно табличного значения:
П = 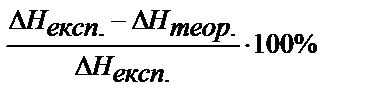
Зная, что при образовании 1 моль воды из ионов при комнатной температуре выделяется 55,9 кДж, по закону Гесса определяют теплоту диссоциации уксусной кислоты или гидроксида аммония:
DН0дисс. = -55,9 - DН0нейтр .
Результаты вычислений заносятся в таблицу.
В выводах укажите:
- На основании экспериментальных и расчетных данных оцените силу изученных кислот и оснований;
- Почему тепловой эффект этой реакции для сильных кислот и щелочей в разбавленных растворах не зависит от их природы?
- Объясните отклонения экспериментально полученной теплоты нейтрализации от теоретической.
Опыт 2. Определение теплоты гидратации соли (элементы НИРС)
Общие указания:
При выполнении данного опыта необходимо помнить, что теплотой гидратации является количество тепла, затрачиваемое на образование 1 моль твердого кристаллогидрата из твердой безводной соли и соответствующего количества воды. Эту величину находят расчетным путем, основываясь на калориметрических данных по теплотам растворения безводной соли и кристаллогидрата в достаточно больших количествах воды.
Процесс образования раствора безводной соли МеХn в воде осуществляется в две стадии: 1)процесс образования кристаллогидрата МеХn·mН2O; 2)растворение МеХn·mН2O:
1) МеХn (тв.) + mН2О ® МеХn×mН2 O(тв.) DН01 ;
2) МеХn×mН2O + aq ® МеХn(раствор) + mН2O DН02 .
Суммарный тепловой эффект DН01 + DН02 равен теплоте растворения безводной соли (согласно закону Гесса): МеХn + aq ® МеХn(раствор) , DН03 . Теплота гидратации (DН01) определяется по уравнению:
DН01 = DН03 - DН02 .
Ход работы:
1. Определение постоянной калориметра:
а) по известной теплоте растворения КNО3
Тепловой эффект процесса, протекающего в калориметре (ΔН), можно рассчитать, измерив точно скачок температуры Δt в результате опыта: ΔН0 = К·Δt, где К - постоянная калориметра. По физическому смыслу постоянная является теплоемкостью калориметра, численно равная количеству тепла, необходимого для нагревания всех частей калориметра на один градус. Постоянную калориметра определяют по известной теплоте растворения какой-либо соли, например, КNО3.
Для этого тщательно растирают соль в фарфоровой ступке и взвешивают с точностью до 0,01 г 2 г соли. Реакционный сосуд заполняют точно 50 мл дистиллированной воды, закрывают ее пробкой и закрепляют в ней термометр и мешалку. После установления постоянного значения температуры в калориметре, быстро высыпают навеску нитрата калия и, размешивая аккуратно раствор, наблюдают за изменением температуры, записывая показания термометра каждые полминуты. Рассчитывают Δt после того, как указано выше.
Определяют значение постоянной калориметра К по уравнению:
К = 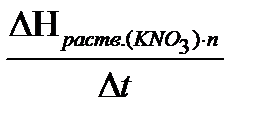 , где DН0раств.(КNО
, где DН0раств.(КNО  ) - известная теплота (энтальпия) растворения нитрата калия, равная 34,93 кДж / моль при 298 К; n - количество молей соли КNО3.
) - известная теплота (энтальпия) растворения нитрата калия, равная 34,93 кДж / моль при 298 К; n - количество молей соли КNО3.
б) по известному количеству теплоты q, сообщенного калориметру.
Калориметрической системе за промежуток времени D 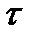 предоставляется известное количество теплоты q и измеряется соответствующее изменение температуры Δt . Количество тепловой энергии q, сообщенное калориметрической системе при электронагреве, определяется по формуле Джоуля: qэл. = (U2× D
предоставляется известное количество теплоты q и измеряется соответствующее изменение температуры Δt . Количество тепловой энергии q, сообщенное калориметрической системе при электронагреве, определяется по формуле Джоуля: qэл. = (U2× D 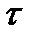 )/ r, где U - напряжение постоянного тока, подаваемая на нагреватель, В; r - сопротивление нагревателя, Ом; D
)/ r, где U - напряжение постоянного тока, подаваемая на нагреватель, В; r - сопротивление нагревателя, Ом; D 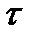 - время нагрева калориметра, с. Тогда постоянная калориметра:
- время нагрева калориметра, с. Тогда постоянная калориметра:
К = qэл./D t .
2. Определение теплоты растворения безводной соли и ее кристаллогидрата
Для проведения опыта используют навески солей, полученных у преподавателя в соответствии с вариантами заданий (табл. 2).
Т а б л и ц а 2
Варианты заданий и значение ΔНо растворения солей
| Вариант | Соль | DНраств , кДж/моль |
| СuSО4 СuSО4×5H2O | -66,5 11,70 | |
| CuCl2 CuCl2×2H2O | -46,5 -15,50 | |
| MgSO4 MgSO4×7H2O | -84,96 16,1 | |
| Na2SO4 Na2SO4×7H2O | -2,11 78,51 | |
| Na2CO3 Na2CO3×10H2O | -24,60 66,58 | |
| BaCl2 BaCl2×2H2O | -8,6 20,59 | |
| CoCl2 CoCl2×6H2O | -77,21 11,19 | |
| Co(NO3)2 Co(NO3)2×6H2O | -50,01 20,80 | |
| FeSO4 FeSO4×7H2O | -62,36 18,9 |
Соль берут в количестве 0,005-0,01 моль и взвешивают с точностью до 0,01 г, предварительно растерев в порошок. В калориметр наливают точно 50 мл дистиллированной воды, закрепляют термометр и мешалку. В течение нескольких минут измеряют температурный ход калориметра при постоянном плавном перемешивании воды, фиксируя показания термометра с точностью до десятых долей градуса каждые 0,5 минуты.
Если в ходе измерений в течение 5 минут изменение температуры равномерное или небольшое, начинают эксперимент, не прекращая перемешивать воду: быстро высыпают в калориметр навеску соли и, перемешивая раствор, проводят измерения температуры до полного растворения соли (примерно в течение 2-3 минут). Фиксируют максимальное значение (tк). После того, как рост температуры прекратится и температура станет равномерно снижаться, продолжают замеры еще 3-4 минуты при постоянном перемешивании раствора.
Обработка данных и вычисления:
По результатам опыта рисуют на миллиметровой бумаге график в координатах температура (t,0C) - время (τ, мин.), аналогичный приведенному на рисунке 4, по которому уточняют значение Δt. (Более точно Δt определяют с помощью метастатического термометра Бекмана, правила работы с которым необходимо выяснить у преподавателя).
Молярную интегральную теплоту растворения соли и ее кристаллогидрата DНраств МеХn×m Н2O определяют по формуле:
DН0раств. = (К×Dt)/n, где n = 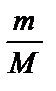 , m и М - навеска и молекулярная масса безводной соли или кристаллогидрата.
, m и М - навеска и молекулярная масса безводной соли или кристаллогидрата.
Определяют теплоту гидратообразования по формуле:
DН0гидр. = DН0раств. МеХn - DН0раств. МеХn×mН2О .
Рассчитывают теоретическое значение теплот гидратации солей, пользуясь справочными данными. Находят относительную ошибку определения. Полученные результаты заносят в таблицу 3 .
Таблица 3
Экспериментальные данные для расчёта значения DН0раств
| Соль | m, г | n, моль | Dt | Значения DН0раств | Относит. ошибка, % | |
| табл. | эксп. | |||||
| МеХn | ||||||
| МеХn×mН2 О |
В выводах укажите: как с помощью следствий из закона Гесса можно определить ΔН0 гидратации?
Скорость протекания химических реакций и химическое равновесие
Химическая термодинамикапредусматривает лишь возможность самопроизвольного протекания процесса. На вопрос о том, как быстро осуществится эта возможность, отвечает химическая кинетика - раздел химии, изучающий скорость и механизм химических превращений. Скорость любой химической реакции определяется изменением концентрации одного из реагирующих веществ в единицу времени. Очевидно, скорость реакции обусловлена числом элементарных актов реакции за единицу времени в единице объема (для гомогенных реакций) или на единицу поверхности раздела фаз (для гетерогенных реакций).
На скорость реакции влияют многочисленные факторы: природа реагирующих веществ, концентрация реагентов, температура, наличие катализатора или ингибитора, давление (для газов), степень измельчения (для гетерогенных систем), природа растворителя, форма реактора (для цепных реакций), интенсивность света (для фотохимических процессов), высокочастотное излучение и так далее. Таким образом, химическая кинетика - это большой раздел химии, задачей которого является определение всех кинетических факторов с целью целенаправленного воздействия на направление и скорость реакции для достижения максимального желаемого результата. По программе для инженерных специальностей в курсе общей химии студенты знакомятся только с основными положениями химической кинетики.
Необходимым условием протекания химического процесса является столкновение молекул. Поэтому необходимо внимательно рассмотреть положения теории активных столкновений, согласно которой число активных столкновений (Nа) равно:
Nа = N0 . e-Ea/RT , откуда: kT = P . Z. e-Ea/RT ,
где N0 - постоянная Максвелла-Больцмана; kT - константа скорости реакции при температуре Т; P - фактор вероятности (стерический фактор), который требует определенной ориентации в пространстве молекул при столкновении (фактор доступности реакционного центра); Z - частотный фактор, то есть число столкновений в единице объема за единицу времени при концентрации, равной единице; Еа - энергия активации, это избыток энергии, который должны иметь реагирующие молекулы по сравнению со средней энергией всей системы, чтобы между ними произошла реакция. Энергия активации - это тот минимум энергии ("энергетический барьер"), который необходимо преодолеть для перехода реагирующих молекул в состояние активного комплекса (теория активного комплекса).
A B A … B A — B
| + |  : :
: :  +
+
A B A … B A — B
исходное состояние переходное состояние конечное состояние
(исходные реагенты) (активированный комплекс) (продукты реакции)
Для термодинамически разрешенных (ΔG0<0) реакций найдено, что реакция происходит с достаточной скоростью при условии Еа< 150 кДж / моль. Например: NO + ½ O2 → NO2 (бесцветный газ NO в воздухе превращается очень быстро в бурый газ NO2). Энергия активации для этой реакции равна ≈ 80 кДж / моль.
Основной закон химической кинетики - закон действующих масс (К.М.Гульдберг, П. Вааге, 1867 г.), который для гомогенной реакции: аА + bВ → cC + dD имеет математическое выражение:
υ = k·[А]а·[В]b
Для гетерогенных реакций надо учитывать удельную поверхность (S): при значительной дисперсности (раздробленности) твердого вещества величина общей поверхности входит в кинетического уравнения. Например, если А - твердое вещество, то:
υ = k·SА·[В] b
Для газов в математическом выражении закона действующих масс концентрацию заменяют парциальным давлением газообразных веществ: υ = k . РАa . РВb . Константа скорости по физическому смыслу - это скорость реакции при условии, что концентрации (или давления - для газов) реагирующих веществ равны единице. Тогда: υ = k.
Зависимость скорости реакции от температуры выражает эмпирическое правило Я.Вант-Гоффа (1884 г.) При повышение температуры на каждые 10 градусов скорость реакции увеличивается в 2 - 4 раза: υt2 /υt1 = γΔt/10, где γ - температурный коэффициент Я.Вант-Гоффа).
Более универсальной характеристикой зависимости скорости реакции от температуры является уравнение С.Аррениуса:
kT = A.e-Ea/RT , или: lnk = lnA - Ea/RT .
Логарифмически это выражение представляет собой уравнение прямой в координатах lnk - 1 / T, тангенс угла наклона которой (tg α) равен Еа / R. То есть, энергию активации реакции можно определить по данным эксперимента.
Следует обратить внимание на механизм действия катализаторов и использование их для ускорения химических процессов. Во всех случаях суть катализа - снижение энергии активации в реагирующей системе. В некоторых случаях на практике применяют ингибиторы ("антикатализаторы") - вещества, замедляющие химический процесс.
Вопрос химического равновесия следует рассматривать, исходя из того, что все химические реакции можно разделить на обратимые и практически необратимые. В момент наступления равновесия прямая и обратная реакции не прекращаются, а продолжают протекать с равными скоростями, то есть равновесие является динамичным. Для реакции, записываемой в общем виде: aА+bВ ↔ cС+dD в состоянии равновесия, выполняется соотношение: 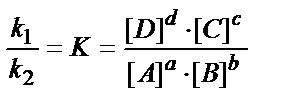 ,
,
где k1, k2 - константа скорости прямой и обратной реакции; К - константа равновесия.
Следует отметить, что в выражении константы равновесия гетерогенных реакций входят только концентрации веществ, находящихся в жидкой и в газовой фазе, так как концентрации твердых веществ условились считать постоянными (равными 1). Значение константы равновесия не зависит от концентрации, парциальных давлений для реакций в газовой фазе, но зависит от природы реагирующих веществ и температуры. Использование катализаторов не изменяет константу равновесия, а лишь сокращает время, необходимое для достижения состояния равновесия.
Состояние химического равновесия сохраняется до тех пор, пока внешние условия остаются неизменными. При изменении внешних условий (концентрация, давление, температура) система выходит из состояния равновесия, так как скорость прямой и обратной реакции изменяются в неодинаковой степени. Влияние, оказываемое на равновесную систему внешним воздействием, можно предположить, пользуясь принципом Ле-Шателье: если на систему, находящуюся в равновесии, подействовать извне, то равновесие сместится в таком направлении, при котором это влияние будет ослаблено или устранено. Так, при введении в систему одного из реагентов равновесие смещается в сторону его расходования, при повышение давления - в сторону меньшего объема газов, при повышение температуры - в сторону эндотермической реакции.
Задача 1. Как изменится скорость прямой реакции 2NO + Br2 → 2NOBr, если давление в системе увеличить в 3 раза?
Решение. Обозначим исходные давления NO через Р1, а Br2 через Р2, тогда скорость реакции равна: υ1 = kp×P21×P2. При увеличении общего давления в три раза парциальные давления тоже увеличатся в три раза NO = 3P1, Br2 = 3P2, а скорость реакции υ2 = kp×(3P1)2×(3P2). Þ υ2/υ1= 27. Таким образом, скорость возрастает в 27 раз.
Задача 2. Как возрастет скорость реакции при повышении температуры от 10 до 1000С, если температурный коэффициент скорости равен 2?
Решение. Используем правило Вант-Гоффа
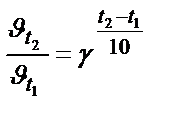 ;
; 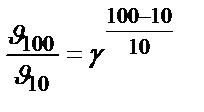 = 29 = 512.
= 29 = 512.
. Скорость возрастет в 512 раз.
Задача 3. Для равновесной системы СО + Н2О ↔ СО2 + Н2 константа равна: К = 1. Определить концентрации всех веществ в состоянии равновесия, если начальные концентрации [CO] = 2 и [H2O] = 3 моль / л.
Решение. Для данной равновесной системы выражение константы равновесия имеет вид: К= 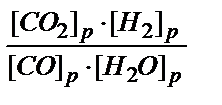
Обозначим [СО2]равн = [Н2]равн = [СО]расх. = [Н2О]расх. = х, где [СО2]равн, [Н2]равн - соответствующие равновесные концентрации, а [СО]расх, [Н2О]расх - израсходованные концентрации.
Поскольку СОравн = СОнач.– СОрасх., то [СО]равн = (2-х), [Н2О]равн = (3-х). То есть, 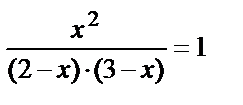 , откуда х = 1,2 моль / л.
, откуда х = 1,2 моль / л.
Итак, [СО]равн = 2 - 1,2 = 0,8 (моль / л); [Н2О]равн = 3 - 1,2 = 1,8 (моль / л), [СО2]равн = [Н2]равн = 1,2 (моль / л).
Дата добавления: 2016-02-27; просмотров: 9356;
