Основные расчетные выражения и необходимые пояснения. Диэлектрическая проницаемость

Диэлектрическая проницаемость. Диэлектрики

Основные расчетные выражения и необходимые пояснения

Диэлектрическая проницаемостькак параметр материала характеризует поведение в электрическом поле зарядов вещества связанных в атомы, молекулы, кристаллы (не свободных). При воздействии на материал внешнего электрического поля с напряжённостью Е_{пустоты}, имеющего плотность потока электрического смещения D_внешн=ε₀Е_{пустоты}, в нем происходит поляризация (смещение (r) связанных зарядов, (q) в соответствии с их знаком и направлением поля). Поляризацию обозначают вектором поляризации Р. Вектор поляризации Р равен сумме дипольных моментов (q×r) в единице объёма материала (V) и направлен против внешнего поля:

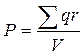(1.1)

В результате поляризации напряжённость поля в материале уменьшается с Е_{пустоты} до Е_{материала}. Поэтому поток электрического смещения воздействующего на материал поля можно приравнять сумме двух векторов:

D_внешн = ε₀ Е_{материала} + Р (1.2)

Отсюда получаем:

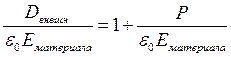
(1.3)

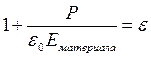Относительная величина

(1.4)

называется диэлектрической проницаемостью материала и обозначается ε.

Обычная форма записи, связывающая внешний поток электрического смещения D_внешн с напряжённостью поля в материале Е_{материала} , вытекает из (1.3) и (1.4) и выглядит как:

D_внешн = ε₀ ε Е_{материала}. (1.5)

В пустоте нет частиц, которые могли бы поляризоваться (q=0), поэтому Р=0, а диэлектрическая проницаемость ε=1. Для пустоты:

D_внешн = ε₀ Е_{пустоты}. (1.6)

Из (1.5) и (1.6):

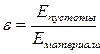. (1.7)

Таким образом, можно дать следующие определения диэлектрической проницаемости:

1). Диэлектрическая проницаемость, ε является мерой поляризации вещества в электрическом поле (см. 1.4).

2) Диэлектрическая проницаемость, ε - это мера ослабления поля в веществе по сравнению с внешним полем; её значение показывает во сколько раз поле в веществе слабее поля от того же источника в вакууме (см. 1.7).

3) Диэлектрическая проницаемость, ε является также мерой ёмкости, которую может создать диэлектрик. Значение диэлектрической проницаемости вещества, εможно определить как отношение ёмкости конденсатора с данным веществом (диэлектриком) к ёмкости конденсатора тех же размеров, диэлектриком которого является вакуум (см. ниже).

Для получения количественных результатов при выполнении задания необходимо вспомнить, что заряд какого либо устройства - q есть произведение ёмкости этого устройства C на приложенное к устройству напряжение U:

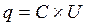(1.8)

Если ёмкость определяется по отношению к земле, потенциал которой принимается равным нулю, вместо напряжения U используется значение “потенциала” (j) того тела, ёмкость которого определяется.

Для расчета ёмкости необходимо четко представить конфигурацию поля в рассчитываемом устройстве.

В заданиях по теме 1 используются электрические поля следующих конфигураций:

- плоско- параллельное,

- радиально-цилиндрическое,

- радиально-сферическое.

Ниже приводится описание этих полей и необходимые для расчета формулы.

Плоскопараллельное поле.

В плоско-параллельном поле эквипотенциальные поверхности (поверхности равного потенциала, поверхности уровня) представляют собой параллельные плоскости, а линии потока смещения D, совпадающие с направлением вектора напряженности поля E, - параллельны друг другу и перпендикулярны этим плоскостям.

Значение ёмкости:

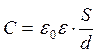, (1.9)

В плоскопараллельном

поле напряжённость Е

одинакова во всех точках.

Поэтому:

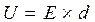(1.10)

По выражениям (1.9) и (1.10) рассчитываются параметры плоских конденсаторов.

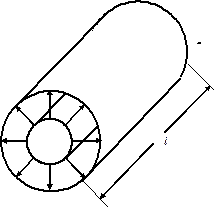
Радиально-цилиндрическое поле.

Эквипотенциальными в этом поле являются коаксиальные (имеющие общую ось) цилиндрические поверхности, а линии смещения располагаются по радиальным направлениям.

Значение ёмкости

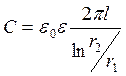, (1.11)

r₁- радиус внутреннего цилиндра;

r₂- радиус внешнего цилиндра.

По выражению (1.11) можно рассчитать ёмкость одножильного коаксиального кабеля (например, кабеля для телевизионной антенны или одножильных кабелей на напряжение 110…500 кВ).

Радиально-сферическое поле.

В этом поле поверхности уровня - это сферы с общим центром, а линии смещения направлены по радиусам.

Значение ёмкости:

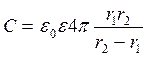, (1.12)

причем, ёмкость шара по отношению

к сфере бесконечного радиуса ( ):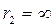

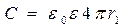, (1.13)

Ёмкость полушария в два раза меньше.

Кроме приведённых выражений полезно будет также вспомнить соотношение для плотности потока смещения D, когда силовые линии от заряда q походят перпендикулярно в каждой тоске поверхности S:

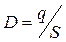(1.14)

Если поток смещения одинаковой плотности пронизывает диэлектрики с различной диэлектрической проницаемостью, то справедливо соотношение (вытекающее из 1.5):

ε₁ Е₁=ε₂ Е₂ (1.15)

Отсюда следует, что значения напряжённости поля обратно пропорциональны диэлектрическим проницаемостям:

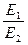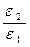= (1.16)