Логарифмические частотные характеристики
Пусть задана частотная передаточная функция
W(jω)=A(ω)⋅e jφ(ω)
Прологарифмируем :
lnW(jω)=lnA(ω)+jφ(ω) ,
то есть логарифм W(jω) – это комплексное выражение, где действительная часть– ln модуля, а мнимая часть – фаза.
Для практических целей удобно пользоваться десятичными логарифмами и строить отдельно логарифмическую амплитудную частотную характеристику (ЛАЧХ) и логарифмическую фазовую частотную характеристику (ЛФЧХ). Для построения ЛАЧХ находится величина
L(ω)= 20lgW(jω)= 20lg A(ω).
L(ω) – измеряется в децибелах [дБ]. Бел – это такое усиление, когда мощность увеличивается в 10 раз (1Б=10дБ), 2 Бела – усиление в 100 раз. Крупные единицы: декабелы, гектобелы и т. д. Мелкие единицы: децибелы, сантибелы и т. д.
По оси абсцисс откладывается частота ω в логарифмическом масштабе, то есть наносятся отметки, соответствующие lgω, а около них пишется само значение частоты ω, [рад/с].
Единицами измерения lgω являются октава и декада.
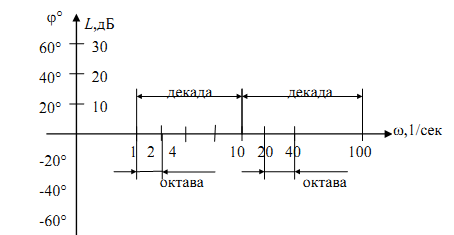
Декада– это интервал частот, заключенный между произвольным значением ω и 10ω. lg10ω −lgω =lg10=1, то есть отрезок между ω и 10ω не зависит от абсолютного значения ω.
Октава– интервал частот, заключенный между произвольным значением ω и 2ω.
lg2ω−lgω=lg2, тоже не зависит от абсолютного значения ω. Практически для нанесения логарифмического масштаба можно пользоваться выражением:
Логарифмические характеристики обладают двумя ценными свойствами:
1. ЛАЧХ и ЛФЧХ для произведения вычисляются как суммы ЛАЧХ и ЛФЧХ отдельных звеньев:
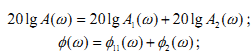
2. В области высоких и низких частот ЛАЧХ асимптотически приближаются к прямым, наклон которых составляет ± 20 дБ/дек (децибел на декаду), ±40 дБ/дек и т.д.
3. Могут быть нанесены на график несоизмеримые значения амплитуды и частоты.
Рассмотрим примеры:
1) Пусть 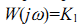 , тогда
, тогда 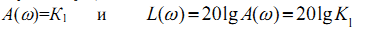
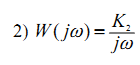
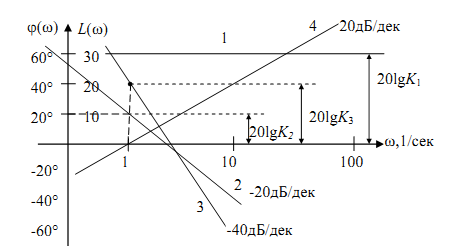
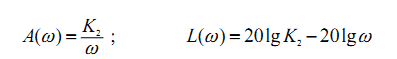 Тогда
Тогда
Если частота меняется в 10 раз (одна декада), то lg10=1 и мы имеем наклон характеристики в -20дБ/декада
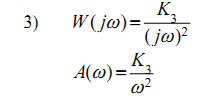
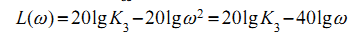
Наклон -40дБ/дек
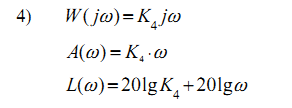
Наклон в этом случае равен +20дБ/дек
Перевод из дБ в разы (усиление равно сколько-то дБ, это будет в n раз):
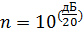
Например, если дБ=20, то n=101=1; если дБ=10, то n=100,5= 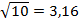
Дата добавления: 2016-01-30; просмотров: 6235;
