Расчет пространственных ферм

Расчет пространственных систем намного сложнее расчета плоских систем. Поэтому изучим только основы расчета ферм.

Кинематический анализ пространственной фермы проводится по формуле

W = 3n_У – n_C – ,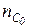

где n_У – число узлов фермы.

Требование W£0 является необходимым условием геометрической неизменяемости фермы. Для статической определимости необходимо выполнение условия W=0. Но, как известно, только количественного анализа еще недостаточно, следует проводить и качественный анализ. Для этого можно использовать принципы образования геометрически неизменяемых пространственных систем. Например, простейшим принципом является присоединение к телу триады (шарового шарнира с тремя связями). При его использовании вначале в ферме выделяют простейшее геометрически неизменяемое тело – треугольную пирамиду. Затем к нему последовательно присоединяют отдельные триады.

Геометрическую неизменяемость пространственной системы можно проверять и методом нулевой нагрузки: если при расчете системы без нагрузки усилия во всех стержнях и опорные реакции окажутся равными нулю, то система неизменяема, если же возникает неопределенность типа 0/0, система мгновенно изменяема.

Изучим два метода расчета пространственных ферм.

Метод сечений применяется при расчете ферм с простейшим образованием. Имеется два его варианта.

а) Метод вырезания узлов. Основан на последовательном вырезании узлов фермы, в которых число неизвестных усилий не более трех. Составляются три уравнения проекций SX=0, SY=0, SZ=0 на три оси. Эти оси не должны быть параллельными одной плоскости.

На этом методе основан признак определения нулевых стержней (стержней, усилия в которых равны нулю): если узел с тремя пересекающимися стержнями не нагружен, то усилия во всех трех стержнях равны нулю.

б) Метод моментной оси. Сущность метода: через ферму проводится сквозное сечение, затем составляется и решается уравнение момента относительно некоторой оси.

Ось, для которой составляется уравнение момента, называется моментной осью. Эта ось выбирается так, чтобы в уравнение вошла только одна неизвестная.

Метод разложения на плоские фермы. Когда стержни фермы располагаются группами на нескольких плоскостях, этот метод дает большой выигрыш в расчетах. Метод основан на следующей теореме: если силы, действующие на пространственную ферму, лежат в одной плоскости, то усилия во всех стержнях фермы, лежащих вне этой плоскости, равны нулю.

Порядок расчета фермы по этому методу состоит в следующем: внешняя нагрузка разлагается на несколько плоскостей; части фермы, лежащие в разных плоскостях, рассчитываются только на нагрузку в своей плоскости; затем применяется принцип суперпозиции.

Например, на следующую ферму (рис. 9.4 а) нагрузка действует только в двух плоскостях. Следовательно, ее расчет можно свести к расчету только двух плоских ферм (рис. 9.4 б, в). В стержнях фермы, лежащих на третьей плоскости (рис. 9.4 г), все усилия равны нулю.

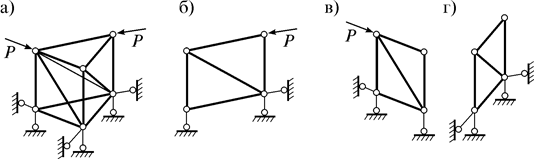
Рис. 9.4