Кинетическая и потенциальная энергии
Кинетическая энергия Wк механической системы - это энергия механического движения этой системы.
Сила 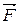 , действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа δА силы
, действуя на покоящееся тело и вызывая его движение, совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа δА силы 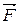 на пути, который тело прошло за время возрастания скорости от 0 до
на пути, который тело прошло за время возрастания скорости от 0 до 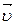 , идет на увеличение кинетической энергии dWк тела, т. е.
, идет на увеличение кинетической энергии dWк тела, т. е.
δА = dWк.
Используя второй закон Ньютона 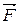 = m
= m 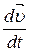 и умножая обе части равенства на перемещение
и умножая обе части равенства на перемещение 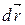 , получим
, получим
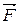
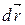 = m
= m 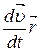 .
.
Так как 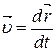 , то
, то
δA = m 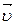 d
d 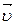 =mυdυ = dWк,
=mυdυ = dWк,
откуда
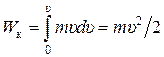 .
.
Таким образом, тело массой m, движущееся со скоростью υ, обладает кинетической энергией
Wк = mυ2/2 . (3.5)
Из формулы (3.4) видно, что кинетическая энергия зависит только от массы и скорости тела, т. е. кинетическая энергия системы есть функция состояния ее движения. При выводе формулы (3.4) предполагалось, что движение рассматривается в инерциальной системе отсчета, так как иначе нельзя было бы использовать законы Ньютона. В разных инерциальных системах отсчета, движущихся друг относительно друга, скорость тела, а следовательно, и его кинетическая энергия будут неодинаковы. Таким образом, кинетическая энергия зависит от выбора системы отсчета.
Потенциальная энергия Wp- механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Пусть взаимодействие тел осуществляется посредством силовых полей (например, поля упругих сил, поля гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит от того, по какой траектории это перемещение произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие в них, - консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной;ее примером является сила трения.
Тело, находясь в потенциальном поле сил, обладает потенциальной энергией Wp. Работа консервативных сил при элементарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:
δA = dWp. (3.6)
Работа δA выражается как скалярное произведение силы 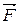 на перемещение
на перемещение 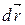 и выражение (3.6) можно записать в виде
и выражение (3.6) можно записать в виде
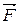
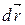 = - dWp. (3.7)
= - dWp. (3.7)
Следовательно, если известна функция Wp( 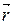 ), то из формулы (3.7) можно найти силу
), то из формулы (3.7) можно найти силу 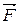 по модулю и направлению.
по модулю и направлению.
Потенциальная энергия может быть определена исходя из (3.7) как
Wp = 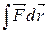 + C,
+ C,
где С - постоянная интегрирования, т. е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П по координатам. Поэтому потенциальную энергию тела в каком-то определенном положении считают равной нулю (выбирают нулевой уровень отсчета), а энергию тела в других положениях отсчитывают относительно нулевого уровня.
Для консервативных сил
Fx = - 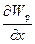 , Fy = -
, Fy = - 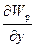 , Fz = -
, Fz = - 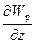 ,
,
или в векторном виде
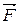 = - gradWp , (3.8)
= - gradWp , (3.8)
где
gradWp = 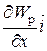 +
+ 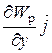 +
+ 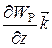 (3.9)
(3.9)
( 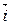 ,
, 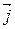 ,
, 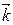 - единичные векторы координатных осей). Вектор, определяемый выражением (3.9), называется градиентом скаляра Wp.
- единичные векторы координатных осей). Вектор, определяемый выражением (3.9), называется градиентом скаляра Wp.
Для него наряду с обозначением gradWp применяется также обозначение 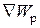 .
. 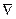 («на-бла») означает символический вектор, называемый оператором Гамильтона или набла-оператором:
(«на-бла») означает символический вектор, называемый оператором Гамильтона или набла-оператором:
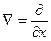
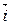 +
+ 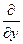
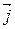 +
+ 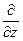
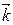 . (3.10)
. (3.10)
Конкретный вид функции Wp зависит от характера силового поля. Например, потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна
Wp = mgh, (3.11)
где высота h отсчитывается от нулевого уровня, для которого Wp = 0. Выражение (3.11) вытекает непосредственно из того, что потенциальная энергия равна работе силы тяжести при падении тела с высоты h на поверхность Земли.
Так как начало отсчета выбирается произвольно, то потенциальная энергия может иметь отрицательное значение (кинетическая энергия всегда положительна!). Если принять за нуль потенциальную энергию тела, лежащего на поверхности Земли, то потенциальная энергия тела, находящегося на дне шахты (глубина h'), Wp = - mgh'.
Найдем потенциальную энергию упругодеформированного тела (пружины). По третьему закону Ньютона, деформирующая сила Fx равна по модулю силе упругости Fx упр и противоположно ей направлена, т. е.
Fx = - Fx упр = kx.
Элементарная работа δA, совершаемая силой Fx при бесконечно малой деформации dx, равна
δA = Fx dx = kxdx,
а полная работа
A = 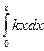 = kx2/2
= kx2/2
идет на увеличение потенциальной энергии пружины. Таким образом, потенциальная энергия упругодеформированного тела
Wp = kx2/2. (3.12)
Потенциальная энергия системы, подобно кинетической энергии, является функцией состояния системы. Она зависит только от конфигурации системы и ее положения по отношению к внешним телам.
Полная механическая энергия системы - энергия механического движения и взаимодействия:
W = Wк + Wp , (3.13)
т. е. равна сумме кинетической и потенциальной энергий.
Дата добавления: 2016-01-29; просмотров: 1331;
