Тема 1.4 Однофазные цепи переменного тока.
Электрическое поле
Любые физические тела содержат элементарные частицы, обладающие электрическим зарядом. Заряженные частицы всегда окружены электромагнитным полем и обладают определенной массой, энергией и другими свойствами, характерными для всех видов механического движения материи.
Электромагнитное поле - это особый вид материи, характеризуемый (в отличие от вещества) непрерывным распределением в пространстве и оказывающий силовое воздействие на электрически заряженные частицы или заряженные тела. Примером электромагнитного поля являются радиоволны, распространяющиеся в воздухе и пустоте со скоростью около 3 - 10s м/с.
Различают две физические стороны электромагнитного поля, проявление которых условно рассматривается как самостоятельное электрическое поле и магнитное поле.
Электрическим полем называют особое состояние материи, созданное элементарной материальной частицей, несущей электрические заряды, или каким-либо заряженным электричеством физическим телом в окружающей части пространства.
Электрическое поле проявляется в виде сил, действующей, на заряженные неподвижные частицы и тела. Оно может существовать в различных средах: вакууме, газах, жидкостях или твердых телах, причем возникающие при этом силы зависят от физических свойств среды. Электрическое поле, создаваемое неподвижными в пространстве и не изменяющимися во времени зарядами, называют электростатическим. Электрическое поле характеризуется величинами, используемыми в расчетах.
Интенсивность электрического поля характеризуется силой F его воздействия на единицу положительного заряда q0 и называется напряженностью этого поля (Н/кл)
ع = F/q0. (1.1)
Если напряженность электрического поля во всех точках одинакова, то оно будет равномерным.
Отношение работы А, совершаемой силами поля на перемещение заряда q0 из точки поля А в точку Б, к значению заряда называют электрическим напряж е н и е м:
UАБ = A/q0. (1-4)
Влияние среды на электрические силы характеризуется величиной εа, называемой абсолютной диэлектрической проницаемостью.
Частицы или тела, заряженные и имеющие одноименные заряды, отталкиваются, а разноименные - притягиваются.
Силы их взаимодействия определяются законом Кулона. Сила взаимодействия (притяжения или отталкивания) между двумя электрическими зарядами прямо пропорциональна произведению их значений и обратно пропорциональна квадрату расстояния между ними, а также абсолютной диэлектрической проницаемости среды:
F = q1q2/(4pl2εА )≈0,08 q1q2/l2εА (1.9)
где F — сила взаимодействия между зарядами, Н; q1q2— электрические заряды, Кл; l — расстояние между зарядами, м.
На рис. 1.1, а, б изображено электрическое поле двух разноименных зарядов. Пунктирными линиями показаны воображаемые силовые линии электрического поля. Принято считать, что силовые линии выходят из положительно заряженного тела и входят в отрицательно заряженное. В поле между двумя параллельными пластинами силовые линии представляют собой параллельные прямые. Такое поле является равномерным.
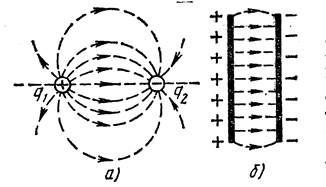
Рис.1.1. Электрическое поле двух разноименных зарядов:
а- поле двух шариков; б- поле между двумя параллейными пластинами
Важной характеристикой изоляционных материалов является также электрическая прочность.
Электрическая прочность есть предельная напряженность поля, которую диэлектрик способен выдерживать длительное время без нарушения его целости и потери изолирующих свойств. Электрическая прочность выражается в вольтах на метр (В/м). Превышение предельной напряженности дает разрушение диэлектрика или его пробой.
Тема 1.4 Однофазные цепи переменного тока.
Переменным называют ток (или напряжение), который изменяется периодически по направлению и непрерывно по значению. Промежуток времени, в течение которого происходит полный цикл изменения тока по величине и направлению, называется п е р и о д о м, а число периодов п секунду - частотой переменного тока
¦= 1/Т (4.1)
где ¦ - частота, Гц, Т- период, с.
В России для электрических сетей стандартная частота переменного тока, равная 50 Гц (50 периодов в секунду).
На рис. 4.2 дана схема получения синусоидальной э.д. с. (простейший генератор). Прямолинейный проводник вращается с постоянной частотой в равномерном магнитном поле. Положения, которые он занимает при перемещении вокруг неподвижного центра, обозначены цифрами 1-12:
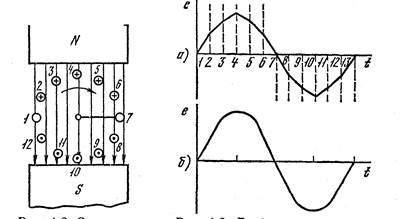
| Рис. 4.2. Схема получения переменной э.д.с. | Рис. 4.3. График изменения переменной э.д.с. |
Значения э.д.с. в каждый момент времени или при каждом положении проводника принято называть мгновенными значениями э.д.с. и обозначать е, например е1 ,е2 и т. д. Можно определить значения э. д. с. для каждого положения проводника
E = B l v sin a (4.2)
E = Em sin a (4.3)
Переменный угол а называют фазным или просто ф а з о й.
Между угловой скоростью и частотой существует зависимость:
w = 2p¦ = 2p/Т (4.4)
При синусоидальной э. д. с. ток и напряжение изменяются по аналогичному закону
I = Im sin wt (4.6)
u = Um sinwt. (4.7)
Амплитуды - наибольшие мгновенные значения, которые принимают переменные напряжения и токи. За один период напряжение и ток имеют два амплитудных значения: положи - тельное и отрицательное.
Действующим значением переменного синусоидального тока называют такое значение, которое численно равно значению постоянного тока, протекающего через то же сопротивление и вызывающего выделение такого же количества теплоты за равное время.
Между амплитудным Im и действующим значением переменного тока I существует следующее соотношение:
I = ImÖ2 = 0,707 I т. (4.9)
Для э. д. с. и напряжения соотношения аналогичны:
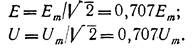
| (4.10) (4.11) |
Цепь переменного тока с активным сопротивлением. Под активным cопротив- лением проводника понимают такое сопротивление, в котором энергия выделяется в виде теплоты. Электрическая цепь обладает активным сопротивлением R, индуктивностью L и емкостью С, которые являются ее параметрами.
Рассмотрим электрическую цепь переменного тока, в которую включено только активное сопротивление (рис.4.6, а):
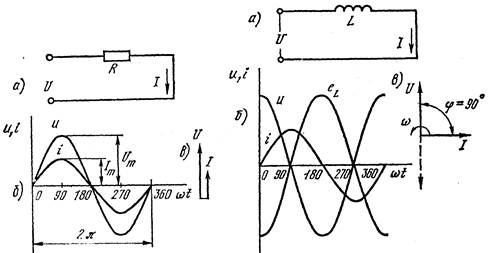
| Рис. 4.6. Цепь с активным сопротивлением: а - схема; б - кривые тока и напряжения цепи; в - векторная диаграмма | Рис. 4.7. Цепь с индуктивностью: а - схема; б - кривые тока, напряжения и э. д. с. цепи; в - векторная диаграмма |
К этой цепи подведено переменное напряжение, изменяющееся по закону и =Um sin wt.
Для определения мгновенного значения тока в цепи воспользуемся законом Ома
i = U/R = Um sin wt / R = Im sin wt (4.12)
Амплитудное значение тока
Im = Um / R (4.13)
Из выражения (4.12) следует, что изменение тока по времени точно совпадает с изменением напряжения; максимумы и минимумы этих величин наступают одновременно. Такие величины называют совпадающими по фазе.
Выражение для действующего значения тока
I = U/R. (4.14)
Цепь переменного тока с индуктивностью. Рассмотрим теперь цепь, обладающую только индуктивностью L. Она реально не существует, так как любая катушка обязательно содержит и активное сопротивление. Однако для уяснения физической стороны процесса исследуем катушку, лишенную активного сопротивления (рис. 4.7, а).
Известно, что eL = -L di/ dt.
Следовательно, u=L di/ dt
Для максимальных значений напряжения и тока получим следующее выражение:
Um = Im wL. (4.16)
Для действующих значений
U = I w L (4.17)
или
I = U/(wL) = U/XL. (4.18)
Эта формула выражает закон Ома для цепи переменного тока с индуктивностью. Значение XL=wL=2pfL называют индуктивным сопротивлением. Легко показать, что XL выражается, как и активное сопротивление, в омах: XL = 1/с* Гн = 1/с* Ом*с = Ом.
В цепи с индуктивностью ток отстает по фазе от напряжения на четверть периода (во времени), а в угловой мере - на 90° (p/2).
Цепь переменного тока с емкостью. Рассмотрим цепь, в которую включен конденсатор с емкостью С; предположим, что конденсатор не имеет активного сопротивления (рис. 4.8, а):
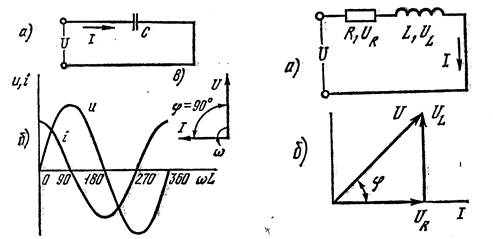
| Рис. 4.8. Цепь с емкостью: а - схема; б - кривые тока и напряжения цепи; в - векторная диаграмма | Рис. 4.9. Цепь с активным и индуктивным сопротивлениями: а - схема; б - векторная диаграмма |
При включении конденсатора в цепь переменного тока происходит непрерывный процесс перезарядки конденсатора с изменением два раза в течение периода знака заряда обкладок с плюса на минус и наоборот. В результате этого по цепи непрерывно движутся заряды, т. е. протекает переменный ток, называемый емкостным.
Закон изменения тока будет иметь следующее выражение:
i = Uт w С cos wt (4.19)
Для действующих значений I = U w С, или
I = U/ [1/(wС)], (4.20)
где 1/ (wС) - емкостное сопротивление Хс :
Хс = 1/(wС) = 1/(2p¦С). (4.20а)
Формула (4.20) выражает закон Ома для цепи с емкостью.
На рис. 4.8, б показаны кривые изменения напряжения и тока для такой цепи и векторная диаграмма. В отличие от цепи с индуктивностью ток в данном случае по фазе опережает напряжение на 1/4 периода (p/2).
Цепь переменного тока с активным сопротивлением и индуктивностью. Рассмотрим приведенную на рис. 4.9, а цепь с реальной катушкой, имеющей активное и индуктивное сопротивления. Для такой цепи уравнение второго закона Кирхгофа для мгновенных значений тока и напряжения запишем следующим образом: u + eL = iR; и = -Ldi/dt.
или u = iR+Ldi/ dt = uR + uL. (4.21)
Следовательно, в данном случае имеет место последовательное соединение L и R и напряжение, приложенное к катушке, состоит из двух слагаемых:
падения напряжения в активном сопротивлении
uR = i R (4.22)
и напряжения
ul = Ldi/ dt (4.23)
уравновешивающего э. д. с. самоиндукции.
Из изложенного следует, что вектор падения напряжения совпадает по направлению с вектором тока, а вектор UL опережает его на 90о. Сложив геометрически векторы, получаем вектор напряжения U (см. векторную диаграмму на рис. 4.9, б). Таким образом, в цепи с реальной катушкой ток тоже отстает от напряжения, но на угол φ, меньший 90°.
Если в полученном на векторной диаграмме треугольнике напряжений разделить значения сторон на ток I, то получим треугольник сопротивлений (рис. 4.10), катеты которого равны активному R и индуктивному XL сопротивлениям, а гипотенуза
Z =ÖR2+XL2 (4.24)
Z называют полным сопротивлением цепи. Угол сдвига фаз j определяется из следующих соотношений:
tg j= XL/R (4.25)
cos j = R/Z (4.26)
sin j = XL/Z (4.27)
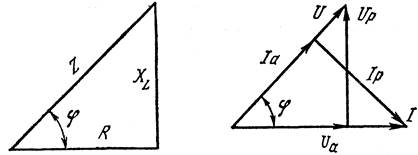
| Рис. 4.10. Треугольник сопротивлений | Рис. 4.11. Треугольники токов и напряжений |
Из треугольника напряжений вытекают следующие соотношения:
UR =U соs j (4.28)
UL = U sin j (4.28а)
Проекция вектора напряжения на вектор тока называется активной составляющей вектора напряжения и обозначается Uа. Проекция вектора напряжения на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается Uр, в данном случае Uр = UL. По аналогии, вектор тока можно разложить на активную и реактивную составляющие, что видно из рис. 4.11 (треугольник токов):
Ia = I cos j (4.29)
Ip = I sin j (4.30)
I = ÖIa2 + Iр2 (4.30а)
Проекцию вектора общего тока на вектор приложенного напряжения называют активной составляющей тока (Iа), а проекцию вектора общего тока на направление, перпендику- лярное вектору приложенного напряжения, - реактивной составляющейтока(Iр) 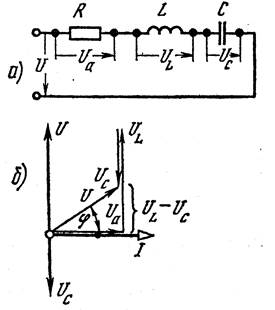
Рис. 4.12. Последовательное соединение: а - схема; б - векторная диаграмма
Последовательная цепь переменного тока с активным сопротивлением, индуктивностью и емкостью. На рис. 4.12 представлена цепь переменного тока, обладающая активным сопротивлением R (резистор), индуктивностью L (катушка) и емкостью С (конденсатор). В такой цепи приложенное напряжение состоит из трех слагаемых - активной, индуктивной и емкостной:
u = uа + uL + uс,
Для действующих значений суммирование слагающих должно производиться геометрически: U = Ua + UL, + Uc. Отдельные составляющие действующих значений напряжения согласно закону Ома следующие: Ua=IR; UL=IXL; UC=IXC.
Из построенной на рис. 4.12 векторной диаграммы следует, что действующее значение приложенного напряжения
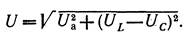 (4.31)
(4.31)
Подставив значения составляющих, получаем
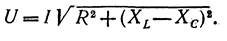 (4.32)
(4.32)
Отсюда
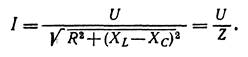 (4.33)
(4.33)
Полученное выражение является формулой закона Ома для цепи переменного тока, в которой знаменатель выражает полное сопротивление неразветвленной цепи переменного тока:
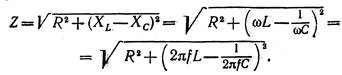 (4.34)
(4.34)
Резонанс напряжений.Как видно из выражения (4.33), при XL-Xс общий ток в цепи определяется только активным сопротивлением (XL - Хс = 0) и имеет наибольшее значение. В такой цепи имеет место резонанс напряжений. При этом напряжения UL=UC направлены в противоположные стороны и компенсируют друг друга. Однако при небольших значениях R, UL и Uc каждое может быть значительным, что может привести к пробою изоляции индуктивной катушки и конденсатора. При резонансе напряжений wL = 1/(wC), откуда
wp = l/ÖLC (4.35)
Величину wр называют угловой резонансной частотой, и зависит она только от величин индуктивности и емкости цепи. Резонансная частота цепи (собственная частота)
¦р = 1/(2pÖLC). (4.36)
При резонансе напряжений энергии полей магнитного WM = LI2/2 и электрического Wэ=CU2/2 равны и взаимно передаются от катушки к конденсатору при колебаниях тока и напряжения без потребления энергии от источника, т. е. возникают незатухающие колебания. Энергия источника, питающего цепь, расходуется только на выделение теплоты в активном сопротивлении.
Векторная диаграмма при резонансе напряжений приведена на рис. 4.13. Следует иметь в виду, что явление резонанса имеет место при равенстве собственной частоты колебательного контура с частотой источника переменного тока.
К о л ебательным контуром называют электрическую цепь, содержащую емкость и индуктивность, в которой возникают колебания тока и напряжения. Явление резонанса напряжения используется в технике, связи и радиотехнике для настройки цепи на определенную частоту. В электроэнергетических установках (линиях электропередачи) резонанс напряжений - явление вредное, так как возникают перенапряжения, опасные для изоляции установок.
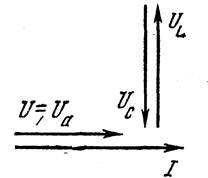
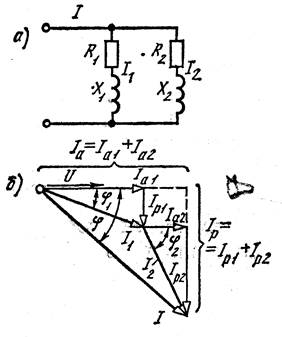
Параллельная цепь переменного тока. На рис. 4.14 показана цепь переменного тока, состоящая из двух катушек, соединенных параллельно, обладающих активными R1 и R2 и индуктивными Х1 и Х2 сопротивлениям. Нетрудно увидеть, что на зажимах катушек напряжение U будет одинаковым (сопротивлением соединительных проводов пренебрегаем). Ток в первой параллельной ветви согласно закону Ома I1 = U/Z1 = U/ÖR12+X12, а во второй
I2 = U/Z2 = U/ÖR22 +X22
Эти токи отстают по фазе от напряжения на углы сдвига фаз j1 и j2, причем tg j1 = X1/R1 и
tg j2 = X2/R2. Токи I1 и I2 можно разложить на активную и реактивную составляющие: Ia1= I1 cos j1 и Ip1 = I1 sin j1; Ia2 = I2 cosj2 и Ip2 = I2 sinj2.
| 
|
| Рис. 4.13. Векторная диаграмма при резонансе напряжений | Рис. 4.14. Параллельное соединение двух катушек: а - схема; б - векторная диаграмма |
Сумма активных составляющих токов ветвей, совпадающих по фазе, равна активной составляющей общего тока:
Iа = Ia1+Ia2 (4.43)
Сумма реактивных составляющих токов ветвей равна реактивной составляющей общего тока:
Ip = Ip1 + Ip2 (4.44)
Общий ток, протекающий в неразветвленной части цепи,
I = ÖIa2 + Iр2 (4.45)
Этот ток отстает по фазе от приложенного напряжения на угол j, причем
tg j = Ip/Ia (4.46)
cos j = Iа/I (4.47)
sin j = Ip/I (4.48)
Разветвленная цепь состоит из соединенных параллельно индуктивности и емкости (рис. 4.15), в такой цепи при wL = l/(wC) возникает явление резонанса токов, при котором токи в ветвях 1L и Iс равны между собой и могут значительно превышать общий ток I, протекающий в неразветвленной части цепи. Условия появления резонанса токов аналогичны ранее изложенным для случая резонанса напряжений. При резонансе токов вся энергия, подводимая к цепи, расходуется на выделение теплоты в активном сопротивлении цепи, а между индуктивностью и емкостью происходит колебательный обмен запасенной энергией.
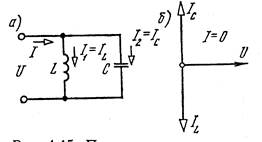
Рис. 4.15. Параллельное соединение катушки и конденсатора:
а - схема; б – векторная диаграмма
В отличие от резонанса напряжений резонанс токов не представляет опасности. Он возникает, когда в цепь включены мощные конденсаторные батареи и реактивные катушки, что учитывается при расчете сети и не является неожиданным.
Работа и мощность в цепи переменного тока. Мощность, потребляемая в цепи, равна произведению напряжения на ее зажимах и силы тока. При переменном токе это справедливо только для мгновенных значений мощности: р = u i.
В цепях, обладающих кроме активного сопротивления индуктивностью и емкостью, т. е. реактивными сопротивлениями, имеет место сдвиг фаз между током и напряжением, поэтому активная мощность, развиваемая переменным током в таких цепях, меньше произведения UI:
Р = U I cos j (4.49)
Величину cos j принято называть коэффициентом мощности.
В теории переменного тока помимо активной мощности, выражаемой в ваттах (Вт) и киловаттах (кВт), пользуются еще понятиями реактивной мощности Q [ВАр] и полной S [ВА]:
Q = U I sin j (4.49)
S = U I (4.51)
На основании формул (4.49) - (4.51) легко построить графическое изображение треугольника мощностей (рис. 4.17), гипотенуза которого:
S = ÖР2+ Q2 (4.52)
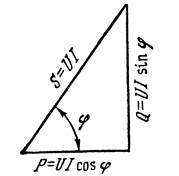
Рис. 4.17. Треугольник мощностей
Активная мощность
Р = UI cos j = Р=UIа. (4.53)
т. е. мощность равна произведению действующих значений напряжения и активной составляющей тока. Соответственно реактивная мощность равна произведению действующих значений напряжения и реактивной составляющей тока:
Q = Р = UI sin j = UIр. (4.54)
Активная мощность характеризует преобразование электрической энергии в другие виды (теплоту, механическую работу).
Реактивная мощность характеризует колебания электрической энергии между генератором и электроприемником, обусловленные переменными электрическим и магнитным полями.
ЛЕКЦИЯ 2
Дата добавления: 2016-01-20; просмотров: 9628;
