Энергетический фильтр.

Энергетический фильтр строится на основе критерия максимума энергетического отношения сигнал/помеха на выходе фильтра и предназначен для решения задачи выделения сигнала, обладающего наибольшей энергией или дисперсией. В этом отношении следует подчеркнуть его аналогию с методом главных компонент.

Математическая модель поля для энергетического фильтра совпадает с моделью для фильтра Колмогорова-Винера, т.е. сигнал и помеха представлены стационарными случайными процессами с заданными АКФ.

Энергетический фильтр занимает промежуточное положение между фильтром воспроизведения Колмогорова-Винера и согласованным фильтром, поскольку он строится как фильтр обнаружения, так как максимизируется отношение сигнал/помеха, а решает задачу выделения сигнала, т.е. задачу оценки формы наиболее энергоемкого сигнала. Оценка формы сигнала оказывается возможной по причине максимизации энергетического, а не пикового отношения, т.е. отношения по интервалу, определяемого длиной фильтра, а не в одной, центральной точке.

Энергетическое отношение сигнал/помеха на выходе фильтра определяется в виде:

(7.17) ,

где 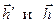- соответственно вектор-строка и вектор-столбец весовых коэффициентов фильтра, - корреляционные матрицы сигнала и помехи, построенные по их заданным АКФ.

Дифференцирование 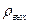по 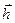в (7.17) и приравнивание производной к нулю приводит к системе линейных уравнений в матричной форме

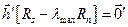(7.18)

где 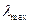- есть энергетическое отношение сигнал/помеха, т.е. . В то же время 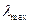является максимальным собственным значением разностной матрицы 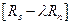, а при этом представляет значения собственного вектора, соответствующего 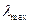. Неопределенность решения уравнения (7.18), связанная с равенством правой части нулю, снимается путем нормировки весовых коэффициентов .

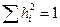Из рассмотрения энергетического фильтра раскрывается физический смысл максимального собственного значения 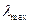, представляющего не что иное, как энергетическое отношение сигнал/помеха на выходе фильтра.

Профильтрованный сигнал на выходе фильтра 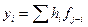с весовой функцией, представленной собственным вектором, соответствующим 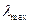, является первой главной компонентой в методе главных компонент. Физический смысл 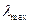позволяет считать, что выходной сигнал обеспечивает выделение составляющей наблюденного поля, обладающей наибольшей энергией.

В модели поля 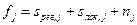такой составляющей оказывается региональный тренд, а в модели - локальная составляющая.

Пример 3. Пусть сигнал и помеха заданы теми же значениями, что и в примерах 1 и 2, т.е. 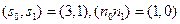. Их автокорреляции 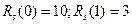; 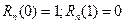. Найдем весовые коэффициенты энергетического фильтра и по ним определим пиковое и энергетическое отношения сигнал/помеха на выходе фильтра.

Составим матричное уравнение (7.18):

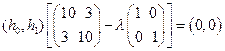
Определитель матрицы, заключенный в квадратные скобки, равен

.

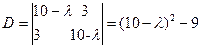Путем приравнивания определителя к нулю, получаем:

.

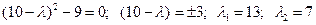Подставим 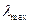=13 в исходное уравнение 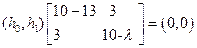, что приводит к уравнениям: 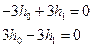т.е.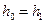

Из нормировки весовых коэффициентов при 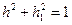, получаем .

Значения профильтрованного сигнала будут равны

.

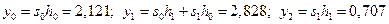Рассчитаем пиковое и энергетическое отношения сигнал/помеха на выходе фильтра: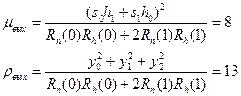

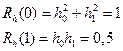
Отсюда следует, что , и энергетическое отношение больше пикового.

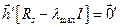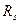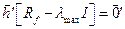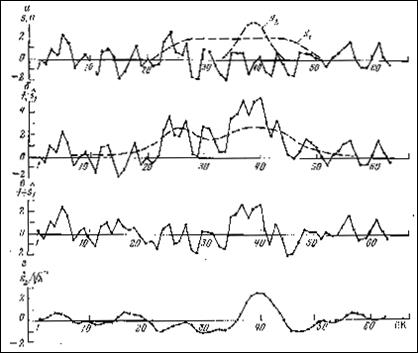
Задача нахождения весовой функции энергетического фильтра упрощается, если помеха является некоррелированной. Тогда уравнение (7.18) запишется, как . Это приводит к тому, что при слабых помехах вместо можно использовать АКФ наблюденного поля, т.е. , т.е. весовая функция определяется без привлечения априорной информации о сигнале и помехи. Результаты выделения и оценки формы двух сигналов разной энергии с помощью энергетического фильтра приводятся на рис.7.2.

Рис.7.2. Результаты выделения и оценки формы двух сигналов разной энергии с помощью энергетического фильтра. а - сигналы s1 и s2 с различной энергией и некоррелированная помеха, б - сигнал на входе фильтра, в - разность между входным сигналом и результатом фильтрации, г - результат энергетической фильтрации значение рис.в.

Относительно реализации оптимальных линейных фильтров следует сделать следующие замечания:

Замечание 1. Согласованный фильтр, обеспечивающий обнаружение заданного по форме сигнала, аналогичен вейвлет-анализу, в котором согласованная фильтрация осуществляется многократно для каждой копии порождающего вейвлета. Решение о наличии сигнала конкретной формы принимается по максимальной величине выходного, т.е. профильтрованного сигнала. Разложение входного сигнала по всем копиям порождающего вейвлета аналогично Фурье-анализу, что позволяет рассчитать общую энергию (дисперсию) этих составляющих. Последнее обстоятельство используется при оценке AVO-эффекта, сопровождающего залежи углеводородов.

Замечание 2. Двумерные оптимальные фильтры реализуются как двумерные линейные фильтры, для которых весовые функции рассчитываются по блочным корреляционным матрицам. Построение этих матриц производится по двумерным АКФ сигнала и помех. .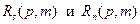

Например, система уравнений двумерного согласованного фильтра для нахождения весовой функции 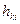будет записана в виде .

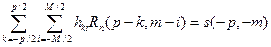Поскольку реализация двумерных оптимальных фильтров трудоемка даже для современных персональных компьютеров, то двумерную АКФ стараются представить в виде произведения одномерных АКФ, полученных раздельно по x и по y (по х и по t). Это позволяет двумерную фильтрацию свести к раздельно реализуемой фильтрации по координате x для каждого профиля и по координате y, т.е. между профилями.

Другое упрощение состоит в аппроксимации двумерных спектров сигналов и помех изотропными спектрами в предположении о центральной осевой симметрии исходного поля, т.е. когда можно осуществить замену 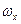и на частоту .

Наконец, при некоррелированности помехи между профилями (трассами) осуществляется оптимальная фильтрация лишь по одной координате (x или по t), а затем по результатам фильтрации проводится суммирование в пределах скользящего окна, включающего N профилей (трасс) по заданному направлению сигнала.

Замечание 3. Трехмерные линейные неоптимальные и оптимальные фильтры приобретают в настоящее время все большее значение в связи с обработкой данных 3D-сейсморазведки и 3D-электроразведки. Для потенциальных полей трехмерные массивы данных образуются путем пересчета данных по площади в нижнее полупространство.