Установившееся и неустановившееся движение.

Установившимся называют такое движение жидкости, при ко­тором скорость потока и давление в любой его точке не изменяются с течением времени и зависят только от ее положения в потоке, т. е. являются функциями ее координат. Примерами установившегося движения могут служить истечение жидкости из отверстия резервуара при постоянном напоре, а также поток воды в канале при не­изменном его сечении и постоянной глубине.

Неустановившимся называют такое движение жидкости, при ко­тором скорость движения и давление в каждой данной точке изме­няются с течением времени, т. е. являются функциями не только координат, но и времени. Примером неустановившегося движения служит истечении жидкости из отверстия резервуара при перемен­ном напоре. В этом случае в каждой точке сечения струи, выте­кающей из отверстия, скорость движения и давление изменяются во времени.

Линия тока. В точках 1, 2, 3 и т. д. потока, взятых на расстоя­нии ΔS друг от друга, проведем векторы u₁, u₂, u₃, показывающие значение и направление скоростей движения частиц жидкости в данный момент времени (рис. 1.18). Получим ломаную линию 1—2— 3и т. д. Если уменьшить длину от­резков ΔS, то в пределе ломаная линия станет кривой.

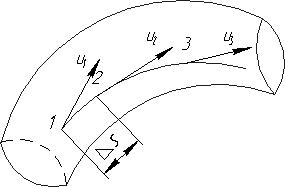
Рис. 1.18. Схематическое изображение линии тока в потоке

Эта кривая, называемая линией тока, характеризуется тем, что в данный момент времени во всех ее точках векторы скоростей бу­дут касательными к ней.

Элементарная струнка. Если в движущейся жидкости выделить бесконечно малый замкнутый контур и через все его точки провести линии тока, соответствующие данному моменту времени, получится как бы трубчатая непроницаемая поверхность, называемая трубкой тока.

Масса жидкости, движущейся внутри трубки тока, образует элементарную струйку.

Поток. Совокупность элементарных струек, представляющая собой непрерывную массу частиц, движущихся но какому-либо направлению, образует поток жидкости. Поток может быть пол­ностью или частично ограничен твердыми стенками, например в трубопроводе или канале, и может быть свободным, например струя, выходящая из сопла гидромонитора.

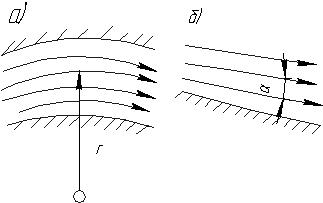
Рис. 1.19. Условия плавно из­меняющегося движения

Равномерным называют такое уста­новившееся движение жидкости, при котором живые сечения и средняя скорость потока не меняются по его длине. Примером равномерного дви­жения служит движение жидкости в цилиндрической трубе или в кана­ле неизменного сечения и постоянной глубины.

Неравномерным называют такое установившееся движение жид­кости, при котором живые сечения и средние скорости потока из­меняются по его длине. Примером неравномерного движения служит движение жидкости в конической трубе, в естественном русле, на перепаде.

При равномерном движении липни тока представляют собой систему прямых параллельных линий. Такое движение называется также параллельно–струйным. При движении жидкости в естествен­ных руслах живое сечение обычно непрерывно изменяется вдоль по­тока как по форме, так и по площади, и движение жидкости являет­ся установившимся неравномерным. Для облегчения изучения та­кого движения в гидравлике введено понятие плавно изменяюще­гося движения, которое характеризуется следующими свойствами (рис. 1.19):

Последнее свойство просто обосновывается. Если внутри плавно изменяющегося потока выделить частицу жидкости и спроекти­ровать все действующие на нее силы па плоскость живого сечения, то вследствие того, что скорости и ускорения почти перпендикуляр­ны живому сечению, силы инерции в уравнение равновесия не войдут; в связи с этим уравнение равновесия и закон распределения давления в плоскости живого сечения не будут отличаться от закона распределения давления в жидкости, находящейся в покое.

Напорным называется поток, у которого но всему периметру живого сечения жидкость соприкасается с твердыми стенками. Примером напорного потока может служить движение воды в водо­проводных трубах.

Безнапорным называется поток со свободной поверхностью. Примером безнапорного потока служит движение воды в реках, каналах и канализационных трубах.

1. В механике сплошной среды применяются два метода исследования – метод Л. Эйлера и метод Лагранжа.

В методе Л.Эйлера рассчитываются параметры сплошной среды в одних и тех же неподвижных точках пространства. Этот метод чаще всего используется в гидромеханике. Здесь данные расчета легко сравнивать с результатами экспериментов, т.к. все датчики (давления, температуры, скорости и т.п.) устанавливаются в неподвижных точках (труб, воздуховодов и т.п.).

В методе Лагранжа рассчитываются параметры (скорость, давление, температура) в одних и тех же подвижных точках среды. Метод Лагранжа более сложный. Он используется в научных исследованиях и в теории упругости. Здесь рассчитываются траектории частиц, т.к. здесь важно рассчитать перемещение точек тела. Здесь датчики параметров перемещаются вместе с точками твердого тела.