РАВНОВЕСИЕ ЖИДКОСТИ ВО ВРАЩАЮЩЕМСЯ СОСУДЕ (ОТНОСИТЕЛЬНЫЙ ПОКОЙ ЖИДКОСТИ)

Рассмотрим случай, когда на жидкость, помимо объемных сил тяжести, действует еще другая система объемных сил, например, система центробежных сил инерции.

Возьмем круглоцилиндрический сосуд, наполненный жидкостью, причем будем считать, что этот сосуд вращается вокруг своей вертикальной оси равномерно, т. е. с постоянной угловой скоростью (рис. 2-14). Благодаря силам трения стенки вращающегося сосуда будут вначале увлекать за собой жидкость, а по истечении некоторого времени вся жидкость начнет вращаться вместе с сосудом с той же угловой скоростью Ω, находясь по отношению к стенкам сосуда в покое. Силы трения при этом внутри жидкости, а также между жидкостью, стенками сосуда и его дном, будут отсутствовать.

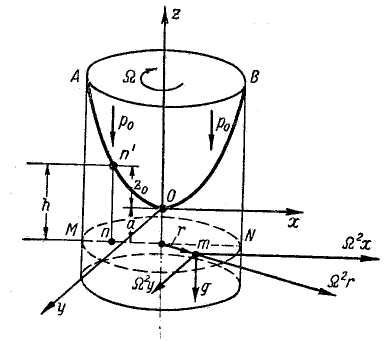
Рис. 2-14. Цилиндрический сосуд, вращающийся относительно вертикальной оси Oz

АОВ — свободная поверхность жидкости

Если оси координат, расположенные, как показано на чертеже, будем считать скрепленными с вращающимся сосудом, то по отношению к таким вращающимся осям координат жидкость также будет находиться в покое. Поэтому для исследования вращающейся жидкости при указанных подвижных осях координат могут быть применены известные уравнения Эйлера (2-14).

В эти уравнения входит объемная сила 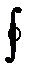, действующая на единицу массы жидкости. В данном случае сила 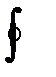будет слагаться из двух сил: силы тяжести и центробежной силы.

С тем чтобы найти проекцию центробежной силы на оси координат, наметим внутри жидкости точку т и выделим у нее элементарную массу жидкости δM. Масса δM будет вращаться вокруг оси сосуда, двигаясь по окружности, имеющей радиус r и лежащей в плоскости, нормальной к оси сосуда. Центробежная сила, действующая на данную массу, будет

I’= 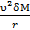, (2-62)

где υ - скорость движения массы δM по окружности радиуса r.

Центробежная сила, отнесенная к единице массы жидкости, сосредоточенной в точке т,

I = 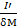= Ω²r. (2-63)

Эта сила, так же как и сила I’, направлена по радиусу от оси сосуда наружу. Проекции силы I (отнесенной к единице м- ассы) на оси координат

I_x = Ω²rcos(r,x) = Ω²_x

I_y = Ω²rcos(r,y) = Ω²_y

I_z = 0 (2-64)

Проекции объемной силы тяжести, отнесенной к единице массы, выражаются зависимостью (2-28). Складывая объемные силы тяжести и объемные центробежные силы, отнесенные к единице массы, получаем

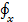= 0 +Ω²x = Ω²x;

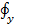= 0 + Ω²y = Ω²y;

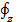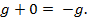= - (2-65)

Подставляя (2-65) в (2-17), найдем

dp_A = ρ(Ω²xdx + Ω²ydy – 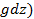, (2-66)

что после интегрирования дает

dp_A = ρ( 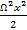+ 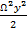– 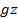) + C = 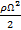(x² + y²) – ρ 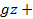C. (2-67)

Постоянную интегрирования С устанавливаем, написав (2-67) применительно к точке, находящейся в начале координат, для которой x = y = z =0; p = p₀. Как видно,

C = p₀ (2-68)

причем (2-67) перепишется в виде:

p_A = p₀ + 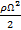(x₂ +y₂) - γz (2-69)

Это последнее уравнение и выражает закон распределения давления в рассматриваемой жидкости. Пользуясь таким уравнением, можно найти поверхности равного давления.

Действительно, уравнение поверхности, во всех точках которой давление p_A = p_i= const, запишется в виде

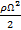(x₂ +y₂) – γz = p_i – p₀. (2-70)

Уравнение (2-70) выражает поверхность, являющуюся параболоидом вращения (с вертикальной осью).

Свободная поверхность жидкости, характеризуемая постоянным давлением p_i = p₀, представляет собой также параболоид вращения; уравнение ее будет:

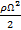(x₂ +y₂) – γz = 0. (2-71)

Если учесть, что x² + y² = r², то, решив (2-71) относительно z, получим следующее уравнение, по которому легко построить параболу АОВ, дающую свободную поверхность:

z₀ = 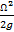r² (2-72)

где z₀- ордината кривой АОВ.

Распределение давления в горизонтальной плоскости MN, лежащей ниже начала координат на величину a, можно найти, пользуясь (2-69):

p_A = p₀ + 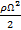(x² +y²) +γa = p₀ + ρ 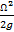r²+ γa = p₀ + γ( 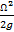r²+ a). (2-73)

Учитывая (2-72), получаем

p_A = p₀ + γ(a + z₀) = p₀ + γh (2-74)

где h = a +z₀ показано на рис. 2-14.

Таким образом, давление в жидкости, находящейся внутри равномерно вращающегося сосуда, выражается зависимостью того же вида, что и для случая тяжелой покоящейся жидкости [см. (2-39)]; под величиной h здесь надо понимать только заглубление рассматриваемой точки под криволинейной свободной поверхностью.