Структурные средние величины
Структурные (позиционные) средние – это средние величины, которые занимают определенное место (позицию) в ранжированном вариационном ряду.
Мода(Mo) - это значение признака, наиболее часто встречающееся в исследуемой совокупности.
Для дискретных вариационных рядов модой будет значение варианты с наибольшей частотой
Пример. Определить моду по имеющимся данным (табл. 7.5).
Таблица 7.5 – Распределение женской обуви, проданной в обувном магазине N, февраль 2013 г.
| Размер обуви | Число купленных пар |
| Итого |
По данным табл. 5 видно, что наибольшая частота fmax = 28, ей соответствует значение признака x = 37 размер. Следовательно, Mo = 37 размер обуви, т.е. именно этот размер обуви пользовался наибольшим спросом, наиболее часто покупали обувь 37-го размера.
В интервальном вариационном ряду сначала определяется модальный интервал, т.е. содержащий моду – интервал с наибольшей частотой (в случае интервального распределения с равными интервалами, в случае с неравными интервалами – по наибольшей плотности).
Модой приближенно считается середина модального интервала. Конкретное значение моды для интервального ряда определяется по формуле:
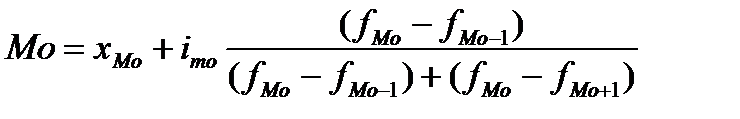 ,
,
где xMo – нижняя граница модального интервала;
iMo – величина модального интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.
Пример. Определить моду по имеющимся данным (табл. 7.6).
Таблица 7.6 – Распределение работников по стажу
| Стаж, лет | Число работников, чел. |
| до 2 2-4 4-6 6-8 8-10 свыше 10 | |
| Итого |
По данным табл. 6 видно, что наибольшая частота fmax = 35, ей соответствует интервал: 6-8 лет (модальный интервал). Определим моду по формуле:
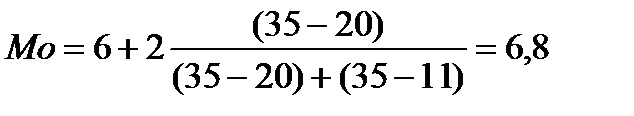 лет.
лет.
Следовательно, Mo = 6,8 лет, т.е. большинство работников имеют стаж 6,8 лет.
Название медианы взято из геометрии, где им именуется отрезок, соединяющий одну из вершин треугольника с серединой противоположной стороны и разделяющий, таким образом, сторону треугольника на две равные части.
Медиана(Mе) – это значение признака, приходящееся на середину ранжированной совокупности. Иначе медиана – это величина, которая делит численность упорядоченного вариационного ряда на две равные части – одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие.
Для ранжированного ряда (т.е.упорядоченного - построенного в порядке возрастания или убывания индивидуальных значений признака) с нечетным числом членов (n=нечет) медианой является варианта, расположенная в центре ряда. Порядковый номер медианы (NMe) определяется следующим образом:
NMe=(n+1)/2.
Пример. В ряду из 51 члена номер медианы (51+1)/2 = 26, т.е. медианой является вариант, стоящий в ряду 26-ым по порядку.
Дляранжированного ряда с четным числом членов (n=чет) – медианой будет средняя арифметическая из двух значений признака, расположенных в середине ряда. Порядковые номера двух центральных вариант определяются следующим образом:
NMe1=n/2; NMe2=(n/2)+1.
Пример. При n=50; NMe1 = 50/2 = 25; NMe2 = (50/2)+1 = 26, т.е. медианой является средняя из вариант, стоящих в ряду 25-ой и 26-ой по порядку.
В дискретных вариационных рядах медиана находится по накопленной частоте, соответствующей порядковому номеру медианы или впервые его превышающей. Иначе по накопленной частоте равной или впервые превышающей половину суммы всех частот ряда.
Пример. Определить медиану по имеющимся данным (табл. 7.7).
Таблица 7.7 – Распределение женской обуви, проданной в обувном магазине N, февраль 2013 г.
| Размер обуви | Число купленных пар | Накопленные частоты | % к итогу |
| Итого | х | х |
По данным табл. 7 определим порядковый номер медианы: NMe=(67+1)/2=34. Накопленная частота, впервые превышающая это значение, S = 41, ей соответствует значение признака x = 37 размер. Следовательно, Me = 37 размер обуви, т.е. половина пар покупается меньше 37-го размера, а другая половина – больше.
В этом примере мода и медиана совпадают, но они могут и не совпадать.
В интервальном вариационном ряду определяются накопленные частоты, по данным о накопленных частотах находят медианный интервал – интервал, в котором накопленная частота составляет половину или впервые превышает половину всей суммы частот. Формула для определения медианы в интервальном ряду распределения имеет следующий вид:
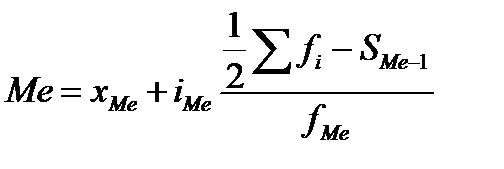 .
.
где xMe – нижняя граница медианного интервала;
iMe – величина медианного интервала;
∑fi – сумма частот ряда;
SMe-1 – сумма накопленных частот интервала, предшествующего медианному;
fMe – частота медианного интервала.
Пример. Определить медиану по имеющимся данным (табл. 7.8).
Таблица 7.8 – Распределение работников по стажу
| Стаж, лет | Число работников, чел. | Накопленные частоты |
| до 2 2-4 4-6 6-8 8-10 свыше 10 | ||
| Итого | х |
По данным табл. 8 определим порядковый номер медианы: NMe=100/2=50. Накопленная частота, впервые превышающая это значение, S = 82, ей соответствует интервал 6-8 лет (медианный интервал). В этом примере модальный и медианный интервал совпадают, но они могут и не совпадать. Определим медиану по формуле:
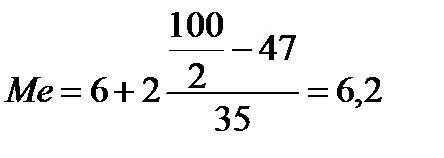 лет
лет
Следовательно, Me = 6,2 года, т.е. половина работников имеют стаж менее 6,2 года, а другая половина – более.
Мода и медиана находят широкое применение в разных областях экономики. Так, исчисление модальной производительности труда, модальной себестоимости и т.д. дает возможность экономисту судить о преобладающем в данный момент их уровне. Эта характеристика должна быть использована для выявления резервов нашей экономики. Мода имеет значение для решения практических задач. Так, при планировании массового выпуска одежды и обуви устанавливается размер продукции, который пользуется наибольшим спросом (модальный размер). Мода может быть использована в качестве приближенной характеристики уровня изучаемого признака вместо средней арифметической, если распределения частот близко к симметричному и имеет одну неплоскую вершину.
Медиану следует применять в качестве средней величины в тех случаях, где нет достаточной уверенности в однородности изучаемой совокупности. На медиану влияют не столько сами значения, сколько число случаев на том или ином уровне. Следует также отметить, что медиана всегда конкретна (при большом числе наблюдений или в случае нечетного числа членов совокупности), т.к. под Ме подразумевается некоторый действительный реальный элемент совокупности, тогда как арифметическая средняя часто принимает такое значение, которое не может принимать ни одна из единиц совокупности.
Главное свойство Ме в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины: 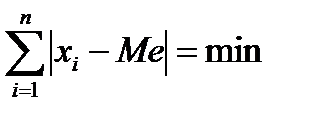 . Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.
. Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.
В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место в ранжированном вариационном ряду (каждое четвертое, пятое, десятое, двадцать пятое и т.д.). Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда.
Квартили – значения признака, делящие ранжированную совокупность на четыре равные части. Различают квартиль нижний (Q1), средний (Q2) и верхний (Q3). Нижний квартиль отделяет 1/4 часть совокупности с наименьшими значениями признака, верхний - 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3; остальные 25% превосходят Q3. Средним квартилем (Q2) является медиана.
Для расчета квартилей по интервальному ряду используют формулы:
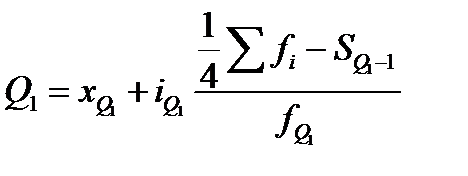 ;
;
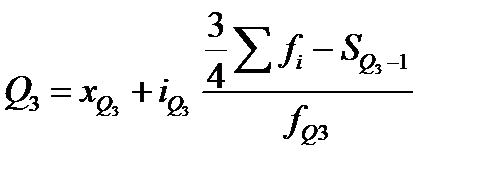 .
.
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1 – частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Децили – это значения вариант, которые делят ранжированный ряд на десять равных частей: 1-ый дециль (d1) делит совокупность в соотношении 1/10 к 9/10, 2-ой дециль (d2) - в соотношении 2/10 к 8/10 и т.д. Вычисляются децили по той же схеме, что и медиана, и квартили:
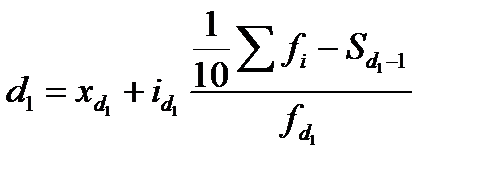 ;
;
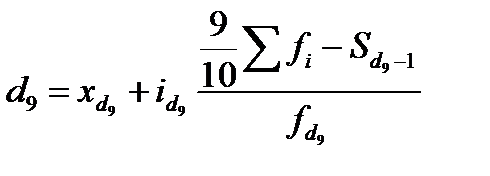 .
.
Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет глубоко и детально охарактеризовать изучаемую совокупность.
Дата добавления: 2015-12-26; просмотров: 4751;
