Пятно Пуассона или дифракция на непрозрачном диске

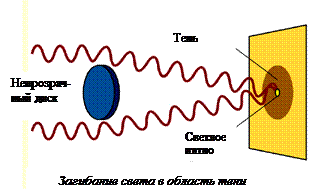
Пусть на пути плоской волны расположен непрозрачный круглый диск. Согласно представлениям геометрической оптики область на экране – это область геометрической тени. Т.к. первые m зон отсутствуют, результирующая амплитуда в точке Р равна

Е = Е_m₊₁ – Е _m₊₂+ Е _m₊₃ – Е _m₊₄ + ……± Е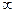= Е_m₊₁/2,

Мы видим, что если число перекрытых диском зон не слишком велико, так что убыванием Е можно пренебречь, амплитуда колебаний в центре тени от диска, практически такая же, какая была бы в точке Р при отсутствии диска. Таким образом, независимо от числа перекрываемых диском зон, векторная амплитуда в осевой точке оказывается конечной, монотонно возрастая по мере уменьшения диаметра диска.

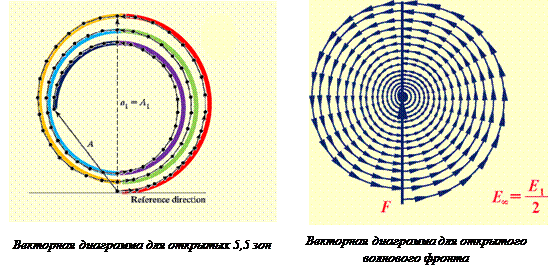
3.1.3. СПИРАЛЬ ФРЕНЕЛЯ – МЕТОД ГРАФИЧЕСКОГО СЛОЖЕНИЯ АМПЛИТУД.Рассмотрим графический метод сложения амплитуд. В этом методе мысленно разбивают волновую поверхность на узкие кольцевые подзоны, число которых велико. Амплитуда вторичных волн, изображается вектором, длина которого пропорциональна амплитуде, а фаза – углом наклона к оси абсцисс. В пределе при стремлении ширины кольцевых зон к нулю (количество их будет при этом неограниченно возрастать) векторная диаграмма принимает вид спирали, закручивающейся к ее центру (рис.).

Проследим за изменением получающихся диаграмм при постепенном увеличении диаметра отверстия в непрозрачном экране.Каждая зона на диаграмме представляет половину окружности. При переходе к следующее зоне

поворот против часовой стрелки отражает фазовый сдвиг по сравнению с волнами, пришедшими от центра отверстия на p,.
амплитуды убывают, получается не замкнутая фигура, а медленно скручивающаяся спираль.
Результат действия одной зоны – это вектор, соединяющий начало зоны с ее концом. Колебание, возбуждаемое несколькими соседними зонами, представится геометрической суммой таких векторов.

На рисунках показаны векторные диаграммы для случая, когда размер отверстия в непрозрачном экране постепенно пропускает

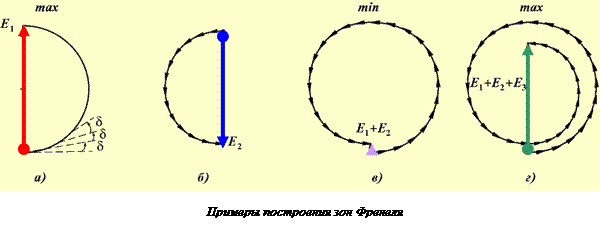· первую зону Френеля (вектор Е₁),

· вторую зону – вектор Е₂_,

· первые две зоны Е = Е₁+ Е₂» 0;

· первые три зоны Е = Е₁+ Е₂+ Е₃ » Е₁_.и т.д.

Цепочка по мере увеличения числа m закручивается в спираль и в результате действие всех зон Френеля (открытый волновой фронт) амплитуда поля в точке наблюдения вдвое меньше, чем при одной открытой первой зоне: амплитуда колебаний определяется длиной вектора Ео, проведенным из начала спирали в ее фокус.

Т. о., амплитуда колебаний в точке Р по мере увеличения радиуса отверстия меняется не монотонно: максимум сменяется минимумом и т.д. То же самое произойдет, если приближать точку наблюдения, т.е уменьшать расстояние b (рис.). Причем амплитуда (интенсивность) света максимальна в точке наблюдения на расстоянии, при котором отверстие совпадает с первой зоной Френеля.

3.1.4. ЗОННЫЕ ПЛАСТИНКИ. ИЗМЕНЕНИЕ ФАЗОВЫХ СООТНОШЕНИЙ МЕЖДУ ВТОРИЧНЫМИ ВОЛНАМИ.Из теории дифракции Френеля вытекает возможность управления формой волнового фронта и распределением интенсивности посредством изменения фазовых соотношений между вторичными волнами. Две соседние зоны действуют как источники света, колеблющиеся в противофазе — посылаемые ими световые волны в значительной степени гасят друг друга за счет деструктивной интерференции. Все четные зоны Френеля дают вклад в результирующее поле одного знака. Все нечетные – противоположного знака. Если все четные (или нечетные) зоны закрыть непрозрачной маской, то, амплитуды этих зон сонаправлены и в точке Р будет наблюдаться многократное усиление света (рис. а). По закону сохранения энергии в других точках пространства интенсивность света должна уменьшиться, то есть произойдет фокусировка света в точку Р. Такая маска называется амплитудной зонной пластинкой.На спирали Френеляостаются «работающими» только полувитки, отвечающие нечетным зонам; полувитки четных зон «выбывают из игры», поскольку заполняющие их вторичные источники оказались затененными. Амплитуда результирующего колебания Е равна при этом сумме амплитуд слагаемых колебаний, а

интенсивность для к открытых зон. Зонная пластинка Френеля обладает фокусирующими свойствами, существенно увеличивая интенсивность света в точке Р, которая является точкой фокусировки зонной пластинки.

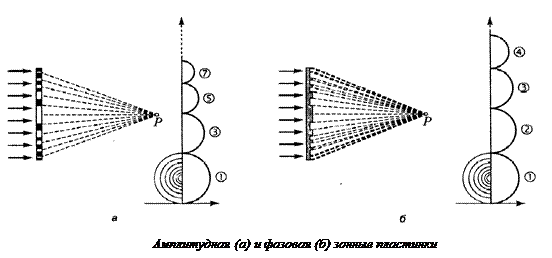Если вместо непрозрачной маски для четных (нечетных) зон ввести дополнительный фазовый сдвиг Dj = л, т. е. использовать свет всех зон, интенсивность света в фокусе возрастет еще в 4 раза. Искомого фазового сдвига можно добиться, например, путем размещения в отверстии стеклянной пластины с кольцевыми ступенями равной высоты h. Вносимая ступенькой разность хода составит

где n – показатель преломления пластины. В этом случае пластинка называется фазовой.

1. Что такое дифракция волн? Каким волновым процессам оно свойственно? 2 Как согласовать явление дифракции с прямолинейным распространением света? 1. Поясните принцип Гюйгенса-Френеля. 2. В чем состоит метод зон Френеля? 3. К чему сводится действие всей совокупности зон Френеля? 4. Какими будут освещенности в центральной точке экрана, если на отверстии укладываются одна, две, три и множество зон Френеля? 5. Будем постепенно удалять точку наблюдения от диска. Число зон Френеля, перекрываемых диском, будет постепенно уменьшаться. К чему это приводит? 6. Перечислите номера зон Френеля, которые приходят в фазе с волнами от первой зоны в области до 15 зон. 7. Имеется круглое отверстие в непрозрачной преграде, на которую падает плоская световая волна. За отверстием расположен экран. Что будет происходить с интенсивностью в центре экрана, если экран удалять от преграды? 8. Покажите с помощью векторной диаграммы, что освещенность в центре геометрической тени .

9. Волна от сферического источника S (см. рис.) интенсивнос-ти I₀ падает на непрозрачный экран А, имеющий круглое отверстие, радиуса r₀, которое открывает первую зону Френеля (см. рис.). При этом на экране В в точке Р отношение интенсивностей I_р/I₀ равно ...

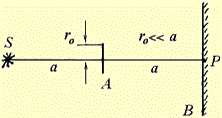
10.

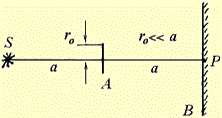Волна от сферического источника S интенсивности I₀ падает на непрозрачный круглый диск А, радиуса r₀, которое закрывает 1-ю зону Френеля (см. рис.). При этом на экране В в точке Р отношение интенсивностей I_p/I₀ близко к ...

§2. Дифракция Фраунгофера на прямоугольной щели

Ключевые понятия:

ü параметр дифракции,

ü ближняя зона,

ü дальняя зона,

ü дифракция Фраунгофера,

ü дифракционная расходимость.

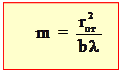3.2.1. ПАРАМЕТР ДИФРАКЦИИ. БЛИЖНЯЯ И ДАЛЬНЯЯ ЗОНЫ ДИФРАКЦИИ.В общем случае дифракционное препятствие может иметь любую форму: отверстие, диск, щель, проволока и т. д. Для анализа характера дифракции удобно использовать число зон Френеля, которое для плоских волн равно

Тогда выделяются характерные зоны:

· Дифракция не наблюдается и выполняются законы геометрической оптики, если

Наблюдается дифракция Френеля (ближняя зона), если.

В ближней зоне интенсивность света на оси пучка практически постоянна и равна интенсивности исходной световой волны. Пучок сохраняет пространственную структуру, заданную формой отверстия. В пределах отверстия помещается порядка 50зон Френеля.

Наблюдается дифракция Фраунгофера (дальняя зона), если

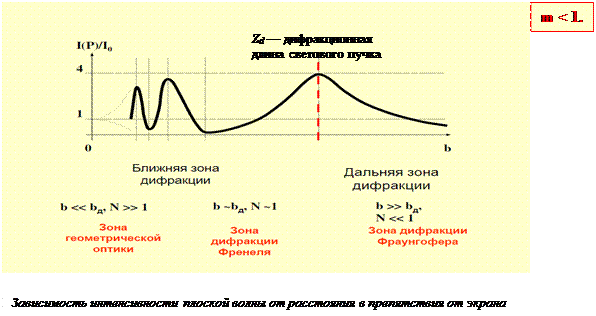В дальней зоне интенсивность света на оси пучка много меньше интенсивности исходной волны и с увеличением расстояния уменьшается обратно пропорционально квадрату рассто-яния. Световой пучок расширяется. В пределах отверстия помещается только малая центральная часть первой зоны Френеля. Характер изменения интенсивности света I на оси отверстия с ростом увеличения расстояния от экрана b при неизменном радиусе отверстия приводится на рисунке. По мере удаления от экрана периферийные зоны Френеля одна за другой начнут выходить за пределы отверстия, пока, наконец, в пределах отверстия не остается одна первая зона Френеля. В этот момент интенсивность света I в точке наблюдения достигает максимума, после чего монотонно убывает с ростом расстояния b. Расстояние Zg, при котором отверстие совпадает с первой зоной Френеля, называют дифракционной длиной светового пучка. Дифракционная длина определяет границу между ближней и дальней зонами дифракции:

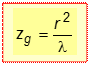
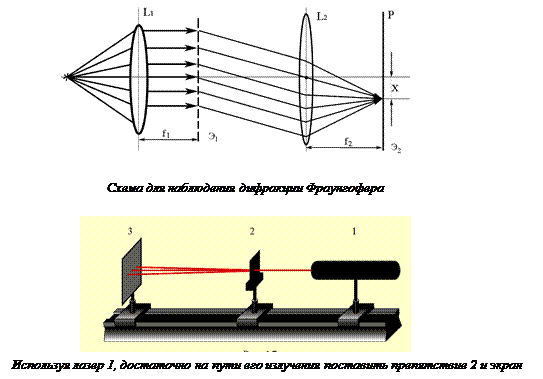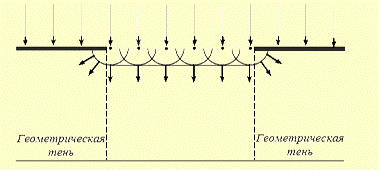
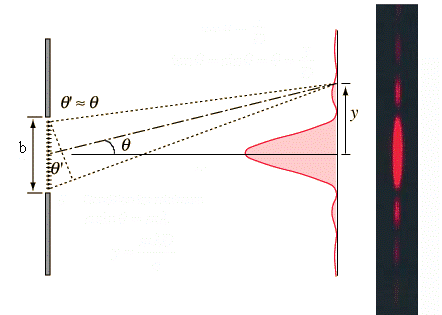
3.2.2. ДИФРАКЦИЯ ФРАУНГОФЕРА.Дифракция Фраунгофера наблюдается, если на препятствие падает плоская волна и точка наблюдения удалена на расстояние, большее дифракционной длины (m < 1). Схема для наблюдения дифракции Фраунгофера приводится на рис. Точечный источник света помещают в фокусе собирающей линзы L₁, получая плоскую волну, падающую на препятствие Э₁; за препятствием помещают вторую собирательную линзу L₂ и дифракционную картину исследуют в ее фокальной плоскости на экране Э₂.

3.2.3. ДИФРАКЦИЯ НА ПРЯМОУГОЛЬНОЙ ЩЕЛИ.Пусть плоская волна падает на прямоугольную щель шириной b. По принципу Гюйгенса пучок параллельных лучей, проходя через щель, дифрагирует под всевозможными углами в пределах от 0 до π/2.

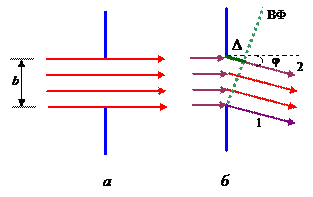Все лучи, падающие по нормали к плоскости щели (φ = 0), находятся в одной фазе (рис. а), поэтому в центре экрана возникает светлое пятно. Это соответствует главному или нулевому максимуму интенсивности. Он самый яркий.

Вторичные волны за плоскостью щели можно сгруппировать в параллельные пучки, из всей совокупности которых на рис.б представ-лены два. Для лучей, идущих под углом j от крайних элементов щели, разность хода Δ_д, равна:

Δ_д = b sin j.

Разделим ширину щели b на зоны Френеля: плоские полоски, вытянутые вдоль щели. В разности хода Δ_д уложится N зон Френеля:

N = Δ_д / (l / 2) = b sin j / (l / 2).

Если в направлении φ открыто

· четное число зон N=2m,, то амплитуда результирующей волны E_m(φ) = 0 и в этих направлениях наблюдаются минимумы интерференции:

Δ_д_min = b sin j = ml.

· нечетное число зон N = (2m + 1), то наблюдаются максимумы интерфе-ренции:

Δ_д_max = b sin j = (2m + 1) l /2.

причем, m = 1, 2, 3 и т. д. – порядок дифракции.

Интенсивности дифракционных максимумов по отношению к нулевому составляют следующий ряд чисел:

I₀: I₁: I₂: I₃ = 1 : 0.045 : 0.016 : 0.008.

Распределение интенсивности при дифракции на щели

Как видно, основная энергия световой волны при дифракции на щели сосредоточена в пределах нулевого максимума, т.е. в пределах угла sinj = ± λ/b и интенсивность достаточно сильно (как 1/m²) убывает с ростом порядка максимума. Точное выражение для распределения интенсивности света на экране:

I(j) = I₀ (sinA/A)² ,

где I₀ – интенсивность центрального максимума, параметр A = pb(sin j) /l.

3.2.4. ВЛИЯНИЕ ШИРИНЫ ЩЕЛИ НА РАСПРЕДЕЛЕНИЕ ИНТЕНСИВНОСТИ. Запишем выражение для угловой ширины главного максимума. Она равна угловому расстоянию между двумя первыми минимумами:

∆φ =(φ₊ - φ_-) = 2λ / b.

Как видно из формулы, если

· b ≤ λ – щель практически равномерно излучает по всем направлениям;

· b > λ – дифракции нет (широкая щель). В центре резкое изображение источника света, т. е. свет распространяется прямолинейно.

· b = λ, j = π/2, первый минимум отодвигается в бесконечность, а центральный максимум расплывается на весь экран.

Т.о., чем уже щель, тем сильнее дифракция.

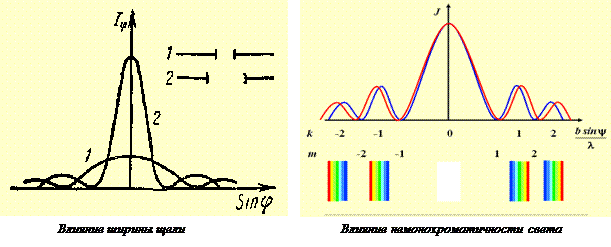
3.2.5. ВЛИЯНИЕ НЕМОНОХРОМАТИЧНОСТИ СВЕТА.Если щель освещается немонохроматичным излучением, то центральный максимум имеет радужную окраску. Остальные максимумы окрашенные в разные цвета (фиолетовым краем ближе к центру, а красным краем дальше от центра). Однако эти максимумы расплывчаты.

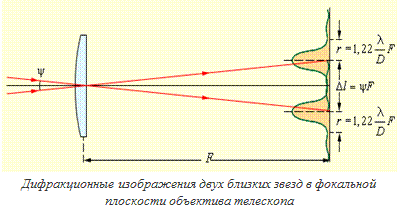
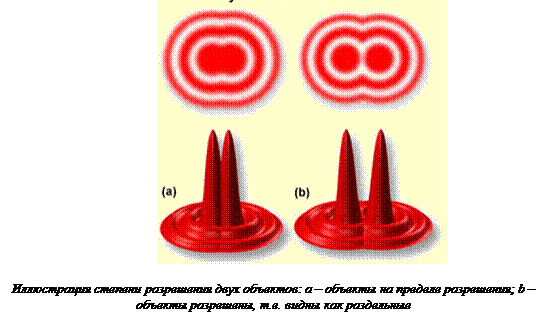
3.2.6. ДИФРАКЦИОННАЯ РАСХОДИМОСТЬ.Дифракциясвета на краях диафрагм, линз, оправ, отверстий приводит к размытию изображения точки, которое принципиально неустранимо. Рассмотрим два точечных источника света. За счет дифракции каждый из них дает кружок рассеяния в фокальной плоскости линзы c фокусным расстоянием F идиаметром D. Угловая ширина кружка рассеяния равна Δψ = 2λ / D , а линейная – r =F× ψ. Если угловое расстояние между двумя объектами больше угла дифракции φ, изображения разрешимы (ψ > φ), иначе (ψ < φ) изображения сливаются в один кружок. Объектив не разрешает изображения.

Условный критерий разрешения (критерий Рэлея) требует: два изображения находятся на пороге разрешения, когда центр дифракционного пятна одного из них совпадает с первым минимумом на дифракционной картине другого. Это соответствует минимальному угловому расстоянию между ними

Такой предел, обусловленный дифракцией, налагает на разрешающую способность линзы волновая природа света.

Глаз действует как объектив. Для диаметра зрачка 4 мм и длины волны, воспринимаемой глазом наилучшим образом λ = 0.55 мкм, угловое разрешение глаза составляет:

Ψ_min = 0,55 × 10^-3/4 » 1 × 10^-4 рад » 1 угловая минута.

1. Как меняется волновой фронт волны при дифракции? 2. Какой вид имеет картина дифракции Фраунгофера на одной щели? 3. Запишите условия максимума и минимума при дифракции на одной щели. 4. Как сказывается в случае дифракции Фраунгофера на одной щели увеличение а) ширины щели; б) длины волны? 5. Атомы имеют диаметр порядка 10^{-8 см. Можно ли, используя видимый свет, визуально наблюдать атом? Объясните, почему можно или нельзя.} 6. Оценить дифракционное уширении лазерного пучка с исходным диаметром 2 мм на расстоянии 200 м от лазера, если длина волны лазера 0.6 мкм. 7. Как будет выглядеть распределение интенсивности при сильном уменьшении размера щели? 8. В чем состоят преимущества использования в астрономических телескопах больших отражательных зеркал?

Дата добавления: 2015-12-26; просмотров: 4269;