Информационное и техническое обеспечение информационных технологий.

Информационное сообщение всегда связано с источником информации, приемником информации и каналом передачи.

Дискретные сообщения состоят из конечного множества элементов, создаваемых источником последовательно во времени. Набор элементов (символов) составляет алфавит источника.

Непрерывные сообщения задаются какой-либо физической величиной, изменяющейся во времени. Получение конечного множества сообщений за конечный промежуток времени достигается путем дискретизации (во времени), квантования (по уровню) (см. рис 1.1).

В большинстве случаев информация о протекании того или иного физического процесса вырабатывается соответствующими датчиками в виде сигналов, непрерывно изменяющихся во времени. Переход от аналогового представления сигнала к цифровому дает в ряде случаев значительные пре­имущества при передаче, хранении и обработке информации. Преобразование осуществляется с помощью специальных устройств – преобразовате­лей непрерывных сигналов и может быть выполнено дискретизацией во времени и квантованием по уровню.

Рассмотрим разновидности сигналов, которые описываются функ­цией x(t).

1. Непрерывная функция непрерывного аргумента. Значения, которые могут принимать функция x(t) и аргумент t, заполняют промежутки (x_min, x_max) и (-T, T) соответственно.

2. Непрерывная функция дискретного аргумента. Значения функции x(t) определяются лишь на дискретном множестве значений аргумента t_i, i=0±1±2, … Величина x(t_i) может принимать любое значение в интервале (x_min, x_max).

3. Дискретная функция непрерывного аргумента. Значения, которые может принимать функция x(t), образуют дискретный ряд чисел х₁, х₂,..., x_k. Значение аргумента t может быть любым в интервале (-Т, Т).

4. Дискретная функция дискретного аргумента. Значения, которые могут принимать функция х(t) и аргумент t, образуют дискретные ряды чисел x₁, x₂, ..., x_k и t₁, t₂, ..., t_k, заполняющие интервалы (x_min, x_max) и (-Т,Т) соответственно.

Первая из рассмотренных разновидностей принадлежит непрерывным сигналам, вторая и третья — дискретно-непрерывным, а четвертая — дискретным сигналам.

Операцию, переводящую информацию непрерывного вида в информа­цию дискретного вида, называют квантованием по времени, или дискретизацией. Следовательно, дискретизация состоит в преобразовании сигнала x(t) непрерывного аргумента t в сигнал x(t_i) дискретного аргумента t_i.

Квантование по уровню состоит в преобразовании непрерывного множества значений сигнала x(t_i) в дискретное множество значений x_k, k = =0,1,..., (m - 1); x_k Î (x_min, x_max) (третий вид сигнала).

Совместное применение операций дискретизации и квантования по уровню позволяет преобразовать непрерывный сигнал x(t) в дискретный по координатам х и t (четвертая разновидность).

В результате дискретизации исходная функция x(t) заменяется совокупностью отдельных значений x(t₁). По значениям функции x(t_i) можно восстановить исходную функцию x(t) с некоторой погрешностью. Функ­цию, полученную в результате восстановления (интерполяции) по значени­ям x(t_i), будем называть воспроизводящей и обозначать V(t).

При дискретизации сигналов приходится решать вопрос о том, как часто следует проводить отсчеты функции, т. е. каков должен быть шаг дискретизации Dt_i = t_i – t_i-1. При малых шагах дискретизации количество отсчетов функции на отрезке обработки будет большим и точность воспроиз­ведения — высокой. При больших шагах дискретизации количество отсче­тов уменьшается, но при этом, как правило, снижается точность восстанов­ления. Оптимальной является такая дискретизация, которая обеспечивает представление исходного сигнала с заданной точностью при минимальном количестве отсчетов.

Методы дискретизации и восстановления информации классифицируются в зависимости от регулярности отсчета, критерия оценки точности дискретизации и восстановления, вида базисной функции, принципа при­ближения.

Регулярность отсчета определяется равномерностью дискретизации.

Дискретизация называется равномерной (рис. 1.3, а), если длительность интервалов Dt_i = const на всем отрезке обработки сигнала. Методы равномерной дискретизации широко применяют, так как алгоритмы и аппаратура для их реализации достаточно просты. Однако при этом возможна значи­тельная избыточность отсчетов.

Дискретизация называется неравномерной (рис. 1.3,6), если длитель­ность интервалов между отсчетами Dt_i , различна, т. е. Dt_i = var . Выделяют две группы неравномерных методов: адаптивные и программируемые. При адаптивных методах интервалы Dt_i , изменяются в зависимости от текущего изменения параметров сигналов. При программируемых методах интерва­лы Dt_i , изменяются либо оператором на основе анализа поступающей информации, либо в соответствии с заранее установленной программой работы.

Рис. 1.3. Способы дискретизации информации

Критерии оценки точности дискретизации сигнала выбираются получателем информации и зависят от целевого использования сигнала и возможностей аппаратной (программной) реализации. Чаще других использу­ются критерий наибольшего отклонения, среднеквадратический, интегральный и вероятностный.

Тип базисных (приближающих, воспроизводящих) функций в основном определяется требованиями ограничения сложности устройств (программ) дискретизации и восстановления сигналов.

Воспроизводящие функции v(t) обычно совпадают с приближающими функциями p(t), хотя в общем случае они могут отличаться друг от друга. Чаще всего для дискретизации и восстановления используют ряды Фурье и Котельникова, полиномы Чебышева и Лежандра, степенные полиномы, функции Уолша и Хаара, гипергеометрические функции.

При равномерной дискретизации шаг Dt и частота отсчетов F₀ — постоянные величины (рис. 1.3, а). Модель равномерной дискретизации очень хорошо подходит к модели синхронных автоматов. Теорема Котельникова позволяет осуществлять выбор шага дискретизации, что существенным об­разом может повлиять на количество и скорость поступления информации для обработки.

Рис. 1.4. Квантование по уровню

Квантование по уровню состоит в преобразовании непрерывных зна­чений сигнала x(t_i) в моменты отсчета t_i, в дискретные значения (рис. 1.4). В соответствии с графиком изменения функции x(t) ее истинные значения представляются в виде заранее заданных дискретных уровней 1, 2, 3, 4, 5 или 6. Функция в моменты отсчета может задаваться или точно (значе­ние х₂ – уровень 4), или с некоторой погрешностью (значение х₁ — уровень 2, значение x₃ — уровень 6).

Квантование по уровню может быть рав­номерным и неравномерным в зависимости от величины шага квантования. Под шагом (ин­тервалом) квантования d_m понимается раз­ность d_m = x_m – x_m-1, где x_m, x_m-1 – соседние уровни квантования.

Уровень квантования для заданного значе­ния сигнала x(t) можно выразить двумя способами:

1) сигнал x(t_i) отождествляется с ближайшим уровнем квантования;

2) сигнал x(t_i) отождествляется с ближайшим меньшим (или боль­шим) уровнем квантования.

Так как в процессе преобразования значение сигнала x(t) отображает­ся уровнем квантования x_m , а каждому уровню m может быть поставлен в соответствие свой номер (число), то при передаче или хранении информации можно вместо истинного значения величины x_m­ использовать соответствующее число m. Истинное значение уровня квантования легко восстано­вить, зная масштаб по шкале х. Для представления m уровней квантования с помощью неизбыточного равномерного кода потребуется n=log₂m раз­рядов. Такое преобразование сопровождается шумами или погрешностью квантования. Погрешность квантования связана с заменой истинного зна­чения сигнала x(t_i) значением, соответствующим уровню квантования x_m . Максимальная погрешность квантования зависит от способа отождествле­ния сигнала с уровнем квантования. Для первого из рассмотренных спосо­бов она равна 0,5d_m, для второго – d_m.

Чем меньше шаг квантования, тем меньше погрешность квантования. Можно принять, что погрешность квантования в пределах шага квантова­ния имеет равновероятный закон распределения, т. е. любое значение функции в пределах шага будет равновероятным.

Наиболее часто используются степенные алгебраические полиномы вида V(t)= 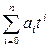, где n — степень полинома, а_i — действительные коэффициенты. Из этого класса функций наиболее полно исследовано примене­ние полиномов нулевой и первой степени. Алгебраические полиномы удобны для программирования и обработки на ЭВМ.

Выбор оптимальной системы функции представляет определенные трудности, так как при решении задачи минимизации числа дискретных характеристик для описания сигнала с заданной точностью должны учитывать сложность аппаратуры (программ), допустимое время задержки в вы­даче информации и другие факторы.

Метод дискретизации при преобразовании непрерывной информации в дискретную влияет на количество информации, которую надо хранить или преобразовывать в ЭВМ. Важна теорема Котельникова, согласно которой функция, имеющая ограниченный спектр частот, полностью определяется дискретным множеством своих значений, взятых с частотой отсчетов:

F₀ = 2f_m , (1.9)

где f_m = 2pw_m – максимальная частота в спектре частот S(jw) сигнала x(t); w_m –угловая скорость.

Функция x(t) воспроизводится без погрешностей по точным значе­ниям x(t_i) в виде ряда Котельникова:

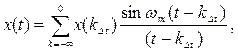(1.10)

где Dt – шаг дискредитации.

Теорема Котельникова справедлива для сигналов с ограниченным спектром. Реальные сигналы — носители информации — имеют конечную длительность. Спектр таких сигналов не ограничен, т. е. реальные сигналы не соответствуют в точности модели сигнала с ограниченным спектром, и применение теоремы Котельникова к реальным сигналам связано с погрешностями при восстановлении сигналов по формуле (1.10) и неопределенностью выбора шага дискретизации или частоты отсчетов.

Для практических задач, однако, идеально точное восстановление функций не требуется, необходимо лишь восстановление с заданной точностью. Поэтому теорему Котельникова можно рассматривать как прибли­женную для функций с неограниченным спектром. На практике частоту отсчетов часто определяют по формуле

F₀ = 2f_maxk₃ , (1.11)

где k₃ —коэффициент запаса (обычно 1,5 < k₃ < 6 ); f_max —максималь­ная допустимая частота в спектре сигнала x(t), например, с учетом доли полной энергии, сосредоточенной в ограниченном частотой спектре сиг­нала.

Из вышеизложенного следует, что преобразование непрерывной информации в дискретную может сопровождаться сжатием информации (уменьшением ее количества). Квантование по уровню — один из способов сжатия информации.

Квантование и дискретизация находят широкое применение в преобразователях информации, используемых при связи ЭВМ с конкретными объектами (процессами).