Условия пластичности стержней
Прежде чем начать говорить об условиях пластичности оболочек, следует напомнить об условиях пластичности стержней.
Напряжённое состояние колонн нижних этажей каркасов многоэтажных зданий, арок различного назначения и других конструкций характеризуется наличием изгибающих моментов М и продольных сил N в сечении стержня. Для сравнения здесь рассматриваются два типичных примера условий текучести стержней.
Известно, что по мере увеличения внешней нагрузки в стержне возникает сначала текучесть на одной кромке (рис. 13.7). Затем зона, в которой напряжения достигли предела текучести 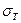 , будет распространяться в глубь сечения; напряжения на противоположной кромке при этом стремятся к пределу текучести другого знака и, наконец, достигают его. После этого в сечении возникают две зоны текучести, которые при увеличении M и N распространяются навстречу друг другу.
, будет распространяться в глубь сечения; напряжения на противоположной кромке при этом стремятся к пределу текучести другого знака и, наконец, достигают его. После этого в сечении возникают две зоны текучести, которые при увеличении M и N распространяются навстречу друг другу.
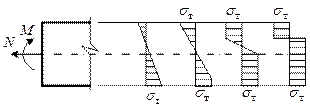
Рис. 13.7
В конце концов наступит предельное состояние сечения с очень малым упругим ядром, отвечающее большим краевым деформациям. В целях упрощения расчетов за предельную эпюру принимают эпюру, состоящую из двух прямоугольников неодинаковой высоты. Это напряженно – деформированное состояние сечения стержня соответствует образованию в сечении «шарнира» текучести.
Для стержня прямоугольного сечения предельные значения усилий M и N и их сочетание, приводящее к образованию шарнира текучести, нетрудно найти. С этой целью в растянутой (нижней) зоне сечения необходимо отделить участок эпюры, равный по площади эпюре напряжений сжатой зоны (рис. 13.7, 13.8). Тогда продольная сила N, возникающая в сечении, должна уравновеситься остальной (заштрихованной на рисунке) частью эпюры растягивающих или сжимающих напряжений
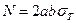 , (13.3)
, (13.3)
где 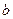 - ширина сечения.
- ширина сечения.

Рис. 13.8
Изгибающий момент равен объему эпюры сжимающих напряжений, умноженному на плечо 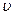 =
= 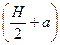 пары внутренних сил. Равнодействующая эпюры этих напряжений равна
пары внутренних сил. Равнодействующая эпюры этих напряжений равна 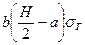 . В таком случае момент M, возникающий в сечении, находится по формуле
. В таком случае момент M, возникающий в сечении, находится по формуле
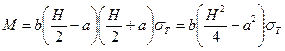 .
.
Подставив величину продольной силы N, определяемую по формуле (13.3), в последнее выражение, находят соотношение между продольной силой и изгибающим моментом в предельном состоянии поперечного сечения стержня
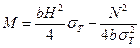 . (13.4,а)
. (13.4,а)
Обозначив предельные значения изгибающих моментов и продольных сил 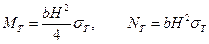 ,
,
полученное соотношение можно переписать в виде*
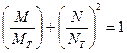 . (13.4,б)
. (13.4,б)
Если к тому же ввести обозначения для безразмерных величин продольных сил 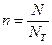 и изгибающих моментов
и изгибающих моментов 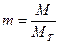 , то условие пластичности сечения запишется более компактно
, то условие пластичности сечения запишется более компактно
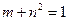 . (13.4,в)
. (13.4,в)
Условие предельного состояния сечения графически изображается в виде двух парабол а, симметричных относительно оси 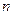 (рис. 13.9). Нижняя парабола служит условием текучести сечения на участках стержня с отрицательными моментами. Поэтому в общем случае условие текучести можно представить в виде
(рис. 13.9). Нижняя парабола служит условием текучести сечения на участках стержня с отрицательными моментами. Поэтому в общем случае условие текучести можно представить в виде 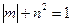 , где
, где 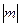 обозначает модуль изгибающего момента.
обозначает модуль изгибающего момента.
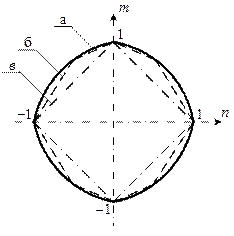
а б в


Рис. 13.9
Для стержней, поперечное сечение которых отличается от прямоугольного, условия текучести будут отличаться от (13.4). Например, для сечений, близких к двутавровым (у которых стенка сильно ослаблена), т. н. идеальных двутавров (рис. 13.9,в), условие текучести принимает вид
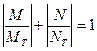 , (13.5,а)
, (13.5,а)
или
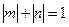 . (13.5,б)
. (13.5,б)
Графически оно может быть проиллюстрировано квадратом «в», вписанным в параболу (рис. 13.9). Для других сечений, таких, как круглые, двутавры из сортаментов и др., условия текучести будут представлены в виде многоугольников, расположенных между параболой и квадратом. В частности, условие текучести трехслойного прямоугольного сечения аппроксимируется восьмиугольником «б». Перечисленные условия пластичности часто используются в расчётах несущей способности сжато – изогнутых стоек и арок [8].
Доказано, что для криволинейных стержней, радиус кривизны которых в 8-10 раз превышает высоту сечения, распределение напряжений в упруго- пластической стадии и в состоянии полной пластичности сечения стержня практически не отличается от того, которое имеет место в сечении прямого бруса при тех же внутренних силовых факторах, и, следовательно, при анализе предельного равновесия сжато-изогнутых стержней или арок, как стержней малой кривизны, возможно применение условия предельного состояния сечения, полученного для прямолинейного стержня.
Если при исследовании несущей способности учитывать ещё и поперечные силы Q в сжато-изогнутых стержней, то условия текучести усложняются. Например, для стержня двутаврового сечения с тонкой стенкой (идеального двутавра) условие текучести графически изображается в виде поверхности шара, симметрично срезанной плоскостями с четырех сторон (рис. 13.10).
 |
Рис. 13.10
На рисунке показана только четверть этой поверхности, уравнение которой имеет вид
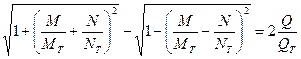 , (13.6,а)
, (13.6,а)
где QТ – предельное значение усилия Q в сечении. В безразмерных параметрах условие (13.6,а) записывается короче, а именно:
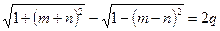 . (13.6,б)
. (13.6,б)
Здесь m, n обозначают параметры величин внутренних усилий M и N, а 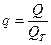 - характеризует безразмерный параметр поперечной силы в сечении стержня.
- характеризует безразмерный параметр поперечной силы в сечении стержня.
В работах [9], [10] автора на основе приведенных условий пластичности выполнен подробный анализ пластического состояния арок кругового очертания. При этом было исправлено бытовавшее прежде ошибочное представление о характере разрушения пологих арок.
13.3. Ассоциированный закон течения и его геометрическое представление
В теории пластичности известны различные модели пластического деформирования твёрдых тел. Наибольшее распространение получили теория пластического потенциала или пластического течения и деформационная теория [8]. Автор придерживается первой из них, и потому дальнейшее изложение раздела основано на теории пластического потенциала.
В основу теории пластического течения положен ассоциированный закон течения, который устанавливает связь между приращениями скоростей деформаций 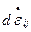 и напряжениями
и напряжениями 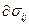 при пластическом деформировании в виде
при пластическом деформировании в виде
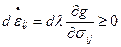 . (13.7,а)
. (13.7,а)
В этом выражении 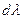 является неопределённым множителем, а функция
является неопределённым множителем, а функция 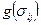 представляет собой в общем случае функцию нагружения* или пластический потенциал. Таковым, например, в случае пластичности сечения идеального двутавра служит условие текучести вида (13.5). Очевидно, точкам поверхности нагружения или кривой пластичности в случае плоского напряжённого состояния соответствует пластическое течение, а упругому состоянию – точки, лежащие внутри поверхности или кривой.
представляет собой в общем случае функцию нагружения* или пластический потенциал. Таковым, например, в случае пластичности сечения идеального двутавра служит условие текучести вида (13.5). Очевидно, точкам поверхности нагружения или кривой пластичности в случае плоского напряжённого состояния соответствует пластическое течение, а упругому состоянию – точки, лежащие внутри поверхности или кривой.
Закону течения можно дать простое геометрическое истолкование. Если условие текучести g(Fij) представить в виде некоторой поверхности в (шести мерном) пространстве компонент тензора напряжений 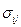 , а тензору напряжений сопоставить вектор Fij, то тогда согласно определению (13.7,а) вектор пластических деформаций gij следует направить по нормали к данной поверхности (рис. 13.11). При этом напряжённое состояние некоторой частицы тела, соответствующее пластическому, изображается в виде вектора, касающегося границы поверхности
, а тензору напряжений сопоставить вектор Fij, то тогда согласно определению (13.7,а) вектор пластических деформаций gij следует направить по нормали к данной поверхности (рис. 13.11). При этом напряжённое состояние некоторой частицы тела, соответствующее пластическому, изображается в виде вектора, касающегося границы поверхности 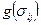 . Изображающим точкам, лежащим внутри поверхности, соответствуют векторы упругих напряжений F
. Изображающим точкам, лежащим внутри поверхности, соответствуют векторы упругих напряжений F 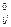 .
.
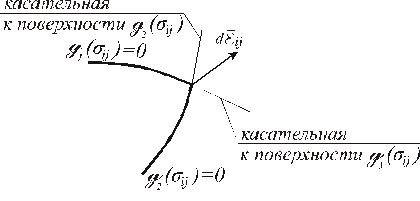
Рис. 13.11
Ассоциированный закон течения (13.7,а) является следствием принципа максимума работы пластической деформации, поскольку условием относительного максимума приращения пластической работы 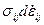 по методу Лагранжа служит уравнение
по методу Лагранжа служит уравнение
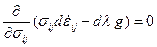 ; (13.8)
; (13.8)
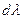 называют чаще множителем Лагранжа.
называют чаще множителем Лагранжа.
Принцип максимума работы пластической деформации, представленный в форме скалярного неравенства
( 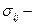
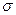
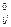 )
) 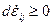 , (13.9)
, (13.9)
указывает на то, что угол между векторами приращения напряжений (Fij -F 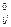 ) и деформаций gij в процессе пластического деформирования должен сохраняться острым (см. рис. 13.11). Отсюда вытекает свойство выпуклости поверхности нагружения или текучести.
) и деформаций gij в процессе пластического деформирования должен сохраняться острым (см. рис. 13.11). Отсюда вытекает свойство выпуклости поверхности нагружения или текучести.
При наличии угловых точек или рёбер у поверхности текучести вектор пластических деформаций заключён в пределах пространственного угла, образованного нормалями гладких участков поверхности, примыкающих к углу или ребру. Математическим выражением указанного случая будет более общая форма ассоциированного закона течения в виде
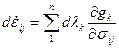 , (13.10)
, (13.10)
где n – число гладких участков поверхности вблизи угла.
13.5. Теоремы теории предельного равновесия
Теория предельного равновесия (для краткости именуемая ТПР) феноменологически** основывается на том подтвержденном обширными экспериментальными исследованиями и натурными наблюдениями факте, что для многих видов конструкций, изготовленных из материалов, обладающих достаточно выраженными пластическими свойствами, исчерпание несущей способности проявляется как развитие значительных деформаций и перемещений при практически неизменной нагрузке. График равновесных состояний (называемый также графиком деформирования) при постепенно возрастающем параметре нагрузки р для таких конструкций показан на рис. I3.1, где 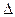 - характерное перемещение.
- характерное перемещение.
Основной задачей ТПР является определение предельного значения параметра нагрузки рТ (по иной терминологии рТ – предельная, или разрушающая, нагрузка, несущая способность) без исследования процесса деформирования. Предельное состояние можно рассматривать как состояние, предшествующее разрушению. Поэтому предельное состояние иногда называют состоянием пластического разрушения или потерей несущей способности сооружения.
В результате решения задачи ТПР выявляется схема разрушения, но при этом значения деформаций и перемещений остаются неопределенными. При р=рТ в результате развития зон пластичности в наиболее напряжённых сечениях конструкция утрачивает геометрическую неизменяемость и превращается в своеобразный механизм - механическую систему, обладающую кинематической подвижностью.
С формальной точки зрения ТПР является прикладной областью теории идеальной пластичности, основанной на использовании простейшей аппроксимации свойств реальных пластически деформируемых материалов - модели жесткопластического тела, характеризуемого диаграммой, приведенной на рис. 13.2,a.
Основные теоремы теории предельного равновесия впервые сформулированы А.А. Гвоздевым в 1936 году. Для их оказательства вводятся понятия статически возможных полей напряжений и кинематически допустимых полей скоростей перемещений.
Определение 1.
Статически возможным называется распределение (поле) напряжений или внутренних усилий 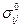 , удовлетворяющее:
, удовлетворяющее:
а) уравнениям равновесия
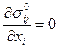 ,
,
б) статическим граничным условиям
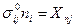
(здесь индексы отличаются от обозначений, принятых в работе [8]) при заданных воздействиях 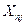 на поверхности деформируемого твёрдого тела
на поверхности деформируемого твёрдого тела
в) и условию 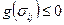 .
.
Замечание. Принцип максимума работы пластической деформации с использованием определения 1 формулируется следующим образом: приращение работы пластической деформации 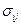
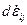 имеет максимальное значение для действительного напряжённого состояния по сравнению с любым статически возможным.
имеет максимальное значение для действительного напряжённого состояния по сравнению с любым статически возможным.
Статическая теорема ТПР:
Нагрузка, соответствующая статически возможному состоянию, меньше, чем предельная.
В соответствии с принципом возможных перемещений для действительного напряжённого состояния произвольного объёма тела (рис. 13.12) можно записать
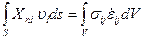 .
.

Рис. 13.12
Аналогично, для любого статически возможного состояния того же объёма справедливо равенство
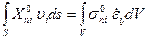 .
.
Вычитая из первого равенства второе
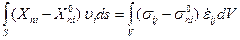
и принимая во внимание неравенство (13.11), легко установить, что
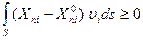
или
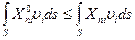 ,
,
т.е. мощность нагрузки, отвечающей статически возможному состоянию, на действительных скоростях перемещений меньше мощности действительной нагрузки на тех же скоростях.
Если нагрузки являются сосредоточенными силами 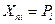 , то согласно полученному неравенству
, то согласно полученному неравенству
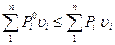 .
.
При действии единственной нагрузки Р должно соблюдаться неравенство
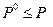 .
.
При определении предельной величины нагрузки необходимо рассмотреть различные статически возможные состояния тела или сооружения в целом и вычислить нагрузки, вызывающие эти состояния. Наибольшее значение одной из них будет ближе всего соответствовать предельному состоянию или исчерпанию несущей способности сооружения. В общем случае достаточно рассмотреть какое-либо одно статически возможное состояние сооружения и максимизировать значение нагрузки, отвечающей этому состоянию, например, с помощью методов линейного программирования [8].
Метод определения предельной нагрузки путём рассмотрения статически возможных состояний сооружений называется статическим. С его помощью определяется нижняя граница значения предельной нагрузки.
Определение 2.
Кинематически допустимым называется распределение (поле) скоростей перемещений 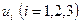 или деформаций, удовлетворяющее:
или деформаций, удовлетворяющее:
1) условиям непрерывности
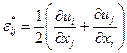 ,
,
2) заданным условиям совместности деформаций и кинематическим граничным условиям на поверхности тела.
Кинематическая теорема ТПР:
Нагрузка, соответствующая кинематически допустимому полю скоростей, больше, чем предельная.
Рассматривая работу напряжений действительного состояния произвольного объёма тела на кинематически допустимых перемещениях (рис. 13.13) в соответствии с принципом возможных перемещений, можно утверждать, что
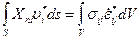 .
.

Рис 13.13
Правую часть данного равенства легко преобразовать, воспользовавшись определением кинематически возможного напряжённого состояния тела
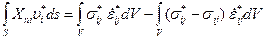 .
.
Здесь 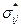 - напряжения, соответствующие кинематически допустимым перемещениям, которые могут и не удовлетворять условиям равновесия тела.
- напряжения, соответствующие кинематически допустимым перемещениям, которые могут и не удовлетворять условиям равновесия тела.
Так как в соответствии с принципом максимума работы пластической деформации справедливо неравенство (13.11), то
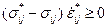 .
.
С учётом данного обстоятельства преобразованное равенство принимает форму неравенства вида
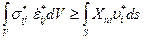 ,
,
где 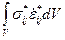 представляет собой мощность внутренних напряжений в кинематически допустимом состоянии тела.
представляет собой мощность внутренних напряжений в кинематически допустимом состоянии тела.
Конечно, всегда можно подобрать нагрузку таким образом, что её мощность на кинематически допустимом поле перемещений будет равна мощности соответствующих напряжений, т.е.
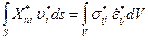
Тогда с учётом предыдущего неравенства будет сохраняться неравенство следующего вида:
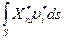
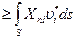 ,
,
в соответствии с которым мощность нагрузки, отвечающей кинематически допустимомому состоянию тела на кинематически допустимом поле скоростей перемещений, всегда больше мощности действительной нагрузки на тех же скоростях.
При действии только сосредоточенных сил, очевидно,
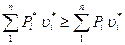 .
.
При действии единственной силы Р должно соблюдаться неравенство
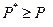 .
.
Метод вычисления предельной нагрузки с помощью полученной формулы называется кинематическим.
Как и в случае применения статического метода, и здесь на основе какой–либо одной вероятной схемы механизма разрушения, т.е. кинематически допустимого поля скоростей перемещений сооружения, путём минимизации значения нагрузки, отвечающей этому полю, например, методом линейного программирования можно найти точную её величину [2, 13].
Если при определении несущей способности сооружения использовать оба метода, то можно дать двустороннюю оценку величины предельной нагрузки
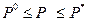 .
.
В следующих подразделах лекции подробно излагается методика определения предельной нагрузки для сферических оболочек на основе теорем теории предельного равновесия.
13.5. Уравнения состояния сферических оболочек
Напряженно-деформированное состояние упругих тонких оболочек в общем случае характеризуется совокупностью трёх групп уравнений, в целом составляющих 17 уравнений, среди которых:
I. пять уравнений равновесия:
· 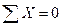 ,
, 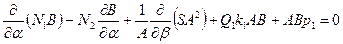 ,
,
· 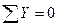 ,
, 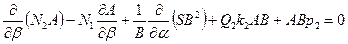 ,
,
· 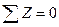 ,
, 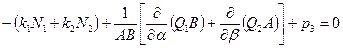 ,
,
· 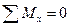 ,
, 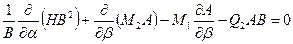 ,
,
· 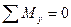 ,
, 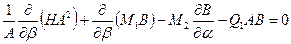 ,
,
II. шесть геометрических зависимостей между перемещениями и деформациями:
-
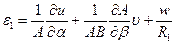 ,
, -
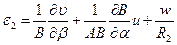 ,
, -
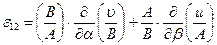 ,
, -
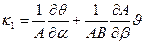 ,
, -
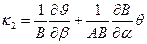 ,
, -
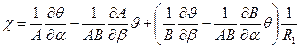
III. и ещё шесть уравнений, образующих группу физических уравнений (см. формулы (6.10) в разделе 6):
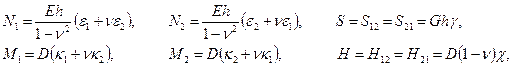
связывающих внутренние усилия и деформации.
Очевидно, при решении задач пластичности оболочек последняя группа уравнений не используется вовсе. В силу вступают соотношения теории пластичности.
Исследование несущей способности сферической оболочки*, нагруженной равномерным давлением, осуществляется на основе условий равновесия сферических оболочек (рис. 13.14):
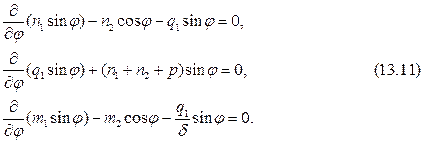
Указанные уравнения получены на основе уравнений I группы уравнений состояния, в которых принято 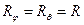 . Здесь введены следующие обозначения:
. Здесь введены следующие обозначения: 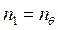 ,
, 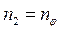 - безразмерные меридиональное и окружное усилия, т.е. усилия
- безразмерные меридиональное и окружное усилия, т.е. усилия 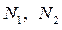 , отнесенные к предельному значению
, отнесенные к предельному значению 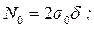
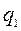 - отнесенное к
- отнесенное к 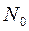 перерезывающее усилие в меридиальном направлении
перерезывающее усилие в меридиальном направлении 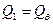 ;
; 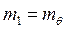 ,
, 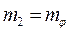 - меридиональный и окружной изгибающие моменты, отнесенные к предельному значению момента
- меридиональный и окружной изгибающие моменты, отнесенные к предельному значению момента 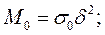
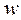 и
и 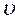 – нормальные и меридиональный компоненты смещения срединной поверхности оболочки, отнесенные к радиусу оболочки R;
– нормальные и меридиональный компоненты смещения срединной поверхности оболочки, отнесенные к радиусу оболочки R; 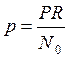 - параметр внешнего давления (рис. 13.14).
- параметр внешнего давления (рис. 13.14).
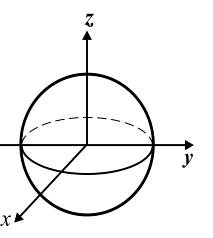
Рис. 13.14
Кроме того, справедливы также зависимости между деформациями и перемещениями срединной поверхности, которые для сферической оболочки принимают вид [1]:
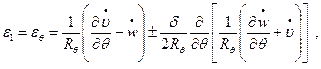 (13.12,а)
(13.12,а)
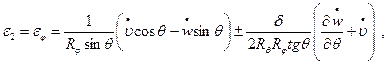 (13.12,б)
(13.12,б)
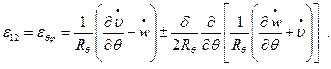 (13.12,в)
(13.12,в)
Очевидно, как при определении предельных нагрузок оболочек, так и при изложении в дальнейшем динамики оболочек с учётом пластических свойств место физических соотношений (6.10) будут занимать условия пластичности оболочек и ассоциированный закон течения.
13.6 Условия пластичности оболочек. Гиперповерхности текучести
Условия пластичности оболочек 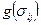 , т. н. конечные соотношения между обобщёнными усилиями, при которых возникает пластичность в оболочках, впервые получены советским учёным Ильюшиным А. А. на основе условия текучести Мизеса – Губера для плоского напряжённого состояния в 1946 г. [8]. В пятидесятых годах прошлого века за рубежом проблемой формирования условий пластичности активно занимались Онат Е., Прагер В. , Ходж Ф. Г. (США) и др. Воспользовавшись условием текучести Треска Сен – Венана и применив теорию пластического течения, вначале они вывели ряд соотношений между обобщёнными характеристиками напряжённого состояния цилиндрической оболочки, при которых возникает текучесть материала в наиболее напряжённых зонах оболочки. Геометрически указанные зависимости моут быть представлены т. н. поверхностями текучести. При этом вследствие нелинейности условий текучести поверхности имеют сложное очертание. Из – за этого возникают трудности при формулировке ассоциированного закона течения. В дальнейшем Друккер Д. К. [3], Ерхов М. И. [5], Ходж Ф. Г. предложили аппроксимировать поверхности текучести гиперплоскостями, что равносильно линеаризации нелинейных условий. При этом была дана оценка степени приближённости гиперповерхностей (см. п. 13.6).
, т. н. конечные соотношения между обобщёнными усилиями, при которых возникает пластичность в оболочках, впервые получены советским учёным Ильюшиным А. А. на основе условия текучести Мизеса – Губера для плоского напряжённого состояния в 1946 г. [8]. В пятидесятых годах прошлого века за рубежом проблемой формирования условий пластичности активно занимались Онат Е., Прагер В. , Ходж Ф. Г. (США) и др. Воспользовавшись условием текучести Треска Сен – Венана и применив теорию пластического течения, вначале они вывели ряд соотношений между обобщёнными характеристиками напряжённого состояния цилиндрической оболочки, при которых возникает текучесть материала в наиболее напряжённых зонах оболочки. Геометрически указанные зависимости моут быть представлены т. н. поверхностями текучести. При этом вследствие нелинейности условий текучести поверхности имеют сложное очертание. Из – за этого возникают трудности при формулировке ассоциированного закона течения. В дальнейшем Друккер Д. К. [3], Ерхов М. И. [5], Ходж Ф. Г. предложили аппроксимировать поверхности текучести гиперплоскостями, что равносильно линеаризации нелинейных условий. При этом была дана оценка степени приближённости гиперповерхностей (см. п. 13.6).
Линеаризация условий текучести осуществляется путём перехода к расчёту двухслойных оболочек. Слои оболочек обладают бесконечно малой толщиной и располагаются на равном удалении от срединной поверхности Такое сечение принято называть идеальным. Для каждого слоя значения интенсивности скорости деформаций принимают равными:
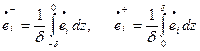 , (13.13)
, (13.13)
где
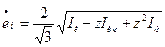 (13.14)
(13.14)
- интенсивность скорости деформаций плиты оболочки, а
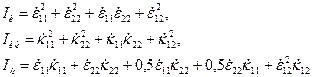
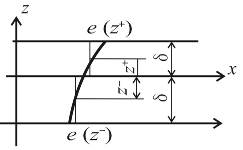
- квадратичные формы деформаций [5]. Следовательно, действительное нелинейное (по гиперболе) распределение интенсивности скорости деформаций 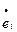 по толщине оболочки согласно (13.13) заменяется на кусочно - линейное, постоянное в пределах толщины каждой половины сечения (рис. 13.15,а, б).
по толщине оболочки согласно (13.13) заменяется на кусочно - линейное, постоянное в пределах толщины каждой половины сечения (рис. 13.15,а, б).
а
б
Рис. 13.15
Вследствие этого компоненты девиатора напряжений в тех же пределах будут постоянными:
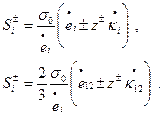
Т. к. компоненты девиатора напряжений можно выразить непосредственно через напряжения:
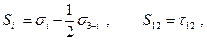
то в результате несложных преобразований напряжения в каждом слое оказывается возможным представить как функции параметров обобщённых усилий оболочки:
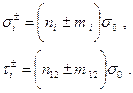
Здесь
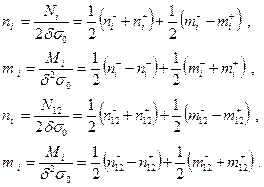 (13.15)
(13.15)
Величины внутренних сил 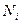 и моментов
и моментов 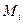 , по определению, равны:
, по определению, равны:
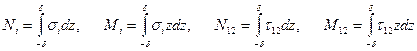 .
.
Для вывода условий текучести оболочек следует воспользоваться любым из известных в теории пластичности условием текучести, справедливым для плоского напряжённого состояния. В частности, условие пластичности Треска – Сен–Венана, графически изображаемое в форме шестиугольника в плоскости главных напряжений (рис. 13.12), с помощью определений усилий по (13.15) принимают вид:
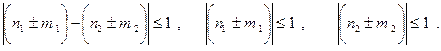 (13.16)
(13.16)
Полученные неравенства в абстрактном пространстве четырёх измерений графически являют собой совокупность плоскостей, ограничивающих область пространства, внутренние точки которой характеризуют упругое состояние оболочки. Указанные плоскости в рассматриваемом пространстве образуют гиперповерхность текучести оболочки (рис. 13.16).
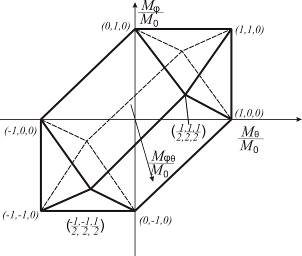
Рис. 13.16
В том случае, когда напряжения в оболочке в каком - либо месте достигают предела текучести, одно из указанных неравенств переходит в равенство. Его часто называют уравнением текучести. В совокупности с ассоциированным законом течения уравнение текучести является важнейшей характеристикой пластической фазы деформирования оболочек.
13.7 Статический метод определения предельного давления
на сферическую оболочку
На примере расчёта сферической шарнирно – опёртой оболочки по несущей способности на действие нагрузки, вызываемой равномерно распределённым давлением p, излагаются основные операции формирования разрешающих уравнений рассматриваемого метода. В соответствии с статическим методом ТПР решение поставленной задачи заключается в определении верхней границы несущей способности, которая находится из условий равновесия оболочки (13.11).
Предполагая, что в пластическом состоянии при действии давления р профиль напряжений достигает граней гиперповерхности текучести [8]
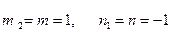 , (13.17)
, (13.17)
из уравнений равновесия можно определить усилия:
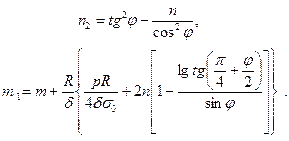
Отсюда, принимая во внимание граничное условие (шарнирное опирание контура) оболочки 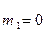 при
при 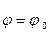 , находят
, находят
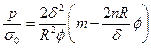 ,
,
где
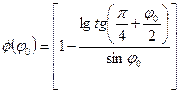 .
.
Если отношение 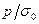 , согласно полученому выражению, больше
, согласно полученому выражению, больше 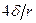 , то следует взять значения:
, то следует взять значения:
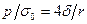 ,
, 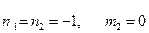 . (13.18)
. (13.18)
Очевидно, по этим формулам находят нижнюю границу предельной нагрузки.
Верхняя граница может быть определена при использовании поверхности текучести (13.16). Соответствующий параметр предельной нагрузки равен:
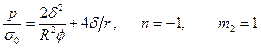 . (13.19)
. (13.19)
Теперь следует установить кинематически возможные перемещения оболочки, отвечающие ребру гиперповерхности текучести (13.17). Из ассоциированного закона течения вытекает, что деформации оболочки в состоянии пластичности равны:
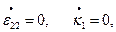
причём 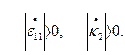
Скорости деформаций связаны со скоростями перемещений срединной поверхности в направлении нормали 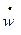 и меридиана
и меридиана 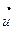 согласно (13.12)
согласно (13.12)
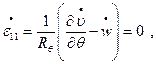
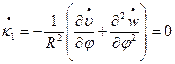 .
.
Решив систему дифференциальных уравнений при соблюдении условий:
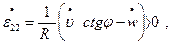
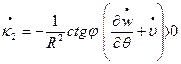 ,
,
находят поле перемещений:
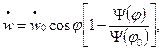
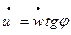 ,
,
где 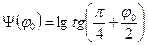 , соответствующее граничным условиям в вершине и на контуре оболочки:
, соответствующее граничным условиям в вершине и на контуре оболочки:
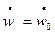 при
при 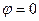 и
и 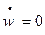 при
при 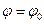 ;
; 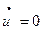 при
при 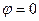 и
и 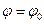 .
.
Следовательно, величины, определяемые по формулам (13.18) и (13.19), характеризуют границы диапазона значений предельного давления на сферическую оболочку с шарнирным опиранием по контуру (рис. 13.17).
Рис. 13.17
13.8. Кинематический метод определения предельного давления на сферическую оболочку c использованием линейного программирования
Наряду со статическим методом определения предельных нагрузок оболочек, на практике применяется и кинематический метод c использованием стандартных программ линейного программирования.
Указанным методом были определены предельные нагрузки плотины «Ингури ГЭС» [8], пересечения цилиндрических оболочек [13], конических и сферических оболочек. Ниже приводится пример расчёта несущей способности усечённой сферической оболочки на действие нагрузки, вызываемой давлением жёсткого штампа (рис. 13.18,а) [2]. В данном случае оболочка оказывается под воздействием кольцевой равномерно распределённой силы 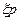 , параметр
, параметр 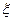 которой характеризует предельную величин нагрузки (рис. 13.18,б).
которой характеризует предельную величин нагрузки (рис. 13.18,б).
а б
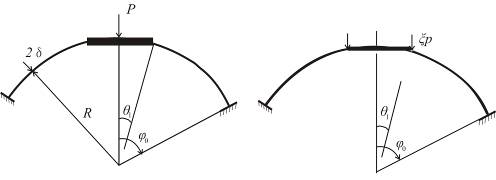
Рис. 13.18
В соответствии с кинематическим методом решение поставленной задачи заключается в определении параметра предельного давления 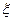 , исходя из условия достижения минимума внутренней энергии рассеяния (диссипации) оболочки, равной
, исходя из условия достижения минимума внутренней энергии рассеяния (диссипации) оболочки, равной
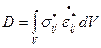 ,
,
где 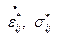 - кинематически допустимые скорости деформаций и соответствующие им напряжения (см. п. 13.5). В дальнейшем звёздочки в обозначени скорости деформаций опущены. При этом, мощность внешнего воздействия (давления Р) при скорости перемещения шайбы по вертикали
- кинематически допустимые скорости деформаций и соответствующие им напряжения (см. п. 13.5). В дальнейшем звёздочки в обозначени скорости деформаций опущены. При этом, мощность внешнего воздействия (давления Р) при скорости перемещения шайбы по вертикали 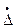 сохраняет постоянное значение
сохраняет постоянное значение 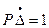 .
.
Указанный интеграл для сферической оболочки в предельном состоянии может быть представлен как сумма мощностей
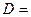
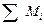
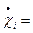
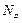
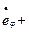
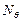
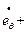
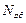
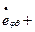
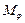
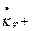
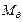
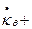
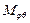
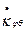 ,
,
отнесённых к единице площади срединной поверхности, поскольку интегрирование по объёму при постоянной толщине оболочки 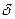 сводится к вычислению интеграла по площади. Здесь
сводится к вычислению интеграла по площади. Здесь 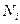 ,
, 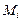 - обобщённые усилия (результирующие силы и моменты), возникающие в сечениях оболочки в меридиональном и широтном направлениях;
- обобщённые усилия (результирующие силы и моменты), возникающие в сечениях оболочки в меридиональном и широтном направлениях; 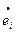 ,
, 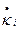 - соответствующие им скорости изменения деформаций срединной поверхности. Поскольку гиперповерхность текучести выпукла и векторы скоростей деформаций, которые находятся согласно ассоциированному закону течения, направлены по внешним нормалям на любом её участке, то величина диссипации
- соответствующие им скорости изменения деформаций срединной поверхности. Поскольку гиперповерхность текучести выпукла и векторы скоростей деформаций, которые находятся согласно ассоциированному закону течения, направлены по внешним нормалям на любом её участке, то величина диссипации 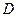 будет превышать значение мощности, накапливаемой оболочкой усилиями
будет превышать значение мощности, накапливаемой оболочкой усилиями 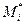 , не связанными с ассоциированным законом. Вследствие этого от равенства можно перейти к системе неравенств:
, не связанными с ассоциированным законом. Вследствие этого от равенства можно перейти к системе неравенств:
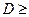
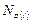
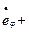
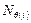
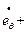
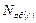
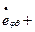
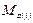
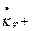
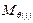
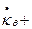
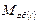
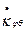
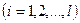 .
.
Здесь 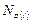 ,
, 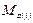 и др. - обобщённые усилия в i - ых точках кусочно – линейной гиперповерхности текучести.
и др. - обобщённые усилия в i - ых точках кусочно – линейной гиперповерхности текучести.
Для реализации численного решения рассмативаемой задачи целесообразно воспользоваться двухслойной моделью оболочки. Аналогичная модель широко используется и при анализе предельного состояния стержневых систем [10]. Как известно, величины скоростей деформаций слоёв оболочки, отстоящих на срединной поверхности на расстоянии 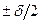 , находятся по формулам:
, находятся по формулам:
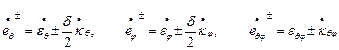 .
.
Последние связаны со скоростями перемещений сферической оболочки геометрическими соотношениями (13.12).
Диссипация энергии пластического деформирования оболочки складывается из диссипаций её слоёв
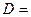
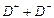 ,
,
где
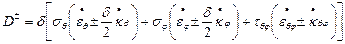 . (13.20,а)
. (13.20,а)
Как отмечено ранее, поверхность текучести Треска – Сен – Венана в случае плоского напряжённого состояния принимается линеаризованной. Поэтому энергия диссипации отдельного слоя оболочки должна удовлетворять системе неравенств:
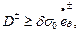
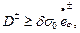
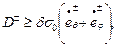
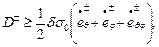
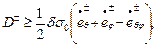 (13.20,б)
(13.20,б)
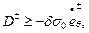
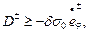
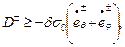
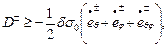
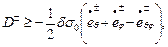
вытекающей из общего неравенства (13.20,а).
Функция цели
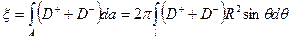
находится с учётом осевой симметрии, при этом вычисление интеграла по площади А заменяется интегрированием по образующей L.
Граничные условия оболочки на защемлённом контуре очевидны:
при 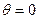 ,
, 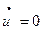 ,
, 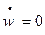 ,
, 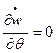 ;
;
в месте прикрепления шайбы: при 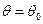 ,
, 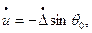
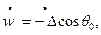
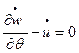 .
. 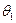 – половина центрального угла, характеризующего размер шайбы (рис. 13.19,а).
– половина центрального угла, характеризующего размер шайбы (рис. 13.19,а).
а б
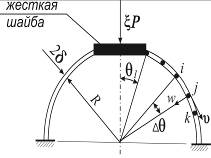
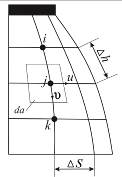
Рис. 13.19
При формировании системы равенств (13.12), неравенств (13.20,б) и функции цели в дискретной форме, которые составляют матрицу метода линейного программирования, срединная поверхность оболочки разбивается сеткой на малые площадки 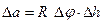 , где
, где 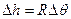 - шаг сетки по меридиану (рис. 13.19,б). Скорости деформаций слоёв оболочки (13.13) определяют в узловых точках сетки разбиения с помощью конечных разностей и выражают через скорости перемещений (13.12). Замена производных скоростей перемещений
- шаг сетки по меридиану (рис. 13.19,б). Скорости деформаций слоёв оболочки (13.13) определяют в узловых точках сетки разбиения с помощью конечных разностей и выражают через скорости перемещений (13.12). Замена производных скоростей перемещений 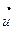 и
и 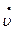 выполняется левыми и правыми конечными разностями, а производных прогиба
выполняется левыми и правыми конечными разностями, а производных прогиба 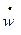 – центральными.
– центральными.
Численные расчёты производились с использованием программы симплекс- метода для трёх оболочек различных размеров. Результаты расчётов приводятся в табл. 13.1.
Таблица13.1
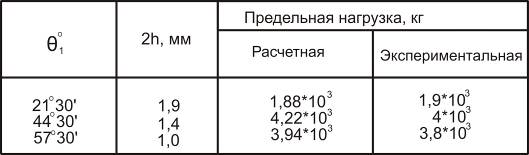
Достоверность результатов теоретических исследований подтверждена серией экспериментов, проведённых в Радиотехническом НИИ в 1977-78гг. Базловым В. П. Как в экспериментах, так и в расчётах выяснилось, что пластическая зона локализуется вблизи места примыкания шайбы к оболочке (рис. 13.20). При этом размеры экспериментально обнаруженной зоны пластических деформаций отличались от расчётных всего лишь на 1-2 мм. Распределение перемещений в этом месте показано штриховкой.
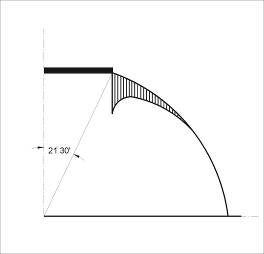
Рис. 13.20
13.9. Динамика сферических оболочек с учётом
пластичности материала
В заключение приводятся результаты исследования предельного сопротивления сферической оболочки, нагруженной равномерным давлением р высокой интенсивности в течение короткого интервала времени  (рис. 13.21) [8].
(рис. 13.21) [8].
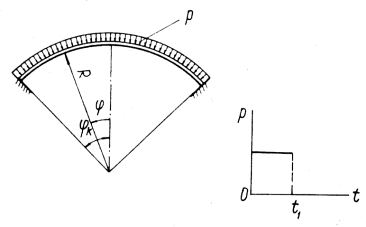
Рис. 13.21
Постоянное внешнее давление р, действующее по нормали к поверхности оболочки, прикладывается в момент времени t=0 и при t= 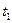 снимается. Напряженное состояние в оболочке соответствует определенным участкам поверхности текучести, показанной на рис. 13.16. Деформации определяются на основе ассоциированного закона течения.
снимается. Напряженное состояние в оболочке соответствует определенным участкам поверхности текучести, показанной на рис. 13.16. Деформации определяются на основе ассоциированного закона течения.
Уравнения движения сферической оболочки, нагруженной нормальным давлением р, имеют вид [8]:
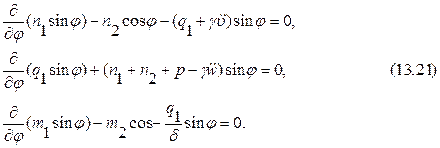
В отличие от условий равновесия (13.11), в уравнениях движения имеются слагаемые 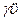 ,
, 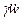 , характеризующие силы инерции оболочки в касательной плоскости. Кроме того, добавлен новый параметр
, характеризующие силы инерции оболочки в касательной плоскости. Кроме того, добавлен новый параметр 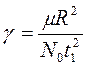 , носящий комбинированный смысл. Он содержит как физико- механические характеристики оболочки:
, носящий комбинированный смысл. Он содержит как физико- механические характеристики оболочки: 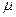 - плотность материала,
- плотность материала, 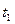 - длительность действия нагрузки,
- длительность действия нагрузки, 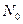 - предельное значение усилия на единицу длины элемента в сечении срединной поверхности, так и геометрические размеры оболочки
- предельное значение усилия на единицу длины элемента в сечении срединной поверхности, так и геометрические размеры оболочки 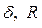 .
.
Деформации оболочки определяются по формулам [8]:
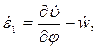
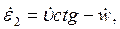 (13,21,а)
(13,21,а)
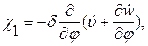
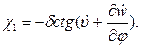 (13,21,б)
(13,21,б)
Нагрузка р, прикладываемая к оболочке, должна несколько превышать разрушающую (статическую), иначе движение не возникает вовсе, поскольку в исследовании принята модель жёсткопластического деформирования материала оболочки. Для значений р, немного больших, чем разрушающее давление р0, следует ожидать, что напряженное состояние оболочки будет соответствовать тем же участкам поверхности текучести, что и при статическом решении задачи. Следовательно, в центральной зоне оболочки (при 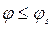 ) распределение усилий и моментов соответствует ребру линеаризованной поверхности текучести (описанной около точной) [8]:
) распределение усилий и моментов соответствует ребру линеаризованной поверхности текучести (описанной около точной) [8]:
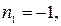
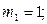
в пограничной зоне
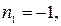
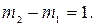
Следует различать две фазы движения оболочки: фазу нагружения (интервал времени 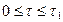 ) и фазу разгрузки (интервал
) и фазу разгрузки (интервал 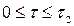 ).
).
Фаза 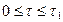 . В соответствии с ассоциированным законом течения и формулами скоростей деформации и изменения кривизн (13.22) в статике нетрудно получить выражение прогиба
. В соответствии с ассоциированным законом течения и формулами скоростей деформации и изменения кривизн (13.22) в статике нетрудно получить выражение прогиба 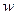 и меридионального смещения
и меридионального смещения 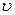 по зонам, которые можно принять в качестве кинематически возможных при “среднем” уровне динамической нагрузки:
по зонам, которые можно принять в качестве кинематически возможных при “среднем” уровне динамической нагрузки:
в диапазоне углов 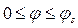
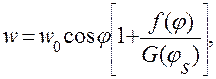 (13,22а)
(13,22а)
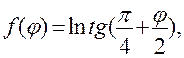
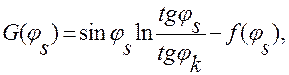
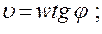 (13.22,б)
(13.22,б)
в зоне 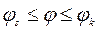
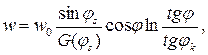 (13.23,а)
(13.23,а)
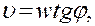 (13.23,б)
(13.23,б)
где 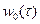 – функция прогиба центра оболочки;
– функция прогиба центра оболочки;
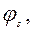
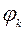 - значения углов, соответствующие границе зон и опорному контуру оболочки. Выражения для перемещений удовлетворяют краевому условию
- значения углов, соответствующие границе зон и опорному контуру оболочки. Выражения для перемещений удовлетворяют краевому условию
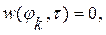
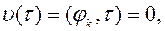
условию совместности деформаций на границе зон, а также начальным условиям
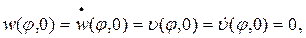
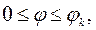
если считать 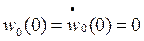 . Принимая во внимание (13.7), из уравнений движения (13.21) можно найти усилия
. Принимая во внимание (13.7), из уравнений движения (13.21) можно найти усилия 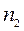 ,
, 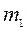 в зоне
в зоне 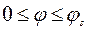
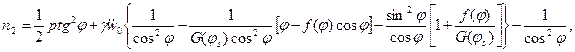 (13.24)
(13.24)
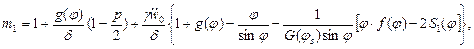 (13.25)
(13.25)
где использованы функция 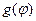 и степенной ряд
и степенной ряд 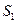 :
:
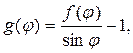
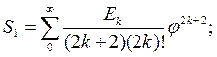
здесь 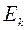 - числа Эйлера.
- числа Эйлера.
На границе зон 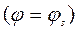 имеет место
имеет место 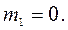
Тогда из (13.25) следует
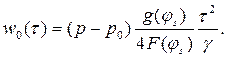 (13.26)
(13.26)
Здесь F 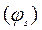 - выражение, содержащееся в фигурных скобках (13.25) при значении
- выражение, содержащееся в фигурных скобках (13.25) при значении 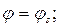
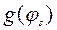 - значение функции
- значение функции 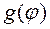 при
при 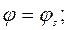
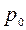 - предельная нагрузка в данной оболочке (в дальнейших расчетах принимается минимум “верхней границы” по [8]). Вследствие непрерывности усилий
- предельная нагрузка в данной оболочке (в дальнейших расчетах принимается минимум “верхней границы” по [8]). Вследствие непрерывности усилий 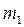 и
и 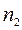 на границе зон, из уравнений (13.21) с учетом (13.25) нетрудно найти их распределение в приопорной зоне
на границе зон, из уравнений (13.21) с учетом (13.25) нетрудно найти их распределение в приопорной зоне
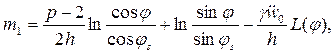 (13.27)
(13.27)
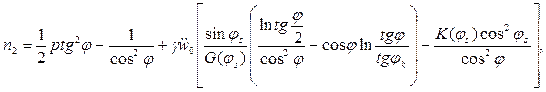 (13.28)
(13.28)
где
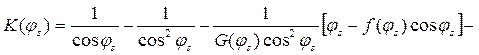
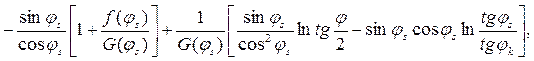
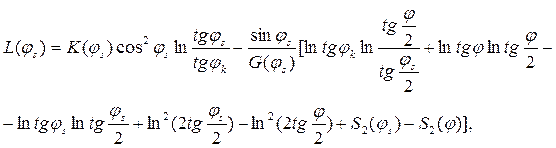
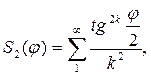
где 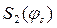 - обозначение одноименного ряда при
- обозначение одноименного ряда при 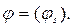
Граница зон различных напряженных состояний в оболочке определяется уравнением
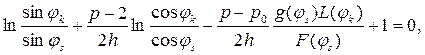
полученным из (13.28) с учетом (13.27) и условия 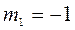 на контуре.
на контуре.
Фаза 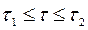 . В этой фазе нагрузка снимается.
. В этой фазе нагрузка снимается.
Вследствие пластического рассеивания энергии движение становится затухающим. При этом форма движения оболочки сохраняется непрерывной. Следовательно, в зоне 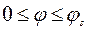 поле скоростей по-прежнему имеет вид (13.22), однако граница зон
поле скоростей по-прежнему имеет вид (13.22), однако граница зон 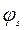 движется; теперь она является функцией времени.
движется; теперь она является функцией времени.
Находя компоненты ускорения и принимая во внимание 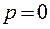 , из уравнений движения (13.21) с учетом граничных условий в вершине оболочки получаем:
, из уравнений движения (13.21) с учетом граничных условий в вершине оболочки получаем:
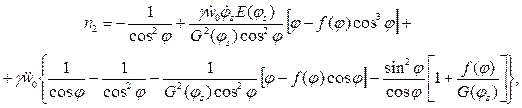 (13.29)
(13.29)
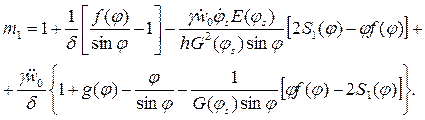 (13.30)
(13.30)
Аналогично находят распределение усилий и в приопорной зоне 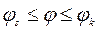
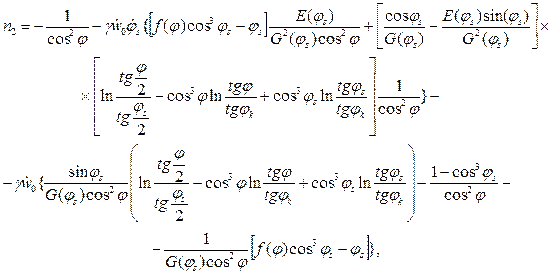 (13.31)
(13.31)
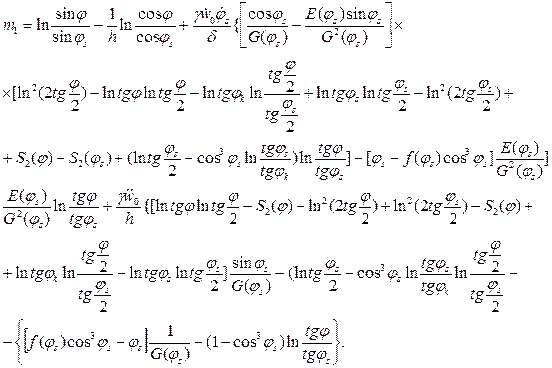 (13.32)
(13.32)
Здесь функция 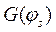 по-прежнему определяется по формуле (13.22), а функция
по-прежнему определяется по формуле (13.22), а функция 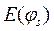 имеет следующий вид
имеет следующий вид
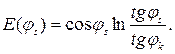
Воспользовавшись условием равенства 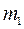 , определяемого по (13.22), нулю при
, определяемого по (13.22), нулю при 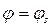 и граничным условием
и граничным условием 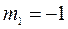 при
при 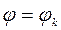 , выводят основные уравнения, характеризующие движение оболочки в фазе разгрузки:
, выводят основные уравнения, характеризующие движение оболочки в фазе разгрузки:
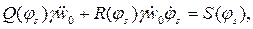
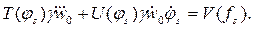
Отсюда, решив полученную систему уравнений, находят скорость и ускорение границы:
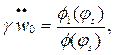
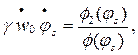 (13.33)
(13.33)
где
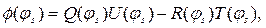
- множители перед 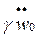 и
и 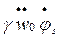 в выражениях для
в выражениях для 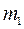 (формулы (13.22), (13.33)) при значениях
(формулы (13.22), (13.33)) при значениях 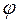 ,
, 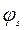 и
и 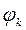 ;
; 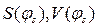 - свободные члены в указанных формулах при
- свободные члены в указанных формулах при 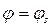 и
и 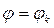 .
.
Полагая 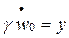 , выражения (13.33) приводят к сокращённой форме:
, выражения (13.33) приводят к сокращённой форме:
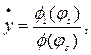 (13.34)
(13.34)
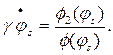 (13.35)
(13.35)
Система двух последних уравнений сводится к одному дифференциальному уравнению
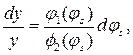
решение которого с учетом начальных условий имеет вид
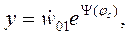 (13.36)
(13.36)
где 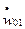 - скорость прогиба вершины оболочки в момент
- скорость прогиба вершины оболочки в момент 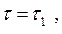
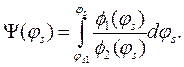 (13.37)
(13.37)
Из (13.35) скорость движения границы зон 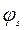 различных напряженных состояний определяется формулой
различных напряженных состояний определяется формулой
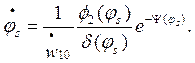 (13.38)
(13.38)
Положение границы зон
