Основные теоремы и принципы электромагнитного поля
Электродинамические потенциалы электромагнитного поля.
К электродинамическим потенциалам электромагнитного поля относят:
- векторный магнитный потенциал 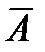
- электрический скалярный потенциал 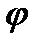
- скалярный магнитный потенциал 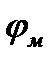
- электрический векторный потенциал.
Векторный магнитный потенциал определяется как 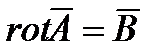 или
или 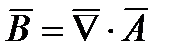 ((х) векторное произведение).
((х) векторное произведение).
Электрический скалярный потенциал 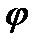 - некоторая скалярная величина, градиент которой равен сумме векторов напряженности электрического поля и производной по времени от магнитного векторного потенциала
- некоторая скалярная величина, градиент которой равен сумме векторов напряженности электрического поля и производной по времени от магнитного векторного потенциала
 или
или 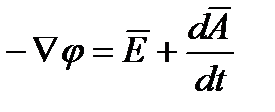
Доказательство:
 или
или 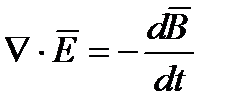 или
или 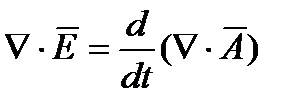
При этом 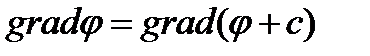 , с – некоторая постоянная величина.
, с – некоторая постоянная величина.
Связь векторного магнитного потенциала с электрическим скалярным потенциалом.
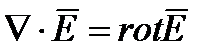
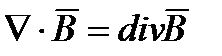
Запишем первое уравнение Максвелла в дифференциальной форме:
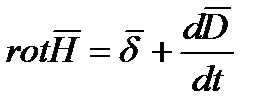 или
или 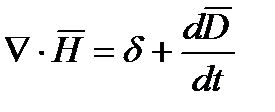
Заменим в этом уравнении напряженность магнитного поля H и электрическое смещение D на векторный магнитный и электрический потенциалы. Получим
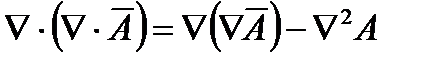 ************
************
Окончательно
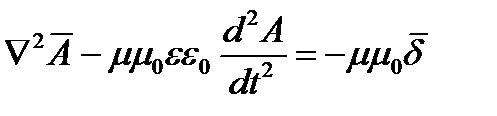
Для частного случая, не изменяющихся во времени полей
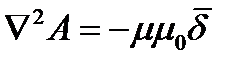
Это уравнение называется уравнением Пуассона для векторного магнитного потенциала.
А совокупность уравнений:
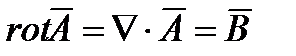
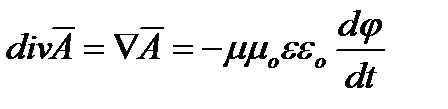
Является системой уравнений при помощи, которых мы вводим новое векторное поле. Аналогично могут быть введены и другие потенциалы: скалярный магнитный и электрический векторный.
Запись системы уравнений Максвелла через скалярный электрический и векторный магнитный потенциалы:

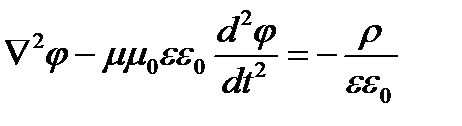
Удобства этой формы записи состоит в том, что переменные здесь разделены при чем каждая из уравнений содержит только одну переменную. Первые части этих уравнений представляют собой источники возбуждающие электромагнитное поле – токи или заряды.
Решение уравнений Максвелла при заданных источниках.
Пусть в некоторой области пространства нет частиц, способных переносить заряды и поляризоваться 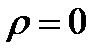 ,
, 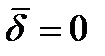 и
и 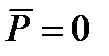 . назовем такую среду вакуумом. Система уравнений Максвелла для такого пространства будет иметь вид.
. назовем такую среду вакуумом. Система уравнений Максвелла для такого пространства будет иметь вид.
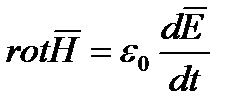
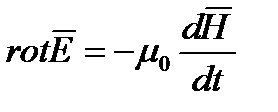
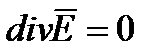
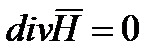
Известно, что основное уравнение поля можно записать через электродинамические потенциалы A и 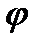 . Для области пространства, где нет зарядов, можно принять
. Для области пространства, где нет зарядов, можно принять 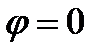 .
.
В этом случае уравнение для векторного потенциала можно записать в виде
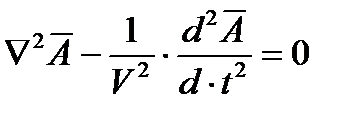
, где 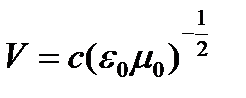 - скорость света
- скорость света
Уравнения такой структуры называют волновыми уравнениями, а их решение волнами. Если найдено решение A - то можно найти напряженность электрического и магнитного полей.
Из выражения 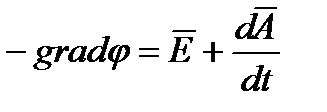 и
и  , учитывая, что
, учитывая, что 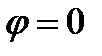 и
и 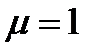 для вакуума получим
для вакуума получим
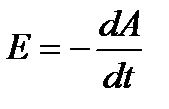 и
и 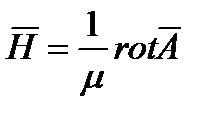
В некоторых случаях удобнее искать решение уравнений непосредственно записанных для векторов 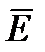 и
и 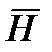 .
.
Такие уравнения получаются из (1), исключив один из неизвестных. Например, если вынести ротор левой и правой части второго уравнения то получим
 или
или
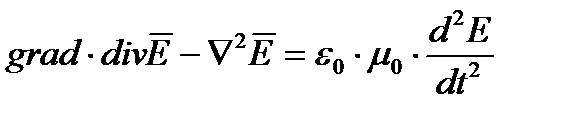
К левой части применено известное правило векторного анализа 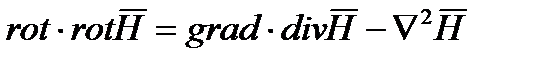 , а в правой части сделана подстановка из 1-го уравнения
, а в правой части сделана подстановка из 1-го уравнения

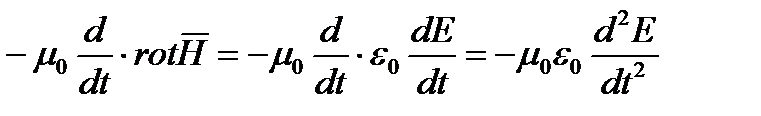
Учитывая, что 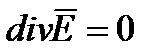 - можно получить
- можно получить
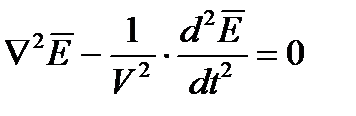 и аналогично
и аналогично
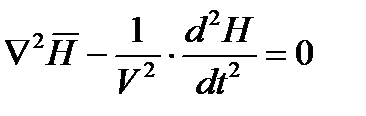
Это есть система волновых уравнений.
Решение волновых уравнений для заданных источников.
Для тока или напряжения в однородной линии без потерь структура уравнения имеет вид 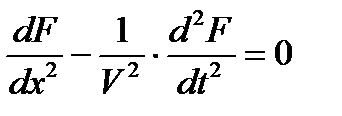 , а его решение как сумма двух волн: падающей и обратной.
, а его решение как сумма двух волн: падающей и обратной.
Решение записывается в виде 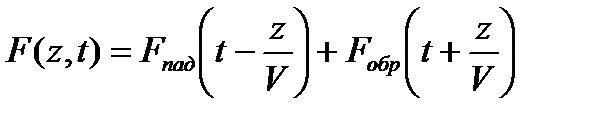
Падающая волна  распространяется в направлении оси
распространяется в направлении оси 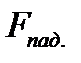 , обратная
, обратная 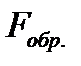 - в обратном направлении.
- в обратном направлении.
Положим, что векторный потенциал A применяется только по направлению оси z. Такая волна называется плоской электромагнитной волной. Волновое уравнение в этом случае будет иметь вид  (2)
(2)
Решение уравнения (2) будет иметь вид:
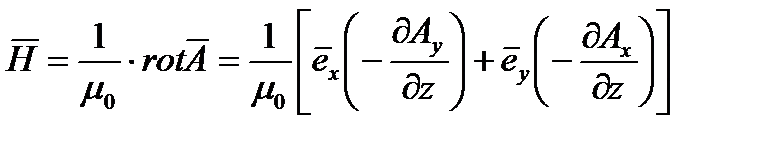
Где 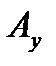 - проекция А на ось y
- проекция А на ось y
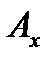 - проекция А на ось x
- проекция А на ось x
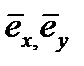 - орты.
- орты.
То есть вектор 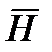 не имеет z составляющей. Вектор H выражается через Е
не имеет z составляющей. Вектор H выражается через Е
В случае плоской электромагнитной волны векторы Е и Н лежат в плоскости 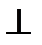 к оси Z. И для прямой обратной волны
к оси Z. И для прямой обратной волны

Переменное электромагнитное поле в однородной проводящей среде.
1. Уравнение Максвелла для проводящей среды.
Рассмотрим особенности распространения электромагнитной волны в проводящей среде с проводимостью 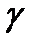 и магнитной проницаемостью
и магнитной проницаемостью 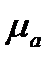 .
. 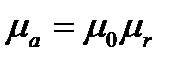 ;
; 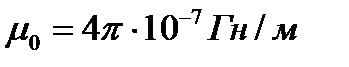
Первое и второе уравнение Максвелла записанное в комплексной форме для синусоидально изменяющихся во времени 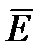 и
и 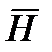 .
.
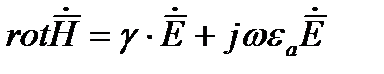 (1)
(1)
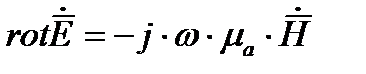 (2)
(2)
где 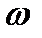 - круговая частота изменения векторов
- круговая частота изменения векторов 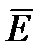 и
и 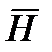
В проводящей среде даже при очень высоких частотах
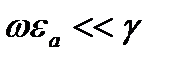
По этому с большой степенью точности слагаемым 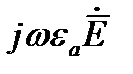 в первом уравнении Максвелла можно пренебречь. Таким образом первое и второе уравнение Максвелла для проводящих сред записываются как
в первом уравнении Максвелла можно пренебречь. Таким образом первое и второе уравнение Максвелла для проводящих сред записываются как
(1) 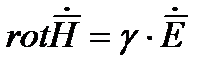
(2) 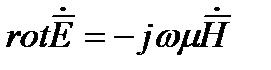
Решим эти уравнения относительно 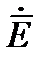 и
и 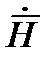 . С этой целью возьмем ротор от (1)
. С этой целью возьмем ротор от (1)
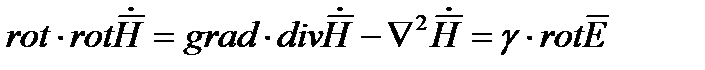
Учтем, что 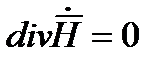 , поэтому
, поэтому 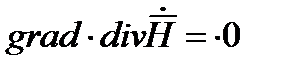 . Вместо
. Вместо 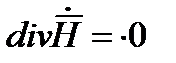 в соответствие с (2) подставим -.
в соответствие с (2) подставим -. 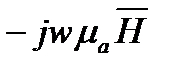 Получим
Получим
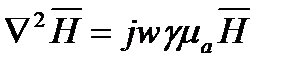 (3)
(3)
Данное уравнение является дифференциальным относительно  .
.
В общем случае, когда 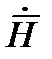 зависит от всех трех или даже от двух координат, решение этого уравнения очень сложно. Ограничимся рассмотрением решения данного уравнения для плоской электромагнитной волны.
зависит от всех трех или даже от двух координат, решение этого уравнения очень сложно. Ограничимся рассмотрением решения данного уравнения для плоской электромагнитной волны.
2. Плоская электромагнитная волна.
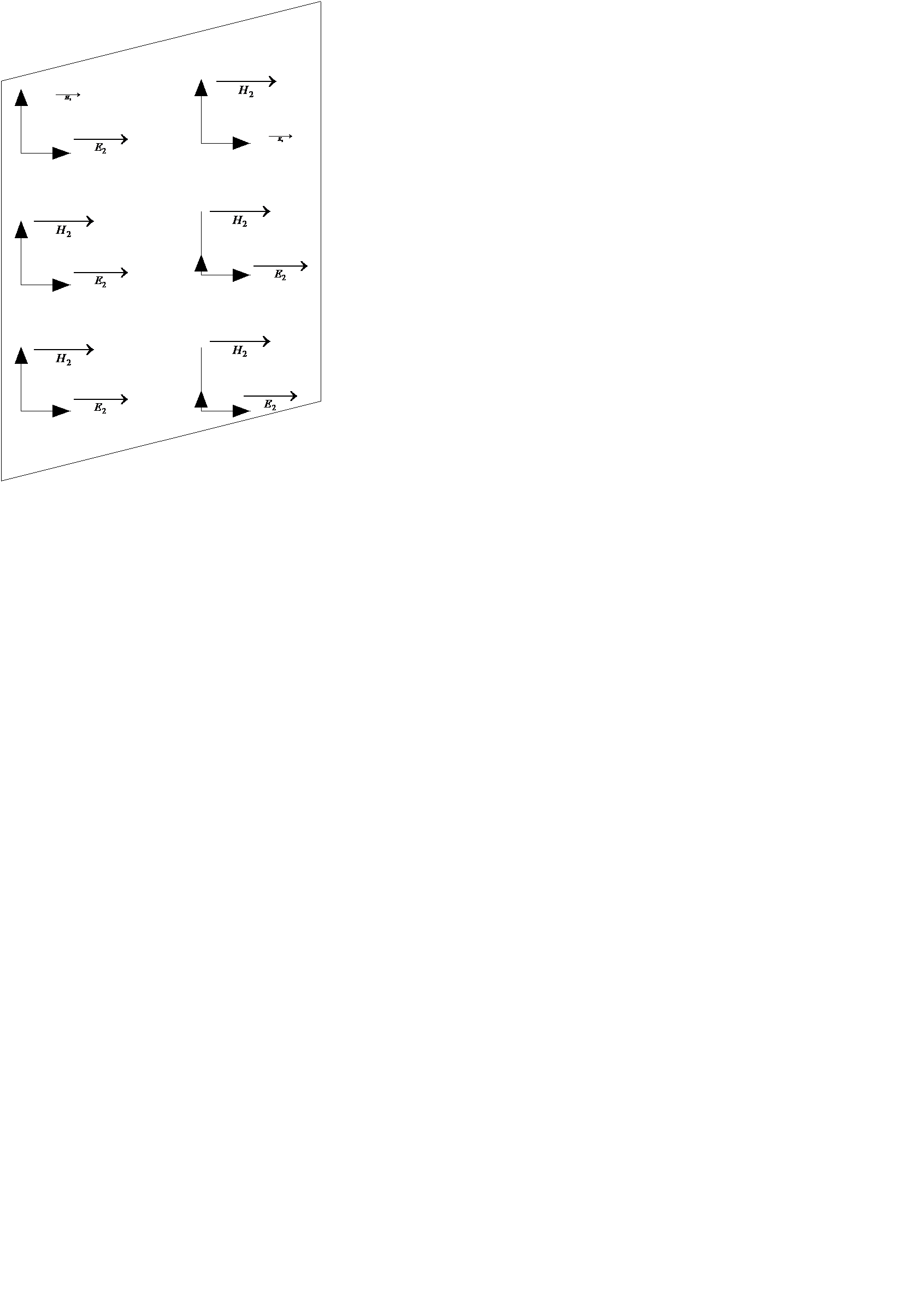 В общем случае под плоской электромагнитной волной понимают волну, векторы
В общем случае под плоской электромагнитной волной понимают волну, векторы 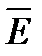 и
и 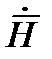 которые расположены в плоскости x o y , перпендикулярны направлению распространения волны ( ось z) и изменяющиеся только функции координаты z и времени t.
которые расположены в плоскости x o y , перпендикулярны направлению распространения волны ( ось z) и изменяющиеся только функции координаты z и времени t.
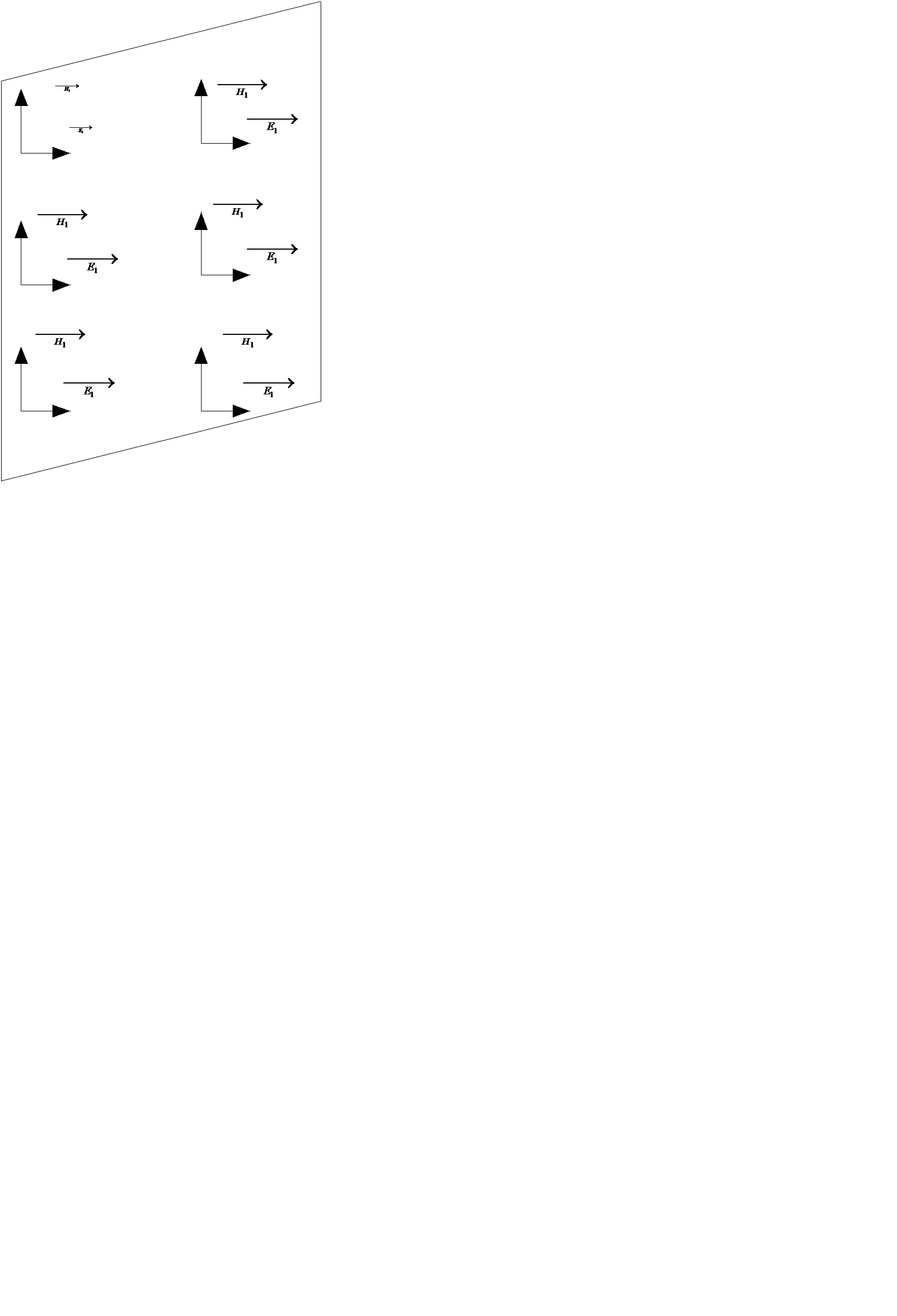
Рис.
На рисунке изображены для одного и того же момента времени векторы 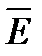 и
и 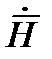 в двух параллельных плоскостях , перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости напряженности электрического и магнитных полей одинаковы по величине и направлении. Во всех точках второй плоскости напряженность электрического и магнитного полей также одинаковы по величине и направлению, но не равна напряженности поля в первой плоскости.
в двух параллельных плоскостях , перпендикулярных оси z декартовой системы координат. Во всех точках первой плоскости напряженности электрического и магнитных полей одинаковы по величине и направлении. Во всех точках второй плоскости напряженность электрического и магнитного полей также одинаковы по величине и направлению, но не равна напряженности поля в первой плоскости.
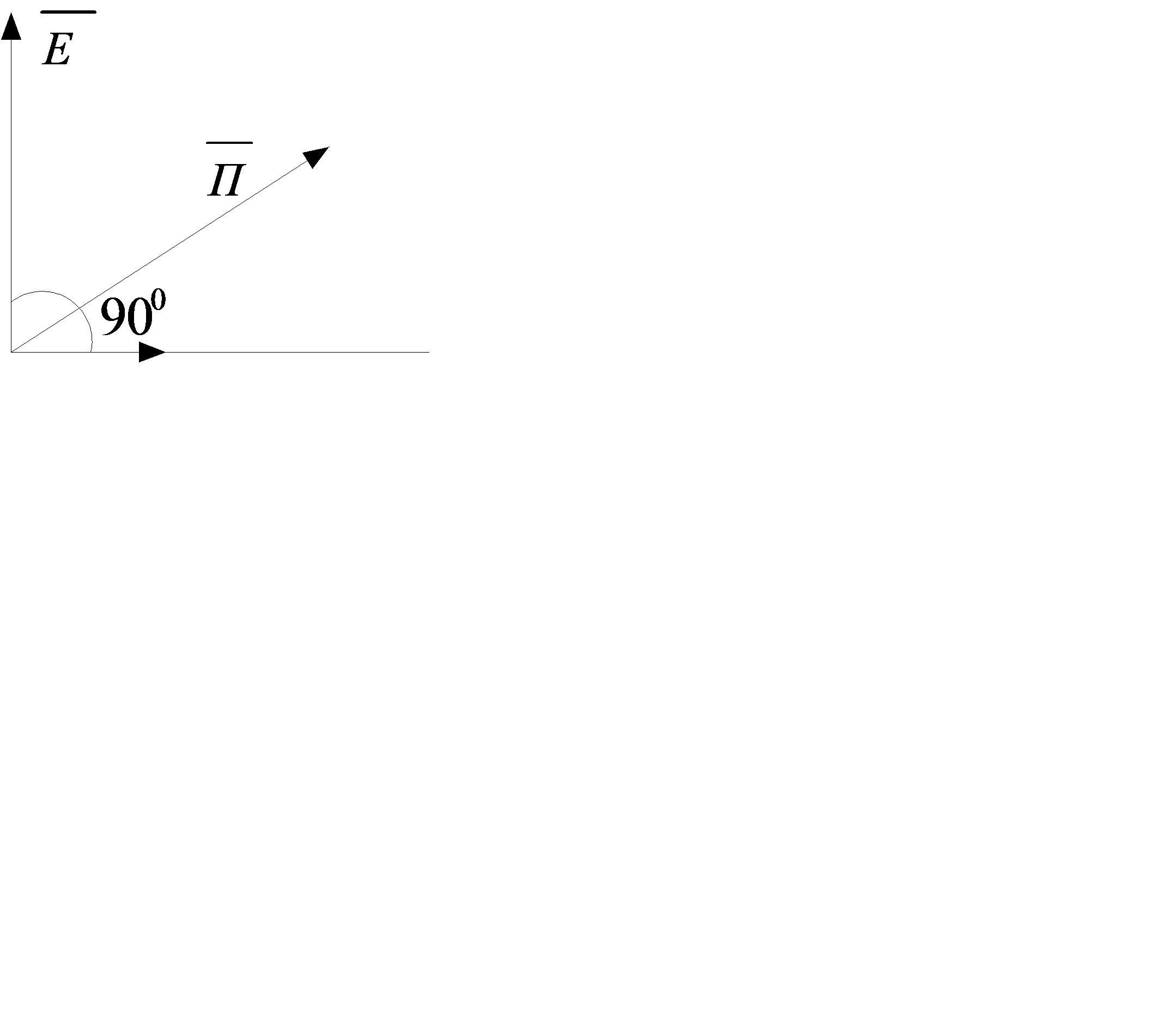 В плоской электромагнитной волне между векторами
В плоской электромагнитной волне между векторами 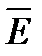 и
и 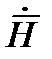 существует пространственный сдвиг в 900.
существует пространственный сдвиг в 900.
Характеристика сред , связывающая абсолютную магнитную проницаемость , удельную проводимость 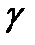 [Сим/м] , угловую чистоту
[Сим/м] , угловую чистоту 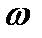 называется волновым сопротивлением проводящей среды
называется волновым сопротивлением проводящей среды
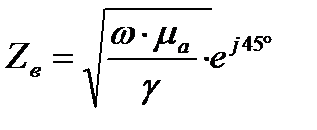 [Ом]
[Ом]
Волновое сопротивление 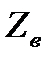 можно трактовать как отношение
можно трактовать как отношение 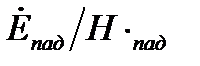 , при этом сдвиг по времени между
, при этом сдвиг по времени между 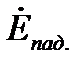 и
и 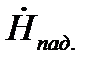 для одной и той же точки поля равен 450 .
для одной и той же точки поля равен 450 .
| <== предыдущая лекция | | | следующая лекция ==> |
| Электромагнитные волны. Из уравнений Максвелла следует важный вывод о существовании принципиально нового физического явления: электромагнитное поле способно существовать | | | Автогенді үрдістер. |
Дата добавления: 2015-12-16; просмотров: 1663;
