Запись на языке логики предикатов различных предложений
Уделим немного внимания применению одного из аспектов логики предикатов – грамотной записи на языке логики предикатов различных математических предложений. Это будет весьма полезным студенту и будущему учителю не только для формирования логической культуры, но и для практического оперирования рассматриваемыми понятиями и методами непосредственно в процессе изучения математических дисциплин в вузе и преподавания математики в школе.
С помощью кванторной символики удобно записывать формулировки различных определений и теорем. В процессе такой записи приходится осмысливать данное предложение, отчетливо выделять в нем посылки и заключение (если это теорема), очерчивать более широкий круг понятий и четко выделять ограничивающее условие (если это определение). Одним словом, перевод расплывчатой словесной формулировки на строгий язык логики предикатов, не допускающий противоречивых толкований, способствует четкости и ясности мышления. Рассмотрим некоторые примеры.
Пример 1. Определение предела последовательности: «Число а называется пределом последовательности 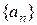 , если для всякого положительного действительного числа
, если для всякого положительного действительного числа 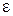 существует такое натуральное число
существует такое натуральное число 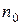 , что для всякого натурального n, большего
, что для всякого натурального n, большего 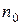 , имеет место
, имеет место 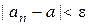 » на языке логики предикатов записывается так:
» на языке логики предикатов записывается так:
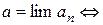
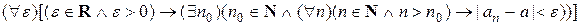 .
.
Используя символику ограниченных кванторов, это определение можно записать компактнее:
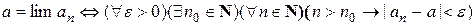 .
.
Нередко требуется доказать, что некоторое число a не является пределом последовательности 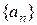 , т.е.
, т.е. 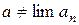 . Для доказательства нужно построить утверждение, являющееся отрицанием сформулированного определения. Поможет в этом логика предикатов. Используя равносильности логики предикатов, преобразуем отрицание исходной формулы к приведенному виду:
. Для доказательства нужно построить утверждение, являющееся отрицанием сформулированного определения. Поможет в этом логика предикатов. Используя равносильности логики предикатов, преобразуем отрицание исходной формулы к приведенному виду:
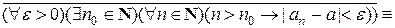
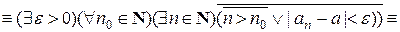
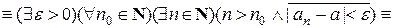
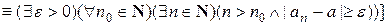
(здесь на первом шаге воспользовались законом де Моргана для кванторов и законом исключения импликации, на втором – законом де Моргана для дизъюнкции и законом двойного отрицания, на третьем – правилом отрицания неравенства).
Таким образом, утверждение: «Число 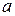 не является пределом последовательности
не является пределом последовательности 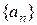 » раскрывается так: «Существует такое положительное число
» раскрывается так: «Существует такое положительное число 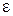 , что для всякого натурального числа
, что для всякого натурального числа 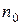 найдется такое натуральное число
найдется такое натуральное число 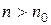 , что
, что 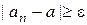 ». Несходимость последовательности
». Несходимость последовательности 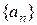 означает, что никакое число не является ее пределом, т.е.
означает, что никакое число не является ее пределом, т.е. 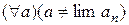 . Это вместе с полученным утверждением дает
. Это вместе с полученным утверждением дает
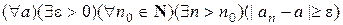 .
.
Пример 2. Определение простого числа: «Натуральное число х называется простым, если оно не равно 1 и имеет ровно два натуральных делителя 1 и х» на языке логики предикатов запишется так:
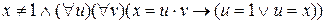 .
.
Отрицание этого утверждения, т.е. утверждение о том, что «число 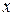 не является простым», записывается следующим образом:
не является простым», записывается следующим образом:
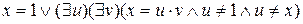 .
.
Определение составного числа на языке логики предикатов будет выглядеть так:
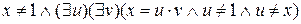 .
.
Предлагается самостоятельно разобраться в составлении последнего утверждения.
Пример 3. Определение: «Точка 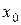 из области определения функции
из области определения функции 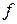 называется точкой максимума функции
называется точкой максимума функции 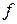 , если существует такая δ‑окрестность данной точки, что для всех x из данной окрестности
, если существует такая δ‑окрестность данной точки, что для всех x из данной окрестности 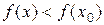 » на языке логики предикатов запишется так:
» на языке логики предикатов запишется так:
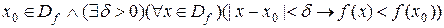 .
.
Запишите самостоятельно отрицание данного утверждения.
Вопросы для самоконтроля по теме «Логика предикатов»
1. Что понимается под предикатом, его областью определения и множеством истинности? Определить тождественно истинный (ложный) предикат.
2. Найдите множества истинности предикатов и изобразите их на координатной прямой:
а) 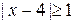 ;
;
б) 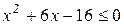 ;
;
в) 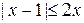 .
.
3. Что понимается под квантором общности и существования? Определите операции навешивания этих кванторов на одноместный предикат.
4. Определите операции над предикатами.
5. Что понимается под предикатной формулой?
6. Сформулируйте правило отрицания выражений, начинающихся с кванторов.
7. Определите понятие равносильности предикатов. Выясните, равносильны ли предикаты 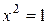 и
и 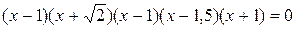 над множеством Z целых чисел?
над множеством Z целых чисел?
8. Пользуясь законом контрапозиции, докажите теоремы:
а) если 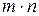 – нечетное число, то
– нечетное число, то 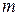 и
и 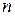 нечетные числа (
нечетные числа ( 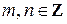 );
);
б) если 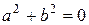 , то
, то 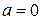 или
или 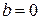 (
( 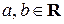 ).
).
9. Докажите методом от противного теорему: «Если прямая 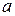 , лежащая вне плоскости, параллельна прямой
, лежащая вне плоскости, параллельна прямой 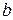 , лежащей в плоскости
, лежащей в плоскости 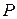 , то прямая
, то прямая 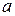 параллельна плоскости
параллельна плоскости 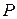 ». Укажите соответствующую схему.
». Укажите соответствующую схему.
10. Для теоремы: "Если целое число 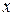 делится на 15, то
делится на 15, то 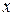 делится и на 3, и на 5". Составить формулу, соответствующую ее логической структуре, и найти обратную, противоположную и противоположную обратной теоремы.
делится и на 3, и на 5". Составить формулу, соответствующую ее логической структуре, и найти обратную, противоположную и противоположную обратной теоремы.
11. Выделить этапы доказательства методом математической индукции. Доказать, что для любого натурального 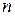
a) 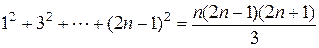 ;
;
б) 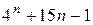 делится на 9;
делится на 9;
в) 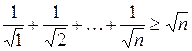 .
.
Дата добавления: 2015-11-04; просмотров: 5023;
