Решение задач линейного программирования с использованием программы Optimization Toolbox. Часть 2. Транспортная задача и задача усреднения состава руды.
Основной задачей линейного программирования является минимизация (или максимизация) линейной формы от нескольких аргументов  при наличии нескольких ограничений (неравенств или равенств), представляющих собой также линейные формы от указанных аргументов. В большинстве случаев аргументы принимаются неотрицательными. К числу задач, решаемых методом линейного программирования, относится транспортная задача.
при наличии нескольких ограничений (неравенств или равенств), представляющих собой также линейные формы от указанных аргументов. В большинстве случаев аргументы принимаются неотрицательными. К числу задач, решаемых методом линейного программирования, относится транспортная задача.
Пример 3. Транспортная задача. У компании есть 2 завода и три оптовых магазина-склада. Первый завод может поставлять не более 100 единиц продукции в неделю, второй – не более 200 единиц. В первом магазине-складе может храниться не более 150 единиц продукции, во втором – 200 единиц, в третьем – 350 единиц. Цена продажи единицы продукции в первом магазине 12$, во втором 14$, в третьем 15$. Суммарные затраты на производство и доставку единицы продукции с первого завода в первый, второй и третий магазины составляют соответственно 8, 10 и 12$, а со второго завода 7, 9 и 11$.
В таблице 1 показаны разность между ценой продукции и суммарными затратами на производство продукции на заводе i и доставку её в магазин j, и произведение количества завозимой продукции  на эту разность, определяющую прибыль от реализации продукции. Компания хочет определить, сколько единиц продукции нужно отправить с каждого завода каждому магазину, чтобы максимизировать прибыль.
на эту разность, определяющую прибыль от реализации продукции. Компания хочет определить, сколько единиц продукции нужно отправить с каждого завода каждому магазину, чтобы максимизировать прибыль.
Таблица 1.
| Магазин 1 | Магазин 2 | Магазин 3 | |
| Завод 1 |  * 4;
4 = 12 – 8; * 4;
4 = 12 – 8;
|  * 4;
4 = 14 – 10; * 4;
4 = 14 – 10;
| 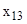 * 3;
3 = 15 –12; * 3;
3 = 15 –12;
|
| Завод 2 |  * 5;
5 = 12 – 7; * 5;
5 = 12 – 7;
|  * 5;
5 = 14 – 9; * 5;
5 = 14 – 9;
|  * 4;
4 = 15 – 11; * 4;
4 = 15 – 11;
|
Математическое описание задачи:
4  + 5
+ 5  + 4
+ 4  + 5
+ 5  + 3
+ 3 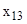 + 4
+ 4 
 max;
max;
 +
+  +
+ 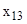
 100 (производственная мощность первого завода);
100 (производственная мощность первого завода);
 +
+  +
+ 
 200 (производственная мощность второго завода);
200 (производственная мощность второго завода);
 +
+ 
 150 (ограничение для первого магазина);
150 (ограничение для первого магазина);
 +
+ 
 200 (ограничение для второго магазина);
200 (ограничение для второго магазина);
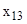 +
+ 
 350 (ограничение для третьего магазина);
350 (ограничение для третьего магазина);

 0.
0.
Специфическая форма транспортной задачи: все коэффициенты при  в ограничениях равны 1. Транспортная задача входит в особый класс задач линейного программирования,
в ограничениях равны 1. Транспортная задача входит в особый класс задач линейного программирования,
называемый сетевыми задачами.
Приведя математическое описание к стандартному (для программы Optimization Toolbox) виду, получим (введены обозначения  =
=  ;
;  =
=  ;
;  =
=  ;
;  =
=  ;
; 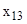 =
= 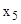 ;
;
 =
=  ):
):
- 4  - 5
- 5  - 4
- 4  - 5
- 5  - 3
- 3 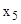 - 4
- 4 
 min;
min;
 +
+  +
+ 
 100;
100;
 +
+  +
+ 
 200;
200;
 +
+ 
 150;
150;
 +
+ 
 200;
200;
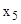 +
+ 
 350;
350;

 0;
0; 
 0;
0; 
 0;
0; 
 0;
0; 
 0;
0; 
 0;
0;
В рабочем окне программы Matlab выполняем действия, приведенные ниже
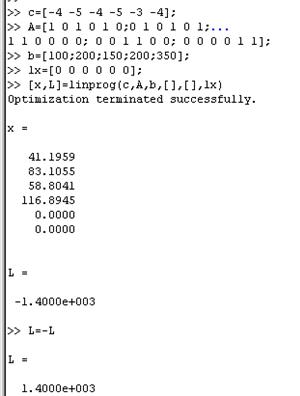 Решение задачи показывает, что третий магазин не нужно использовать, если требуется максимизировать прибыль. Максимум прибыли составляет 1400$.
Решение задачи показывает, что третий магазин не нужно использовать, если требуется максимизировать прибыль. Максимум прибыли составляет 1400$.
Дробные значения x трактуем как математическое ожидание недельных показателей.
Пример 4. Задача об усреднении состава руды.
Железная руда поступает в бункер из четырёх рудников. Для получения из неё сплава
с заданными свойствами она должна содержать три элемента А, В и С в количестве, указанном в таблице 1
Таблица 1
| Элемент | Минимальное содержание |
| А | 5 кг/т |
| В | 100 кг/т |
| С | 30 кг/т |
Руда на каждом руднике содержит эти три элемента в разных количествах (кг/т), указанных в таблице 2.
Таблица 2
| Элемент сплава | Рудник | |||
| А | ||||
| В | ||||
| С |
Стоимость добычи и перевозки 1 т руды от рудника до бункера указана в таблице 3 ($).
Таблица 3
| Рудник | Стоимость добычи и перевозки |
Можно составить различные смеси, удовлетворяющие минимальным требованиям по всем основным элементам. Но руда от разных рудников имеет различную стоимость, поэтому стоимость смесей также различна. Требуется найти самую дешёвую смесь.
Пусть  - часть тонны смеси, получаемая от руды 1 рудника;
- часть тонны смеси, получаемая от руды 1 рудника;
 - часть тонны смеси, получаемая от руды 2 рудника;
- часть тонны смеси, получаемая от руды 2 рудника;
 - часть тонны смеси, получаемая от руды 3 рудника;
- часть тонны смеси, получаемая от руды 3 рудника;
 - часть тонны смеси, получаемая от руды 4 рудника;
- часть тонны смеси, получаемая от руды 4 рудника;
Тогда количество элементов А, В, С в одной тонне смеси определяется неравенствами
10  + 3
+ 3  + 8
+ 8  + 2
+ 2 
 5;
5;
90  + 150
+ 150  + 75
+ 75  + 175
+ 175 
 100;
100;
45  + 25
+ 25  + 20
+ 20  + 37
+ 37 
 30.
30.
Поскольку сумма четырёх компонентов должна давать 1
 +
+  +
+  +
+  = 1;
= 1;
Это ограничение называется ограничением материального баланса и задаётся в виде равенства.
Целевая функция, определяющая стоимость тонны любой смеси, имеет вид
L = 800  + 400
+ 400  + 600
+ 600  + 500
+ 500 
 min.
min.
Приведя математическое описание к стандартному (для программы Optimization Toolbox) виду, получим
L = 800  + 400
+ 400  + 600
+ 600  + 500
+ 500 
 min.
min.
-10  - 3
- 3  - 8
- 8  - 2
- 2 
 -5;
-5;
-90  - 150
- 150  - 75
- 75  - 175
- 175 
 -100;
-100;
-45  - 25
- 25  - 20
- 20  - 37
- 37 
 -30;
-30;
 +
+  +
+  +
+  = 1;
= 1;

 0;
0; 
 0;
0; 
 0;
0; 
 0.
0.
В рабочем окне программы Matlab выполняем действия, приведенные ниже
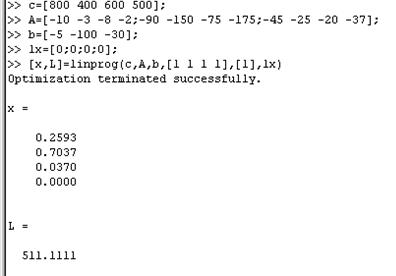 Согласно решению задачи руду из рудника 4 не нужно доставлять в бункер. Минимальная стоимость
Согласно решению задачи руду из рудника 4 не нужно доставлять в бункер. Минимальная стоимость
1 тонны смеси составляет 511$.
| <== предыдущая лекция | | | следующая лекция ==> |
| Иллюстрация экспертного исследования | | | Россия во второй половине XIX века. |
Дата добавления: 2015-10-21; просмотров: 1883;
