Интегрирование по частям
Интегрирование по частям производится по формуле:
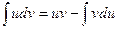 ,
,
Где u и v – функции переменной интегрирования, например х.
Пользуясь формулой интегрирования по частям, необходимо соблюдать требование, чтобы dx обязательно входило в состав dv и чтобы через dv была обозначена такая функция, интеграл которой можно легко найти.
Например,
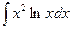 .
.
Решение. Положим u=lnx, dv= x2dx, откуда (дифференцируя u и интегрируя dv)
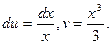
Постоянная С в этом случае не ставится; она будет поставлена в окончательном результате, когда будет найден данный интеграл.
Обращаемся теперь к формуле интегрирования по частям:
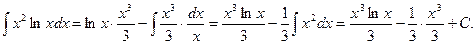
Дата добавления: 2015-10-13; просмотров: 502;
