Квадратичная форма отрицательно определена тогда и только тогда, когда , ,…, .

Доказательство:

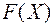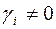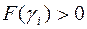Необходимость. Дано, что – положительно определенная форма. Так как , то и поэтому .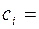

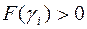Достаточность. Дано, что в каноническом виде все коэффициенты 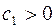, ,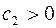…, 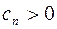.Нужно доказать, что 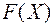положительно определена. Рассмотрим произвольный ненулевой вектор 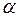и разложим его по базису :

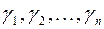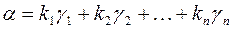
Так как 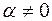, то в разложении 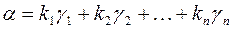не все коэффициенты равны нулю. Следовательно 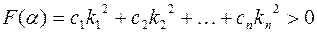, так как 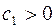, ,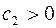…, 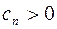и среди чисел 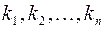хотя бы одно отлично от нуля.

Аналогично доказывается и второе утверждение.

Эта теорема дает два наиболее употребляемых критерия положительной и отрицательной определенности квадратичной формы.

Теорема. Дана квадратичная форма 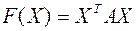. Тогда справедливы следующие утверждения: