Относительная частота

Относительная частота, наряду с вероятностью, принадлежит к основным понятиям теории вероятностей.

Определение 2.3. Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний, т.е.

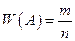. (2.3)

где m –число появлений события, n – общее число испытаний.

Пример 2.5. По цели производится 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели

.

,

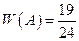Сопоставляя определения вероятности и относительной частоты, заключаем: определение вероятности не требует, чтобы испытания производились в действительности; определение же относительной частоты предполагает, что испытания были произведены фактически. Поэтому вероятность события является априорной (доопытной) характеристикой, а относительная частота – это апостериорная (послеопытная) характеристика.

Длительные наблюдения показали, что если в одинаковых условиях производятся опыты, в каждом из которых число испытаний достаточно велико, то относительная частота обнаруживает свойство устойчивости. Это свойство состоит в том, что в различных опытах относительная частота изменяется мало (тем меньше, чем больше произведено испытаний), колеблясь около некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события.

Таким образом, если опытным путем установлена относительная частота, то полученное число можно принять за приближенное значение вероятности.

Как уже отмечалось выше, классическое определение вероятности предполагает, что число элементарных исходов испытания – конечно. На практике же весьма часто встречаются испытания, число возможных исходов которых – бесконечно. В таких случаях классическое определение неприменимо. Уже это обстоятельство указывает на ограниченность классического определения. Правда, указанный недостаток может быть преодолен путем соответствующего обобщения определения вероятности.

Наиболее слабая сторона классического определения состоит в том, что очень часто невозможно представить результат испытания в виде совокупности элементарных событий. Еще труднее указать основания, позволяющие считать элементарные события равновозможными. Обычно о равновозможности элементарных исходов испытания заключают из соображения симметрии.

3. ТЕОРЕМЫ СЛОЖЕНИЯ И УМНОЖЕНИЯ

ВЕРОЯТНОСТЕЙ