Основные свойства пределов
1. Функция не может иметь более одного предела (при одной и той же базе).
2. Предел постоянной равен самой этой постоянной: 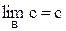 , с – постоянная.
, с – постоянная.
3. Предел суммы функций равен сумме пределов этих функций: 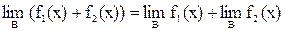
4. Предел произведения функций равен произведению пределов этих функций: 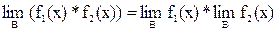
Отсюда следует, что постоянный множитель можно выносить за знак предела: 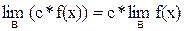
5. Предел частного двух функций равен частному пределов этих функций (если предел делителя не равен нулю): 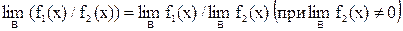
6. (свойство предела сложной функции) Если 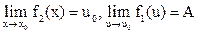 , то предел сложной функции
, то предел сложной функции 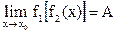 .
.
7. Если при базе В (т.е. в некоторой окрестности точки х0 или при достаточно больших х) f1(х) < f2(х), то 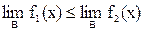 .
.
Отметим, что в перечисленных свойствах предполагается существование пределов функций f1(х) и f2(х), из чего следуют заключения о значениях пределов суммы, произведения или частного этих функций. Но при этом из существования предела суммы, произведения или частного функций не обязательно следует, что существуют пределы самих слагаемых, сомножителей или делимого и делителя.
Например, 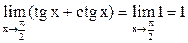 , но при этом
, но при этом 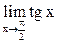 не существует.
не существует.
Дата добавления: 2015-10-06; просмотров: 890;
