I. ОБЩАЯ ТЕОРИЯ МНОЖЕСТВ

В.1. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:

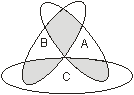
2. Построить взаимно однозначное отображение множества натуральных чисел N на множество рациональных чисел из интервала [0,2].

В.2. 1. Доказать по методу математической индукции, что:

1 + 4 + 7 + … + (3n - 2) = n·(3n - 1)/2.

2. Доказать второй закон де Моргана алгебры множеств.

В. 3. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой В D (A Ç ØВ È С).

2. Привести на множестве Х = {0,1} примеры двух отношений:

а) антирефлексивного и симметричного,

б) не рефлексивного, не антирефлексивного, но антисимметричного.

В. 4.1. Доказать по методу математической индукции, что при любых натуральных n справедливо: 4²ⁿ +5ⁿ –1кратно 20.

2. Проверить (доказать или опровергнуть), будет ли формула (А D В) Í(А\В) теоремой алгебры множеств.

В. 5. 1 Проверить (доказать или опровергнуть), будет ли формула (A Ç B)Í Ø(А D B)теоремой алгебры множеств.

2. Проверить, будет ли отношением эквивалентности на множестве натуральных чисел N отношение, задаваемое предикатом Р(х, у)=” х²+ у²= 25“.

В. 6. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:

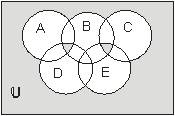
2. Привести собственный пример множеств А и В и отображения f : A® B, которое является сюръективным, но не инъективным. Ответ обосновать.

В. 7. 1. Доказать по методу математической индукции, что при любых натуральных n выражение 2²ⁿ +3^{2n -}1кратно 6.

2. Проверить (доказать или опровергнуть), будет ли формула (A D B) Í Ø А È Ø В теоремой алгебры множеств.

В. 8. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:

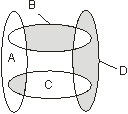
2. Доказать эквивалентность множества точек трехмерного шара единичного диаметра и множества точек куба с единичной длиной ребер.

В.9.1. Привести пример формул составных множеств F₁(А,В,С), F₂(А,В,С)таких, что равенство F₁(А,В,С) = F₂(А,В): а) выполняется для попарно непересекающихся исходных множеств А, В, С иб) не выполняется для пересекающихся А,В,С .

2. Найти мощность множества точек на одном витке спирали c радиусом R и шагом Р, задаваемом параметрическим уравнением:

x = Rsint, y = Rcost, z = Pt, 0 £ t £ 2p.

В. 10. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой Ø А Ç ВD( A È (С\В)).

2. Ввести отношения а) строгого и б) нестрогого порядка на множестве векторов на евклидовой плоскости. Исследовать линейность порядков, наличие наименьшего и наибольшего элементов.

В. 11. 1. Привести примеры непустых множеств А, В и С, для которых формула А È В È С = С : а) справедлива и б) несправедлива.

2. Найти мощность точек плоскости, ограниченное эллипсом 4х²+у²=1.

В. 12.Можно ли придумать пример множества А, для которого не выполняется закон исключения третьего? Ответ обосновать.

2. Будут ли задавать отношение эквивалентности на множестве натуральных чисел N предикаты: а) Р(х,у)=”х - у =1“, б) Q(х,у)=”х - у =0“.

В.13. 1. Доказать по методу математической индукции, что при любых натуральных n справедливо: 0 + 2 + 6 + … +(n² - n) = n·(n² -1)/3.

2. Можно ли построить взаимно однозначное отображение множества чётных натуральных чисел N₂ на множество вещественных чисел из интервала [0; 0,1] ? Ответ обосновать.

В. 14. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой (B\A) È (С Ç А\B).

2. Привести пример отображения на множестве геометрических фигур, которое однозначно, но не взаимно однозначно.

В.15. 1. Привести пример непустых множеств А,В,С, для которых (А¹В, А¹С, В¹С) и одновременно справедливы формулы А Ç В Ç С = С , А È В È С = А .

2. Проверить (доказать или опровергнуть), будет ли формула A\B Í ØA теоремой алгебры множеств.

В. 16. 1. Доказать по методу математической индукции, что разность 3²ⁿ -5ⁿ при любых натуральных n ³ 2 кратна 4.

2. Ввести отношение частичного порядка на множестве квадратичных парабол на плоскости, задаваемых формулой у = ах² + bx + c .Исследовать линейность порядка, наличие наименьшего и наибольшего элементов.

В. 17. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой Ø (А Ç В )È С.

2. Заданы множества Х = {D, , O} и Y = {a, b, c}. Построить декартовы произведения Х´ Y, Y´ Х и декартов квадрат Х².

В. 18. 1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:

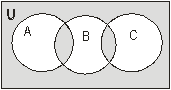
2. Доказать справедливость для любых множеств А и В следующего соотношения: если А Í В, то Ø В Í Ø А.

В. 19. 1. Проверить (доказать или опровергнуть), будет ли формула (А Ç В) Í А теоремой алгебры множеств.

2. Привести пример взаимно однозначного отображения множества натуральных чисел N на декартов квадрат N ² .

В. 20. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой ВD (A È С ÇØ В).

2. Можно ли построить взаимно однозначное отображение множества вещественных чисел из [0; 1] на множество рациональных чисел из интервала [-¥; + ¥]? Ответ обосновать.

В.21. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой А Ç (В È Ø С).

2. Привести на множестве Х = {А, B, C, D} пример отношения, которое рефлексивно, симметрично, но не транзитивно.

В. 22.1. Доказать по методу математической индукции, что при любых натуральных n справедливо неравенство:

1² + 3² + 5² + 7² +…+(2n-1)²£ n× (2n-1) × (2n+1)/3.

2. На декартовом квадрате множества Х = {0; 1; 2} задать при помощи предиката отношение эквивалентности, разбивающее Х²на два класса эквивалентности.

В. 23.1. Выразить с помощью теоретико-множественных операций в виде формулы заштрихованное множество на диаграмме Венна:

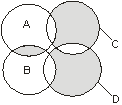
2. Привести примеры непустых множеств А и В, для которых формула Ø А È В = Ø А: а) выполняется и б) не выполняется.

В. 24. 1. Привести пример двух формул составных множеств F₁(А, В, С), F₂(А, В, С)таких, что: а) для попарно непересекающихся исходных множеств А, В, С выполняется равенство F₁(А, В, С)= F₂(А, В, С) , б) для пересекающихся А, В, С выполняется строгое включение F₁(А, В, С) Ì F₂(А,В,С) .

2. Привести собственный пример множеств А и В и отображения f : A® B, которое является инъективным, но не сюръективным. Ответ обосновать.

В. 25.1. Для множеств Х = {α, b, g} и Y = {1; 2; 3; 4}. Построить следующие декартовы произведения: Х´ Y, Y´ Х, Х³и Y².

2. Найти мощность множества точек на гиперболе у = 1/(х-2) при хÎ (3; +¥).

В. 26. 1. Изобразить на полной диаграмме пересечений Венна множество, задаваемое формулой Ø (А D B ) D С .

2. Привести на множестве Х = {D, , O} пример отношения, которое антирефлексивно и не транзитивно.

В. 27. 1.Проверить, будут ли приведенные ниже записи формулами алгебры множеств: а) А D ВÍ А È Ç В, б) (B ØС) =A,в) А Ç В Í В. Ответ обосновать.

2. Проверить справедливость аксиом для отношения на множестве Х = {0; 1; 2; 3}, заданного таблицей