К однородным
Дифференциальное уравнение вида
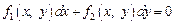 (22.7)
(22.7)
называют однородным, если обе функции 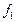 и
и 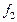 являются однородными функциями одной и той же степени n, т. е. для параметра t выполняются:
являются однородными функциями одной и той же степени n, т. е. для параметра t выполняются: 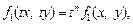
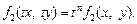
Однородное уравнение может быть сведено к виду
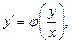 (22.8)
(22.8)
где 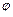 – некоторое выражение относительно
– некоторое выражение относительно 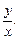
Для решения однородного уравнения его сводят вначале к виду (22.8), а затем заменяют 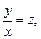 где
где 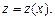 Этой заменой дифференциальное уравнение (22.8) приводится к уравнению с разделяющимися переменными. Иногда целесообразнее сделать замену
Этой заменой дифференциальное уравнение (22.8) приводится к уравнению с разделяющимися переменными. Иногда целесообразнее сделать замену 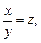 где
где 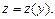
Дифференциальное уравнение вида
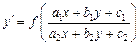 (22.9)
(22.9)
при определенных значениях 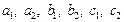 сводится к однородному уравнению. Рассмотрим три возможных случая коэффициентов:
сводится к однородному уравнению. Рассмотрим три возможных случая коэффициентов:
1. Если 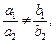 то делают замену переменных:
то делают замену переменных:
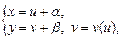 (22.10)
(22.10)
где числа 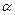 и
и 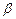 находят как решение системы уравнений
находят как решение системы уравнений
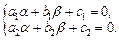 (22.11)
(22.11)
Этой заменой дифференциальное уравнение (22.9) сводится к уравнению
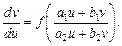
Далее его решают как однородное.
2. Если 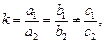 то уравнение (22.9) записывают в виде
то уравнение (22.9) записывают в виде
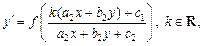
и затем заменяют 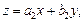 где
где 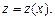 Эта замена приводит к дифференциальному уравнению с разделяющимися переменными.
Эта замена приводит к дифференциальному уравнению с разделяющимися переменными.
3. Если 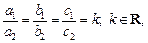 то имеем
то имеем
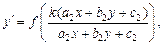
т. е. 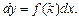 Далее интегрируют.
Далее интегрируют.
Пример 1. Решить уравнение:
1) 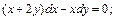 2)
2) 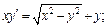
3) 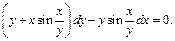
Решение. 1) 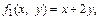
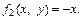 Так как
Так как
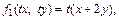
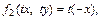
то 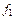 и
и 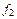 – однородные функции первой степени.
– однородные функции первой степени.
Делаем замену. Очевидно, что делением на 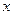
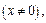 уравнение сводится к виду
уравнение сводится к виду 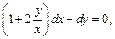 т. е.
т. е. 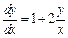 или
или 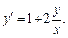 Заменяем
Заменяем 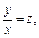 где
где 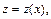 откуда
откуда 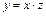 и
и 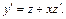 Подставляя в исходное дифференциальное уравнение, получаем:
Подставляя в исходное дифференциальное уравнение, получаем: 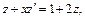 т. е.
т. е. 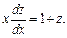
Разделяем переменные (при условии 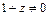 ):
): 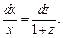 Интегрируем:
Интегрируем: 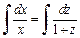 или
или 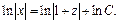 Отсюда
Отсюда 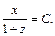
Возвращаемся к старым переменным, подставляем вместо z выражение 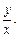 Тогда общий интеграл исходного дифференциального уравнения имеет вид:
Тогда общий интеграл исходного дифференциального уравнения имеет вид: 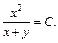
Рассмотрим отдельно возможные решения 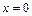 и
и 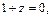 которые мы исключали. В последнем случае имеем
которые мы исключали. В последнем случае имеем 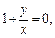 т. е.
т. е. 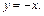 Подставляем
Подставляем 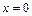 и
и 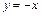 в заданное дифференциальное уравнение и убеждаемся, что они также являются его решениями. При этом решение
в заданное дифференциальное уравнение и убеждаемся, что они также являются его решениями. При этом решение 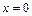 содержится в формуле общего интеграла при
содержится в формуле общего интеграла при 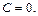 Решение
Решение 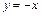 не содержится в полученной формуле общего интеграла. Поэтому окончательное решение:
не содержится в полученной формуле общего интеграла. Поэтому окончательное решение: 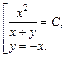
2) Разделив дифференциальное уравнение на x 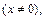 получаем:
получаем: 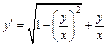 – это однородное дифференциальное уравнение. После замены
– это однородное дифференциальное уравнение. После замены 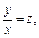 где
где 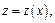 имеем
имеем 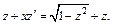
Далее приводим подобные и разделяем переменные, считая 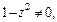 т. е.
т. е. 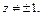 Получаем
Получаем 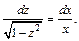 Интегрируем и получаем
Интегрируем и получаем 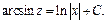
Возвращаемся к старым переменным, получаем общее решение:
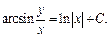
Анализируем, являются ли решениями 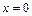 и
и 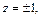 т. е.
т. е. 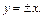 Подставляем
Подставляем 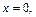
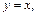
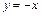 в заданное дифференциальное уравнение и убеждаемся, что
в заданное дифференциальное уравнение и убеждаемся, что 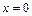 не является решением заданного дифференциального уравнения, а
не является решением заданного дифференциального уравнения, а 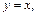
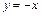 являются решениями, которые не входят в полученное общее решение. Приходим к решению исходного дифференциального уравнения:
являются решениями, которые не входят в полученное общее решение. Приходим к решению исходного дифференциального уравнения:
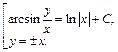
3) Запишем заданное уравнение в виде
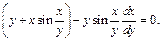
Делим его на y 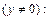
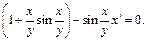 (22.12)
(22.12)
Делаем замену 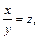 где
где 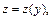 т. е.
т. е. 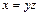 и
и 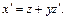 После подстановки в уравнение (22.12) получаем:
После подстановки в уравнение (22.12) получаем:
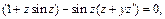 т. е.
т. е.
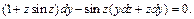
После упрощения имеем 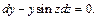
Делим переменные: 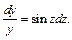
Интегрирование дает:
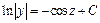 или
или 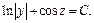
Возвращаемся к старым переменным, используя 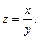 Тогда общий интеграл имеет вид:
Тогда общий интеграл имеет вид: 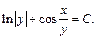
Пример 2. Решить задачу Коши:
1) 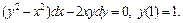
2) 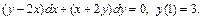
Решение. 1) Это однородное уравнение. Разделив заданное уравнение на 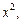
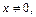 получаем:
получаем:
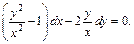
Делаем замену 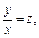
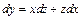 где
где 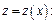
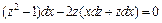
или, приведя подобные,
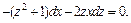
Разделяем переменные:
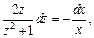
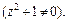
Интегрируем последнее уравнение:
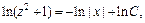
т. е., используя свойства логарифма, имеем 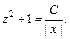
Возвращаясь к старым переменным, получаем: 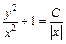 – общий интеграл исходного уравнения.
– общий интеграл исходного уравнения.
Подставляем в него начальные условия 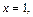
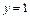 и находим С:
и находим С:
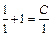 или
или 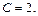
Значит, решением задачи Коши является
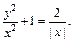
2) Это уравнение однородное. Разделив его на x 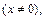 получаем:
получаем:
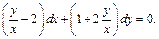
Делаем замену 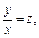 где
где 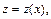
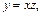
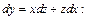
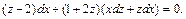
Приводим подобные:
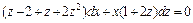 или
или
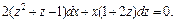
Разделяем переменные, считая 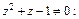
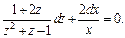 (22.13)
(22.13)
Далее интегрируем уравнение (22.13) и получаем:
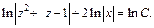
Используем свойства логарифма и получаем: 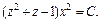
Возвращаемся к старым переменным:
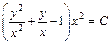 или
или 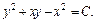
Отсюда получаем:
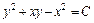 – общий интеграл заданного уравнения. Подставив в него начальные условия:
– общий интеграл заданного уравнения. Подставив в него начальные условия: 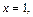
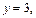 получим
получим 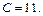
Решение задачи Коши: 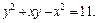
Пример 3. Найти решение дифференциального уравнения:
1) 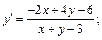 2)
2) 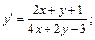 3)
3) 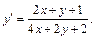
Решение. 1) Это уравнение не является однородным, но сводится к однородному дифференциальному уравнению. Так как 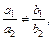 т. е.
т. е. 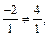 сделаем замену переменных по формуле (22.10):
сделаем замену переменных по формуле (22.10):
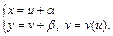 (22.14)
(22.14)
Числа 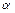 и
и 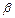 найдем из системы уравнений (22.11):
найдем из системы уравнений (22.11):
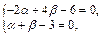 откуда
откуда 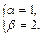
Тогда система уравнений (22.14) примет вид 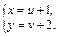
Подставив эту замену в заданное уравнение, получим:
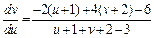 или
или
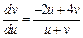 – однородное дифференциальное уравнение.
– однородное дифференциальное уравнение.
Сделаем замену переменных: 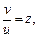 где
где 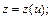
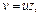
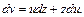 Подставив ее в последнее уравнение, получим:
Подставив ее в последнее уравнение, получим:
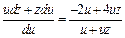 или
или
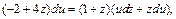
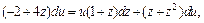
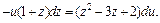
Разделим переменные, полагая 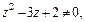 получим:
получим:
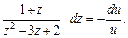
Преобразуем дробное выражение 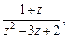 представив его в виде суммы простейших дробей:
представив его в виде суммы простейших дробей: 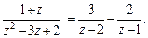
Тогда получаем:
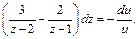
Интегрируем последнее уравнение:
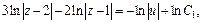
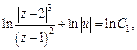
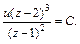
Возвращаемся к старым переменным:
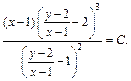
После упрощения получаем: 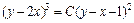 – общий интеграл заданного дифференциального уравнения.
– общий интеграл заданного дифференциального уравнения.
Кроме того, решением исходного дифференциального уравнения будет 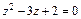 или
или 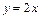 и
и 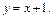
Решение 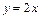 входит в общий интеграл при С = 0. Таким образом, искомое решение дифференциального уравнения
входит в общий интеграл при С = 0. Таким образом, искомое решение дифференциального уравнения
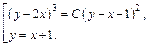
2) Так как 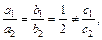 то заданное уравнение приводится к уравнению
то заданное уравнение приводится к уравнению 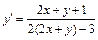 .
.
Заменяем 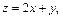 где
где 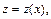
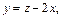
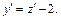
Получим: 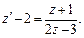
Разделяем переменные:
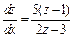 или
или 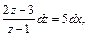 (считаем
(считаем 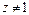 ), т. е.
), т. е.
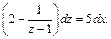
Интегрируем:
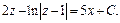
Возвращаемся к старым переменным и получаем общий интеграл:
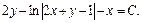
Кроме того, решением исходного дифференциального уравнения будет 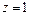 или
или 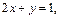 т. е.
т. е. 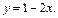 Таким образом, искомое решение дифференциального уравнения:
Таким образом, искомое решение дифференциального уравнения:
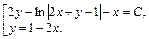
3) Так как 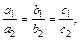 т. е.
т. е. 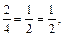 то заданное уравнение сводится к уравнению
то заданное уравнение сводится к уравнению
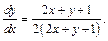
После сокращения имеем 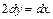 Интегрируем и получаем общее решение исходного дифференциального уравнения:
Интегрируем и получаем общее решение исходного дифференциального уравнения: 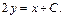
Дата добавления: 2015-09-29; просмотров: 801;
