Методы интегрирования. 1. Непосредственное интегрирование основано на свойствах интеграла, формуле Ньютона-Лейбница и таблице интегралов.
1. Непосредственное интегрирование основано на свойствах интеграла, формуле Ньютона-Лейбница и таблице интегралов.
2. Замена переменной:
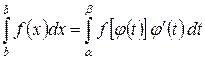 ,
,
где 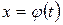 – функция, непрерывная вместе со своей производной
– функция, непрерывная вместе со своей производной 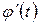 на отрезке
на отрезке 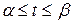 ,
, 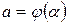 ,
, 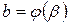 ,
, 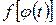 – функция, непрерывная на
– функция, непрерывная на 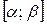 . После вычисления последнего интеграла нет необходимости возвращаться к прежней переменной
. После вычисления последнего интеграла нет необходимости возвращаться к прежней переменной 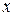 .
.
3. Интегрирование по частям:
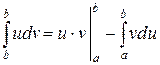 ,
,
где 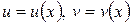 – непрерывно дифференцируемые функции на отрезке
– непрерывно дифференцируемые функции на отрезке 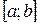 . Все рекомендации относительно обозначений
. Все рекомендации относительно обозначений 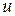 и
и 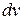 сохраняются.
сохраняются.
Пример. Вычислить интеграл 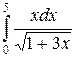 .
.
Решение. Вводим новую переменную интегрирования, полагая 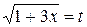 . Отсюда находим
. Отсюда находим 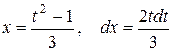 и новые пределы интеграла:
и новые пределы интеграла: 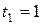 при
при 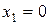 ,
, 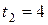 при
при 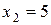 .
.
Подставляя, получим
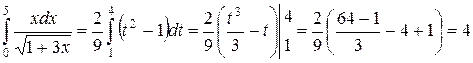 .
.
Пример. Вычислить интеграл 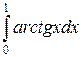 .
.
Решение. По формуле интегрирования по частям находим
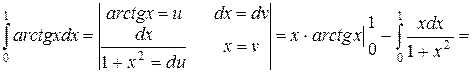
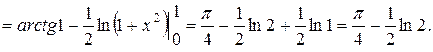
| 6. Несобственный интеграл |
Несобственными интегралами называются:
§ интегралы с бесконечными пределами от ограниченных функций;
§ интегралы с конечными пределами от неограниченных функций.
Несобственный интеграл от функции 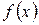 в переделах от
в переделах от 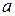 до
до 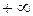 определяется равенством
определяется равенством
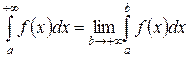 .
.
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся; если же предел не существует или равен бесконечности – расходящимся.
Аналогично
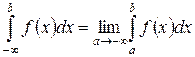 ,
,
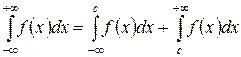 ,
,
где 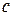 – произвольная точка.
– произвольная точка.
Если функция 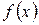 не ограничена в окрестности точки
не ограничена в окрестности точки 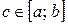
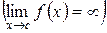 , и непрерывна при
, и непрерывна при 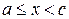 и
и 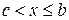 , то, по определению, полагают
, то, по определению, полагают
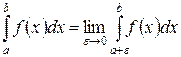
| 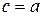
|
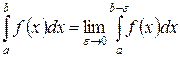
| 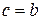
|
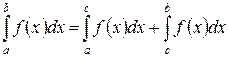
| 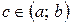
|
Несобственный интеграл 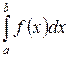 называется сходящимся, если оба предела конечны в правой части равенства, и расходящимся, если не существует или равен бесконечности хотя бы один из них.
называется сходящимся, если оба предела конечны в правой части равенства, и расходящимся, если не существует или равен бесконечности хотя бы один из них.
Пример. Вычислить несобственный интеграл 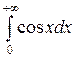 .
.
Решение. Имеем
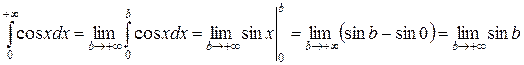 ,
,
предел не существует, следовательно, интеграл расходится.
Пример. Вычислить 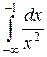 .
.
Решение. Найдем
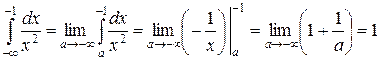 ,
,
несобственный интеграл сходится.
Пример. Найти 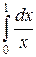 .
.
Решение. Подынтегральная функция 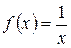 в точке
в точке 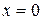 неограниченна, поэтому
неограниченна, поэтому
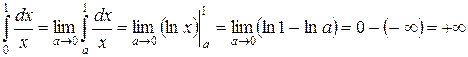 ,
,
т.е. несобственный интеграл расходится.
| 7. Дифференциальные уравнения |
Дифференциальным уравнением называется соотношение, связывающее независимую переменную, неизвестную функцию и ее производные (или ее дифференциалы).
Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящий в уравнение.
Дифференциальное уравнение порядка 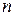 в общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до порядка
в общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до порядка 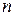 включительно и имеет вид
включительно и имеет вид
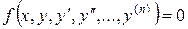 .
.
Дифференциальное уравнение первого порядка имеет вид
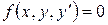 .
.
Задача состоит в определении из дифференциального уравнения неизвестной функции, а процесс определения функции называется интегрированием дифференциального уравнения.
Решением уравнения первого порядка называется всякая дифференцируемая функция 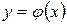 , удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение оно обращается в тождество
, удовлетворяющая этому уравнению, т.е. такая, после подстановки которой в уравнение оно обращается в тождество
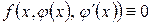 .
.
Кривая 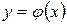 , определяемая решением уравнения называется интегральной кривой дифференциального уравнения.
, определяемая решением уравнения называется интегральной кривой дифференциального уравнения.
Общим решением дифференциального уравнения первого порядка называется соотношение вида
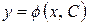 ,
,
содержащее произвольную постоянную и являющееся решением дифференциального уравнения при любом действительном значении постоянной 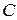 .
.
Иногда вместо общего решения получают общий интеграл
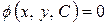 ,
,
где 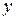 – функция переменной
– функция переменной 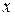 .
.
Уравнения 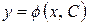 определяют семейство интегральных кривых уравнения первого порядка.
определяют семейство интегральных кривых уравнения первого порядка.
Частным решением дифференциального уравнения называется такое решение, которое получается из общего решения при некотором частном значении произвольной постоянной.
Дата добавления: 2015-09-28; просмотров: 655;
