Кривая нормального распределения

Большинство процедур статистического анализа, часто используемых в исследованиях, основаны на предположении о том, что наблюдаемые переменные распределяются среди всей популяции по нормальному закону. Если переменная имеет нормальное распределение, то при графическом представлении данных большого числа измерений этой переменной получится кривая характерной колоколообразной формы, которая называется кривой нормального распределения (ее часто называют просто нормальной кривой). Если, например, измерить рост (переменная) большого числа мужчин и женщин, случайно выбранных однажды утром из толпы прохожих на углу живленной улицы, то в этой выборке окажется относительно небольшая процентная доля очень высоких и очень низкорослых людей. Большинство людей из выборки будут иметь средний рост. В графической форме эту серию наблюдений можно представить в виде кривой нормального распределения, изображенной на рис. 2.2.

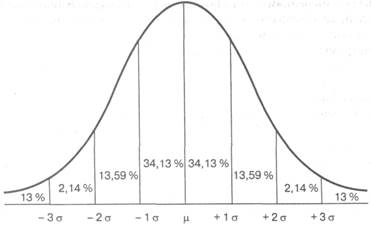
Рис. 2.2. Кривая нормального распределения

Естественно происходящие события, такие как забастовки, дают индустриально-организационным психологам возможность проведения полезных полевых и обсервационных исследований.

Любую нормальную кривую можно описать с помощью двух чисел. Одно из них — это усредненное по всем измерениям значение переменной, выраженное в единицах используемой шкалы, то есть среднее значение (m) распределения. Как показано на рис. 2.2, точка с абсциссой m лежит на оси симметрии кривой. Второе число, описывающее нормальную кривую, характеризует вариабельность, или разброс точек кривой относительно среднего значения. С помощью математических преобразований вариабельность всех кривых такого вида можно выразить через стандартную единицу, которая называется стандартным отклонением (s).

Если известны среднее значение и стандартное отклонение нормальной кривой, то любой человек может точно воспроизвести эту кривую, поскольку при нормальном распределении переменной в каждый интервал длиной в одно стандартное отклонение влево или вправо от среднего значения попадает строго определенная процентная доля всех наблюдавшихся значений переменной. Эти процентные доли указаны на рис. 2.2: например, 68,26 % всех значений переменной отличаются от среднего значения не более чем на одно стандартное отклонение (по 34,13 % в меньшую и в большую стороны).

Кривая нормального распределения не только служит основой формального статистического анализа, но и используется в некоторых других целях. Одна из наиболее важных целей — объяснить людям, что означают баллы, полученные ими при прохождении тестов. Если среднее значение результатов стандартизованного теста математических способностей равно 50 баллам, а стандартное отклонение — 10, то человек, получивший, например, 70 баллов, справился с тестом лучше, чем примерно 95 % людей, которые проходили этот тест. Результат 70 баллов на два стандартных отклонения превышает средний (50 + 10 + 10 = 70).

Большинство статистических процедур основаны на предположении о нормальности кривой распределения, но некоторые важные для исследования переменные не подчиняются нормальному закону распределения. Такая переменная, как пол, имеет бимодальное распределение, то есть при измерении она может принимать только два значения — мужской и женский. Другие переменные имеют так называемое асимметричное распределение, когда большинство значений переменной группируется вокруг точки измерительной шкалы, которая не является средним значением. Асимметричное распределение имеет вес тела американцев; для людей любого роста и пола (то есть при условии контроля над ростом и полом) доля людей с весом выше среднего больше, чем доля людей с весом ниже среднего.

Для анализа переменных, имеющих бимодальное, асимметричное и другие отличные от нормального распределения, необходимы специальные статистические процедуры, но за немногими исключениями (например, пол) эти переменные редко встречается в индустриально-организационной психологии. Однако распределение данных наблюдений для конкретной выборки может отличаться от не нормального из-за особенностей плана эксперимента или ошибок при формировании выборки.