Порядок выполнения работы. Задание I. Определение коэффициента упругости пружин
Задание I. Определение коэффициента упругости пружин
1. Подвесьте пружины с помощью балки 17 на оси блока 13 и закрепите на другом конце пружин груз т1(см. рис. 2).
2. Измерьте линейкой расстояние x1от основания стойки до нижнего края груза.
3. Измените массу груза на величину Δm и измерьте новое расстояние х2. Данные занесите в табл. 1. Рассчитайте коэффициент упругости пары пружин по формуле
 (18)
(18)
где g = 9,81 м/с – ускорение свободного падения.
4. Повторите измерения несколько раз. Рассчитайте среднее значение kпар . Данные занесите в табл. 1.
Таблица 1
| № п/п | т1 | m2 | 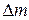 =т1– m2, кг =т1– m2, кг
| x1 | х2 | Δх=х2 – х1, м | kпар, Н/м |
| … | |||||||
| Среднее | – | ― | - | - |
Задание II.Определение момента инерции методом
крутильных колебаний
1. Подготовьте измерительную систему ИСМ-1 к работе: подключите датчик угла поворота стола блока к разъему №1на задней стенке прибора, переключатель 1 поставьте в положение «К1», переключатель 4 – в положение «2», переключатель 5 – в положение «цикл», переключатель 8 – в положение «+» или переключатель 9 – в среднее положение. Включите питание модуля.
2. Накрутите нить (1,5 оборота) на шкив стола, диаметр которого D = 50мм (рис. 3), прикрепите к концам нити пружины. Закрепите пружины на осях 12 нижнего блока стойки 10.
3. Поверните стол так, чтобы в свободном положении указатель угла поворота стола находился вблизи нулевого деления шкалы 16.
4.
 |
Нажмите кнопку 7 «готов» и приведите стол в колебательное движение с амплитудой 40 – 60 градусов.
Рис.3. Определение момента инерции маятника
5. Считайте с индикатора время одного полного колебания T.
 6. Рассчитайте момент инерции ненагруженного стола по формуле
6. Рассчитайте момент инерции ненагруженного стола по формуле
(19)
где R – радиус шкива стола (R=D/2), kпар – коэффициент упругости двух пружин, соединенных параллельно. Данные занесите в табл. 2. Повторите измерения 5 – 7 раз.
Таблица 2
| № п/п | Т (c) | Io ,кг м2 |
| … | ||
| среднее |
Задание III.Проверка теоремы Штейнера
1. Поместите в центре стола два цилиндрических груза 18 массой тцпо 500 г один над другим (точная масса грузов выгравирована на нижнем торце грузов). Повторите измерения момента инерции системы Iсис (по п. 3 – 6 в задании II).
2. Рассчитайте момент инерции цилиндров по формуле
Iц = Iсис – Iо , (21)
где I0 - момент инерции не нагруженного стола, измеренный в задании II.
3. Рассчитайте теоретический момент инерции цилиндров Iтеор относительно оси цилиндров по формуле
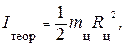 (22)
(22)
где тц – суммарная масса цилиндров, Rц – радиус цилиндров
(Rц = 24 мм). Данные занесите в табл. 3.
4. Переместите цилиндры на одинаковое расстояние Δх относительно оси вращения (шаг отверстий на вращающемся столе Δх=20мм).Измерьте период колебаний m2 системы, соответствующий новому положению цилиндров. Данные занесите в табл. 3.
Таблица 3
| № п/п | Δх | Δх2 | Tсис | Tсис2 | тц = т1+ m2 | Iсис | Iо | Iтеор |
| … |
5. Рассчитайте момент инерции системы Iсис по формуле
 (23)
(23)
где kпар – коэффициент упругости пары пружин (см. задание I),
R –- радиус шкива стола.
 6. Рассчитайте теоретический момент инерции системы по формуле
6. Рассчитайте теоретический момент инерции системы по формуле
где I0 – момент инерции не нагруженного стола (см. задание II), тц – суммарная масса цилиндров, Rц – радиус цилиндров
(Rц = 24 мм).
7. Повторите измерения и расчеты по п. 1– 6 для всех положений цилиндров. Данные занесите в табл. 3.
8. Постройте график зависимости момента инерции Iсиси Iтеор от квадрата расстояния от оси вращения до центра грузов Δх2.
Контрольные вопросы
1. Дайте определение динамических характеристик вращательного движения: момента силы – М, момента инерции – I, момента импульса – L.
2. Запишите аналитические выражения для момента инерции частицы и твердого тела. Как производится расчет момента инерции обруча, стержня, диска?
3. В чем состоит суть теоремы Штейнера?
4. Получите основное уравнение динамики вращательного движения.
5. Получите уравнение колебаний крутильного маятника.
6. Как рассчитать период колебаний крутильного маятника?
Дата добавления: 2015-09-18; просмотров: 656;
